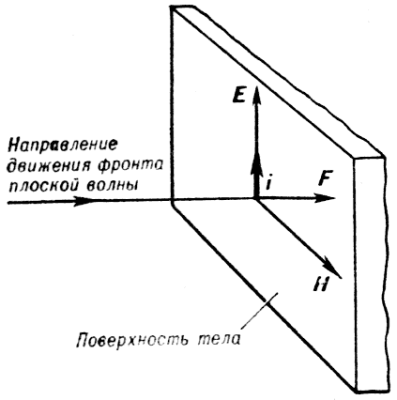
- •3. Свойства электромагнитных волн. Шкала электромагнитных волн. Применение электромагнитных волн.
- •8.Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля.
- •9. Дифракция Френеля на круглом отверстии и диске, описание дифракционных картин.
- •10. Дифракция Фраунгофера на прямоугольном отверстии и дифракционной решетке, условия максимумов и минимуиов, распределение интенсивности в дифракционной картине.
- •11. Основные характеристики спектральных приборов. Дисперсия: линейная и угловая, разрешающая способность оптических приборов, критерий Рэлея.
- •Линейная дисперсия ,
- •12.Поляризация света; естественный, частично поляризованный и поляризованный свет; состояние поляризации.
- •13. Поляризаторы. Закон Малюса. Степень поляризации.
- •14. Поляризация света при отражении и преломлении. Закон Брюстера.
- •15. Двойное лучепреломление. Поляризационные устройства. Интерференция поляризованного света.
- •16.Дисперсия света; нормальная и аномальная дисперсия; классическая электронная теория дисперсия.
- •17. Поглощение света, закон Бугера.
- •18.Корпускулярно-волновая двойственность свойств электромагнитного излучения, связь между волновыми и квантовыми характеристиками.
- •19. Давление излучения. Объяснение давления с точки зрения волновой и квантовой теорий.
- •20.Корпускулярно-волновая двойственность свойств вещества, гипотеза де Бройля, свойства волн де Бройля.
- •21. Тепловое излучение тел и его характеристики.
- •22.Законы теплового излучения. Абсолютно черное тело.
- •23. Фотоэффект: разновидности, законы, вольтамперная характеристика, уравнение Эйнштейна.
- •24.Эффект Комптона: законы сохранения, объяснение с точки зрения квантовой теории.
- •25. Соотношение неопределенностей Гейзенберга.
- •26.Зонная теория твердых тел (внутренний фотоэффект). Проводники, полупроводники и диэлектрики с точки зрения зонной теории.
- •27. Атом водорода. Модели Томсона и Резерфорда. Постулаты Бора.
- •28.Спектр излучения атома водорода. Опыты Франка и Герца. Квантовые числа.
- •29. Спонтанное и вынужденное излучение фотонов. Поглощение фотонов.
- •31. Временное и стационарное уравнение Шредингера. Движение свободной частицы, частица в бесконечно глубокой потенциальной яме.
19. Давление излучения. Объяснение давления с точки зрения волновой и квантовой теорий.
Давление
излучения -
давление, оказываемое электромагнитным
излучением на тела, взаимодействующие
с ним. В физике давление определяется
как сила, действующая на единичную
площадку по направлению нормали к
площадке, или как импульс, переносимый
за ед. времени через единичную площадку
по направлению нормали к ней. Объяснение
Д. и. может быть дано на основе как
волновых, так и квантовых представлений
о природе излучения. Излучение можно
рассматривать как совокупность фотонов
(квантов эл.-магн. поля). Каждый фотон
обладает энергией ![]() и
импульсом
и
импульсом ![]() .
При поглощении фотона его импульс
передаётся поглощающему телу. При
рассеянии излучения частицы вещества
также получают импульс от фотонов.
Согласно закону сохранения импульса,
Д. и. испытывают и тела испускающие
фотоны.
.
При поглощении фотона его импульс
передаётся поглощающему телу. При
рассеянии излучения частицы вещества
также получают импульс от фотонов.
Согласно закону сохранения импульса,
Д. и. испытывают и тела испускающие
фотоны.
|
Вычислим величину светового давления.
На
тело площадью S падает
световой поток с энергией ![]() ,
где N – число
квантов. K
,
где N – число
квантов. K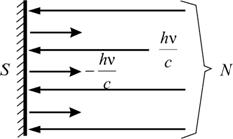 N квантов
отразится от поверхности; (1 – K)N–
поглотится, K–
коэффициент отражения.
N квантов
отразится от поверхности; (1 – K)N–
поглотится, K–
коэффициент отражения.
Каждый
отраженный фотон передаст телу импульс:
![]() ,
т.к.
,
т.к. ![]() .
.
В
единицу времени все N квантов
сообщают телу импульс р:
![]()
Т.к. фотон обладает импульсом, то импульс, переданный телу за одну секунду, есть сила давления – сила, отнесенная к единице поверхности.
Тогда
давление ![]() ,
или
,
или
![]()
где J –
интенсивность излучения. Т. е. давление
света можно рассчитать:
![]()
Если
тело зеркально отражает, то K =
1 и ![]()
Если
полностью поглощает (абсолютно черное
тело), то K =
0 и ![]() ,
т.е. световое
давление на абсолютно черное тело в два
раза меньше, чем
на зеркальное.
,
т.е. световое
давление на абсолютно черное тело в два
раза меньше, чем
на зеркальное.
20.Корпускулярно-волновая двойственность свойств вещества, гипотеза де Бройля, свойства волн де Бройля.
Корпускулярно-волновой дуализм свойств вещества.
Французский ученый Луи де Бройль, развивая представления о двойственной корпускулярно-волновой природе света, выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.
Итак,
согласно де Бройлю, с каждым микрообъектом
связываются, с одной стороны, корпускулярные
характеристики -энергия Е и импульс р,
а с другой — волновые характеристики
— частота ![]() и
длина волны
и
длина волны ![]() .
Количественные соотношения, связывающие
корпускулярные и волновые свойства
частиц, такие же, как для фотонов:
.
Количественные соотношения, связывающие
корпускулярные и волновые свойства
частиц, такие же, как для фотонов:
![]() ,
, ![]() .
.
Свойство:
Для
частиц не очень высокой энергии,
движущихся со скоростью ![]() (скорости
света),
импульс равен
(скорости
света),
импульс равен ![]() (где
(где ![]() —
масса частицы), и
—
масса частицы), и ![]() .
Следовательно, длина волны де Бройля
тем меньше, чем больше масса частицы и
её скорость. Например, частице с массой
в 1 г, движущейся со скоростью 1 м/с,
соответствует волна де Бройля с
.
Следовательно, длина волны де Бройля
тем меньше, чем больше масса частицы и
её скорость. Например, частице с массой
в 1 г, движущейся со скоростью 1 м/с,
соответствует волна де Бройля с ![]() м,
что лежит за пределами доступной
наблюдению области. Поэтому волновые
свойства несущественны в механике
макроскопических тел. Для электронов
же с энергиями от 1 эВ до
10 000 эВ длина волны де Бройля лежит в
пределах от ~ 1 нм до 10−2 нм,
то есть в интервале длин волн рентгеновского
излучения.
Поэтому волновые свойства электронов
должны проявляться, например, при их
рассеянии на тех же кристаллах, на
которых наблюдается дифракция рентгеновских
лучей.
м,
что лежит за пределами доступной
наблюдению области. Поэтому волновые
свойства несущественны в механике
макроскопических тел. Для электронов
же с энергиями от 1 эВ до
10 000 эВ длина волны де Бройля лежит в
пределах от ~ 1 нм до 10−2 нм,
то есть в интервале длин волн рентгеновского
излучения.
Поэтому волновые свойства электронов
должны проявляться, например, при их
рассеянии на тех же кристаллах, на
которых наблюдается дифракция рентгеновских
лучей.