28.Спектр излучения атома водорода. Опыты Франка и Герца. Квантовые числа.

В нагретом до высокой температуры водороде можно наблюдать характерный линейчатый спектр. Все спектральные линии группируются в серии в зависимости от того, на какой энергетический уровень переходят электроны.

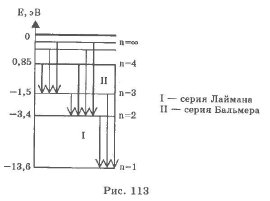
Переходы впервые возбужденные состояния на второй энергетический уровень с верхних уровней образуют серию Бальмера (n = 2), при переходе на первый энергетический уровень с n = 1 образуют серию Лаймана. 

Опыт Франка — Герца — опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома.

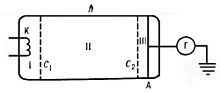
На рисунке приведена схема опыта. К катоду К и сетке C₁ электровакуумной трубки, наполненной парами Hg (ртути), прикладывается разность потенциалов V, ускоряющая электроны, и снимается зависимость силы тока I от V. К сетке C₂ и аноду А прикладывается замедляющая разность потенциалов. Ускоренные в области I электроны испытывают соударения с атомами Hg в области II. Если энергия электронов после соударения достаточна для преодоления замедляющего потенциала в области III, то они попадут на анод. Следовательно, показания гальванометра Г зависят от потери электронами энергии при ударе.

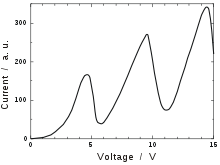
В опыте наблюдался монотонный рост I при увеличении ускоряющего потенциала вплоть до 4,9 В, то есть электроны с энергией Е < 4,9 эВ испытывали упругие соударения с атомами Hg и внутренняя энергия атомов не менялась. При значении V = 4,9 В (и кратных ему значениях 9,8 В, 14,7 В) появлялись резкие спады тока. Это определённым образом указывало на то, что при этих значениях V соударения электронов с атомами носят неупругий характер, то есть энергия электронов достаточна для возбуждения атомов Hg. При кратных 4,9 эв значениях энергии электроны могут испытывать неупругие столкновения несколько раз.

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 доn-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями,  l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),  l = 2 – d-орбиталями (5 типов),  l = 3 – f-орбиталями (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1

29. Спонтанное и вынужденное излучение фотонов. Поглощение фотонов.

Процесс излучения электромагнитной волны атомом может быть двух типов: спонтанным и вынужденным. При спонтанном излучении атом переходит с верхнего энергетического уровня на нижний самопроизвольно, без внешних воздействий на атом. Спонтанное излучение атома обусловлено только неустойчивостью его верхнего (возбужденного) состояния, вследствие которой атом рано или поздно освобождается от энергии возбуждения путем излучения фотона. Различные атомы излучают спонтанно, т.е. независимо друг от друга, и генерируют фотоны, которые распространяются в различных направлениях, имеют различные фазы и направления поляризации. Следовательно, спонтанное излучение является некогерентным.

Излучение может возникать также и в том случае, если на возбужденный атом действует электромагнитная волна с частотой ν, удовлетворяющей соотношению hν=Em- En, где Em, и En -энергии квантовых состояний атома (частота ν при этом называется резонансной). Возникающее при этом излучение является вынужденным. В каждом акте вынужденного излучения участвуют два фотона. Один из них, распространяясь от внешнего источника (внешним источником для рассматриваемого атома может являться и соседний атом), воздействует на атом, в результате чего испускается фотон. Оба фотона имеют одинаковое направление распространения и поляризации, а также одинаковые частоты и фазы. То есть вынужденное излучение всегда когерентно с вынуждающим.

Атомы не только испускают, но и поглощают фотоны с резонансными частотами. При поглощении фотона атомы возбуждаются. Поглощение фотона всегда является вынужденным процессом, происходящим под действием внешней электромагнит­ной волны.

При поглощении фотонов с энергиями

hv^E_g возможны прямые переходы электронов через запрещенную зону

(здесь h - постоянная Планка, h — 6.63-10 ⁸⁴ Дж-е: v — частота излучения; E_g- ширина запрещенной зоны; полупроводниковые материалы солнечных элементов имеют эВ). Переходы, в

которых одновременно с поглощением фотона происходит поглощение или испускание фонона, называются непрямыми. 

В случае прямых переходов через запрещенную зону полупроводники имеют резкую границу полосы поглощения и относительно большие коэффициенты ослабления излучения, в случае непрямых переходов менее резкую границу полосы поглощения и меньший коэффициент ослабления.

30.Волновая функция и её статический смысл.

Предположим, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая (х, у, z, t). Эту величину называют также волновой функцией (или -функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

                                                    (216.1)

(||²=*, * — функция, комплексно сопряженная с ). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероят­ностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент време­ни t в области с координатами х и x+dx, у и y+dy, z и z+dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом dV равна

                                                           (216.2)

Величина

(квадрат модуля -функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с коор­динатами х, у, z. Таким образом, физический смысл имеет не сама -функция, а квадрат ее модуля ||², которым задается интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

Так как ||²dV определяется как вероятность, то необходимо волновую функцию  нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

                                                                      (216.3)

где данный интеграл (216.3) вычисляется по всему бесконечному пространству, т. е. по координатам х, у, z от – до . Таким образом, условие (216.3) говорит об объективном существовании частицы в пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий. Функция , харак­теризующая вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы),однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями ₁,₂,..., _n,... то она также может находиться в состоянии , описываемом линейной комбинацией этих функций:

где С_n (n=1, 2, ...) — произвольные, вообще говоря, комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей(определяемых квад­ратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция , являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние r электрона от ядра вычисляют по формуле