1. Волны: основные характеристики и определения (поперечные и продольные; амплитуда, частота, фаза, длина и фронт волны; монохроматичные волны; бегущие и стоячие волны; гармонические волны; плоские и сферические волны; понятие луча).

Волна - это колебания, распространяющиеся в пространстве в течение времени. Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле. В вакууме механическая волна возникнуть не может. В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д. Волны, рассматриваемый параметр которых изменяется периодически вдоль оси распространения, называются продольными волнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн), то такие волны называются поперечными. В продольных волнах частицы среды колеблются в направлении распространения волны. В поперечных - в плоскостях, перпендикулярных направлению распространения волны. Продольные волны могут возбуждаться в твердых, жидких и газообразных средах. Поперечные волны могут возникать только в твердых телах.

Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярнаявеличина, размерность которой совпадает с размерностью определяемой физической величины.

Амплитуда — модуль максимального отклонения тела от положения равновесия.

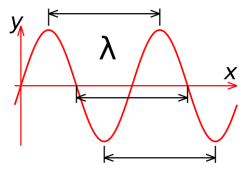
Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой λ. Измеряется в единицах расстояния (метры, сантиметры ).

Частота волны, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в герцах.

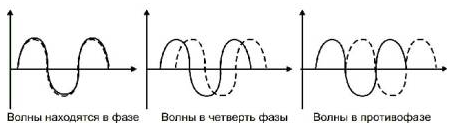
 Фаза — это позиция определенной точки волны во времени.

Для описания относительных временных свойств двух волн (или разных частей одной волны) вводится понятие фазы волны. 

Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды).

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе.

.

Фазовая скорость   этой волны даётся выражением

где   — это длина волны.

Стоячая волна является частным случаем бегущей волны с  .

То есть, две одинаковые периодические бегущие волны (в рамках справедливости принципа суперпозиции), распространяющиеся в противоположных направлениях, образуют стоячую волну.

Гармоническая волна — согласно наиболее общему определению — волна, каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания.

Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону.

Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе  )

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время  .

Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости  , т.е.

, .

– это уравнение плоской волны.

Уравнение сферической волны

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е.  ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:

, или  ,

где А равна амплитуде на расстоянии от источника равном единице.

Амплитуда колебаний   , следует из рассмотрения энергии, переносимой волной

Луч — линия, нормальная к волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причем, если волна плоская — параллельные прямые).

2. Уравнение бегущей плоской и сферической волны: волновое уравнение. Уравнение максвелла и их свойства.

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

Уравнение плоской волны

Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:   . Пусть колебание точек, лежащих в плоскости   , имеет вид (при начальной фазе   )

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время   .

Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости   , т.е.

,

– это уравнение плоской волны.

Введем волновое число

Так как   , то   . Отсюда   . Тогда уравнение плоской волны запишется так:

.

Уравнение сферической волны

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е.   ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу   . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону   . Следовательно, уравнение сферической волны:

, или  ,

где А равна амплитуде на расстоянии от источника равном единице.

Данное уравнение неприменимо для малых r, т.к. при   , амплитуда стремится к бесконечности.

Волновое уравнение

Рассмотрим плоскую волну, распространяющуюся вдоль оси x:  .

 Продифференцировав эту функцию дважды по t и дважды по x, получим

  , (1)  , (2) Сопоставив (1) и (2) и заменив   через  , получим

   - волновое уравнение, где v - скорость волны. для произвольно направленной волны.

Оператор Лапласа:  следовательно, волновое уравнение -  

3. Свойства электромагнитных волн. Шкала электромагнитных волн. Применение электромагнитных волн.

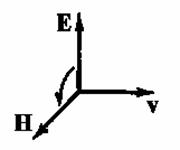
Свойства электромагнитных волн можно определить исходя из теории Максвелла. Звучит она так, переменное электрическое поле является источником магнитного поля в окружающей среде. Порождаемое поле имеет вихревой характер. То есть силовые линии его замкнуты и имеют форму окружностей.  Первым свойством электромагнитной волны является то, что она поперечна. Это значит, что векторы напряжённости электрического поля и вектор магнитной индукции колеблются в перпендикулярных плоскостях. А направление распространения волны перпендикулярно плоскости образованной векторами E и B.

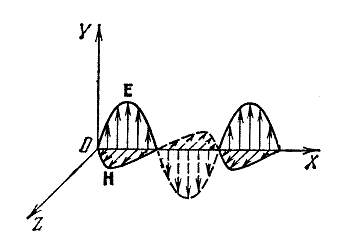
Векторы Е и H взаимно перпендикулярны, так, что вектора v, E, H

образуют правую тройку

Векторы Е и Н колеблются в одной фазе.

Модули векторов Е и Н связаны соотношением:

Шкала электромагнитных волн

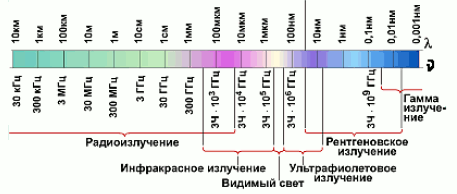
В электротехнике. Сотовая связь, беспроводный интернет, радио, телевидение, пульты управления, СВЧ-печи, радары и т.п.  Инфракрасные приборы ночного видения.  Свет от лампочек и от экранов телевизоров и мониторов.  Ультрафиолетовые детекторы фальшивых купюр.  Рентгеновские аппараты в медицине.  Гамма-телескопы на космических обсерваториях.

4.Основные законы оптики (закон прямолинейного распределения света, закон отражения, закон преломления).

Закон прямолинейного распространения света: в прозрачной однородной среде свет распространяется по прямым линиям. В связи с законом прямолинейного распространения света появилось понятие световой луч, которое имеет геометрический смысл как линия, вдоль которой распространяется свет. Реальный физический смысл имеют световые пучки конечной ширины. Световой луч можно рассматривать как ось светового пучка. Поскольку свет, как и всякое излучение, переносит энергию, то можно говорить, что световой луч указывает направление переноса энергии световым пучком. 

Закон отражения света:

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления γ есть величина, постоянная для двух данных сред:

Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: n = n2/n1.

n = V1/V2-скорости распространения волн в средах. n =C/V скорость света к скорости в среде.

5. Интерференция света: основные понятия и определения (условие возникновения интерференции, интенсивность результирующей волны, условие максимума и минимума для разности фаз и оптической разности хода, зависимость интенсивности от разности фаз).

Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Когерентные волны - это волны, испускаемые источниками, имеющими одинаковую частоту и  постоянную разность фаз.

И нтерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. При наложении когерентных волн в какой-либо точке пространства амплитуда колебаний (смещения) этой точки будет зависеть от разности расстояний от источников до рассматриваемой точки. Эта разность расстояний называется разностью хода. При наложении когерентных волн возможны два предельных случая: Условие максимума: Разность хода волн равна целому числу длин волн ( иначе четному числу длин полуволн). , где В этом случае волны в рассматриваемой точке  приходят с одинаковыми фазами и усиливают друг друга – амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде. Условие минимума: Разность хода волн равна  нечетному числу длин полуволн , где Волны приходят в рассматриваемую точку в противофазе и гасят друг друга. Амплитуда колебаний данной точки равна нулю. В результате  наложения когерентных волн (интерференции волн) образуется интерференционная картина.

 Интенсивность света пропорциональна квадрату амплитуды:   . Отсюда можно сделать вывод, что для некогерентных источников интенсивность результирующей волны всюду одинакова и равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

В случае когерентных волн    (для каждой точки пространства), так что

Последнее слагаемое в этом выражении называется интерференционным членом.

Условия максимума и минимума на разность фаз δ

6.Когерентость световых волн, длина и время когерентности. Методы получения когерентных источников.

В физике когерентностью называется согласованность нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.

– время когерентности немонохроматической волны.

      Время когерентности – время, по истечении которого разность фаз волны в некоторой, но одной и той же точке пространства  изменяется на π.

      Волна с циклической частотой ω и фазовой скоростью   распространяется за это время на расстояние

   – длина когерентности  – расстояние между точками, разность фаз в которых π.

Две когерентные световые волны можно получить в результате отражения света от двух поверхностей плоскопараллельной прозрачной пластинки ( или пленки).

7. Расчет интерференционной картины от двух когерентных источников. Кольца Ньютона. Интерференционные картины в тонких пленках, полосы равной толщины и равного наклона. Примеры применения интерференции света.

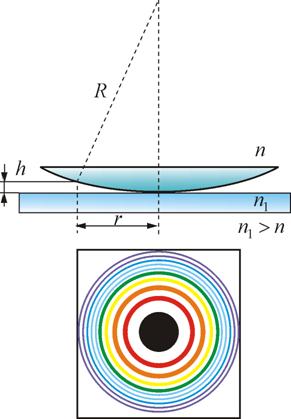
 Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны, разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания.

  Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на  лямбда/2 картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.

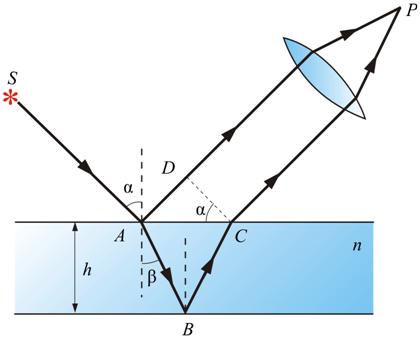
Полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом, в котором содержатся лучи разных направлений.

Светлые полосы расположены в местах, для которых   , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. 

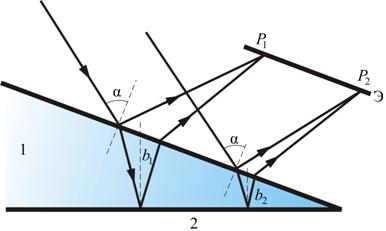1 2

Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.

Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.

      Результат интерференции в точках P(1) и P(2) экрана определяется по формуле   , подставляя в неё толщину пленки в месте падения луча. Свет обязательно должен быть параллельным α: если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.

      Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.

По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной.

Явление интерференции волн, рассеянных от некоторого объекта (или прошедших через него) с «опорной» волной, лежит в основе голографии (в т.ч. оптической, акустической или СВЧ-голографии).

Интерференционные волны от отдельных «элементарных» излучателей используются при создании сложных излучающих систем (антенн) для электромагнитных и акустических волн.

Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров.