Зависимость ΔrS от температуры:

в области ( 298 ÷Т) нет фазовых переходов: ∆_rS⁰_T = ∆_rS⁰₂₉₈ + 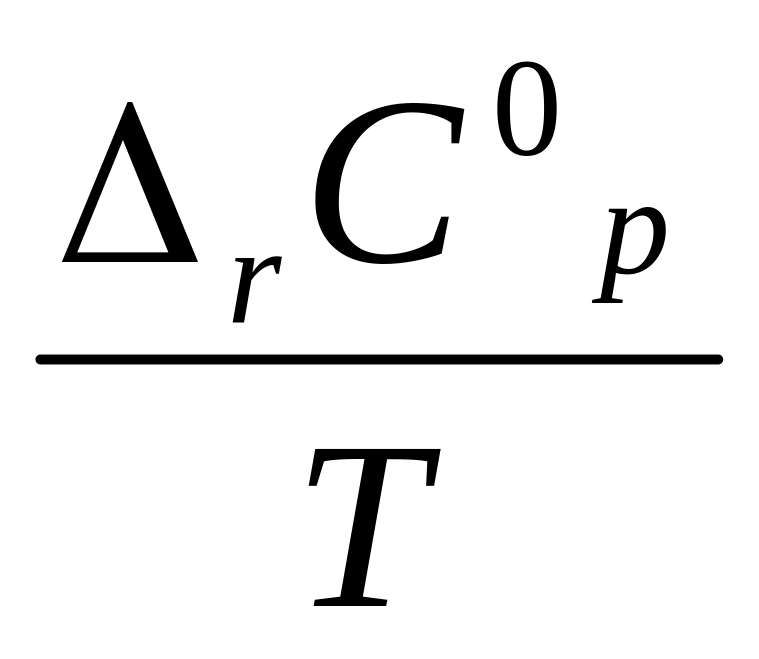dT

1 приближение: С_р  (Т) (С_р,i = соnst), тогда ∆_rС⁰_р= соnst и ∆_rS⁰_T = ∆_rS⁰₂₉₈ + ∆_rС⁰_р ln

2 приближение: при Т ~ 298 К ∆_rС⁰_р,i = 0 и ∆_rS⁰_T = ∆_rS⁰₂₉₈

3 - в области (298 ÷ Т) К есть фазовый переход. Для приближенных расчетов:

∆_rS⁰_Т = ∆_rS⁰₂₉₈ + ∆_rС⁰_р(1)( lnТ_фп - ln298) +∆_rS⁰_фп + ∆_rС ⁰_р(2)( lnТ - lnТ_фп)

Зависимость S реакции от Р особенно заметна в случае газовых реакций: ∆S_i =S^р_i – S⁰_i = - R ln(p/p⁰) изменение энтропии 1 моля газа при увеличении давления от 1 атм до р: ∆S_i = - R ln _i

Задача 11

Определите ∆_rH⁰₂₉₈, ∆_rH⁰₁₀₀₀, ∆_rS⁰₂₉₈ и ∆_rS⁰₁₀₀₀ реакции С(к) + СО₂(г) = 2СО(г), считая постоянными теплоемкости реагентов в данном температурном интервале.

Решение. ∆_rН⁰_Т = ∆_rН⁰₂₉₈ + ∆_rС⁰_р(Т - 298) ∆_rS⁰_T = ∆_rS⁰₂₉₈ + ∆_rС⁰_р ln

Табличные данные:

Вещество	ΔfН0298,кДж/моль	S0298,Дж/(моль.K)	С0р298 ,Дж/моль.К
С(графит)	0,0	5,74	8,54
СО2 (г)	-393,5	213,68	37,41
СО (г)	-110,5	197,54	29,14

По следствию из закона Гесса Δ_rН⁰₂₉₈ =∑ν_iΔ_fН_i⁰ _{продуктов} -∑ν_jΔ_fН_j ⁰_{исх веществ} =Δ_fН⁰_{298 СОг} -Δ_fН⁰_{298 Ск} -Δ_fН⁰_{298 СО2г} = 2(-110,5) – 0 – (-393,5) = 172,5 кДж > 0 - реакция эндотермическая

Т.к. С_р – функция состояния, то ∆_rС⁰_р = ∑ν_iС_{р i}⁰ _{продуктов} - ∑ν_jС_{р j} ⁰_{исх веществ} = 2С⁰_р298СОг–С⁰_р298Ск–С⁰_р298СО2г= 2^.(29,14)–8,54–37,41 =12,33 Дж/К.

∆_rН⁰₁₀₀₀ =172,5 + 12,33^.10^-3.(1000 - 298) = 181,16 кДж.

│(∆_rН⁰₂₉₈ - Δ_rН⁰₁₀₀₀)│100% /│Δ_rН⁰₂₉₈│ = │(172,5 - 181,16)│100% /172,5 = 5%.

Так как S – функции состояния, то Δ_rS⁰₂₉₈ =∑ν_iS⁰_{298,i прод.} - ∑ν_jS⁰_{298,j исх веществ} =2S⁰_298,СОг - S⁰_298,Ск - S⁰_298,СО2г = 2(197,54)–5,74–213,68=175,66 Дж/K>0 – неупорядоченность системы повышается т.к. реакция протекает с увеличением числа молей газов (Δn_газ = 2-1=1>0).

∆_rS⁰₁₀₀₀ =∆_rS⁰₂₉₈ + ∆_rС⁰_рln =175,66+12,33ln(1000/298)=175,66+14,93=190,59 Дж/К. При T = 702К

│(∆_rS⁰₂₉₈ - Δ_rS⁰₁₀₀₀) │100% /│Δ_rS⁰₂₉₈│ = │ (175,66 - 190,59 │100% /175,66  8,5%.

При изменении температуры на 702 К увеличение теплового эффекта составляет 5%, а энтропии – 8,5%.

Направление химических процессов. Энергия Гиббса. Энергия Гельмгольца Направление процесса определяется соотношением энтальпийного ∆rН (стремление системы к упорядоченности) и энтропийного Т∙∆rS (стремление системы к хаотичности) факторов реакции. Функцией состояния системы, учитывающей совместное влияние ∆rН и Т∙∆rS на самопроизвольное протекание реакции, является свободная энергия: - при P, Т = const это энергия Гиббса или изобарно-изотермический потенциал ∆rGТ=∆rНТ - Т∙∆rSТ - при V, Т = const это энергия Гельмгольца или изохорно-изотермический потенциал ∆rFТ=∆rUТ - Т∙∆rSТ Критерий термодинамической возможности самопроизвольного протекания реакции в прямом направлении: в изобарно-изотермических условиях: ∆rGТ < 0 в изохорно-изотермических условиях: ∆rFТ < 0 Соотношение между ∆rGТ и ∆rFТ: ∆rGТ - ∆rFТ = ∆n·RT Aпол = - G «свободная энергия», та часть теплового эффекта, которую можно превратить в работу. Т ΔS «связанная энергия», та часть теплового эффекта, которая рассеивается в окружающую среду rG < 0 Самопроизвольный процесс - реакция в прямом направлении rG > 0 Реакция в обратном направлении rG = 0 Реакция в равновесном состоянии
	знак					Принципиальная возможность и условия протекания прямой реакции
	∆rН		∆rS		rG
1	-	+		-			Возможна при любой температуре
2	+	-		+			Невозможна. Возможна в обратном направлении
3	-	-		-			Возможна при низких температурах 298 < Т< Тр
4	+	+		-			Возможна при высоких температурах Тр< Т< Тсущ

_rG рассчитывают двумя способами:

• 1 способ При Т=298К Δ_rG⁰₂₉₈ = ∑ν_iΔfG⁰_{298,i продуктов} - ∑ν_jΔfG⁰_{298,j исх веществ}

_Энергия Гиббса образования вещества ∆_fG – энергия Гиббса реакции образования 1 моль сложного вещества из простых веществ, устойчивых в данных условиях

∆_fG⁰- стандартная энергия Гиббса образования вещества (вещества находятся в стандартном состоянии) ∆_fG⁰_298, - табулирована кДж/моль ∆_fG⁰₂₉₈ (простых веществ)= 0

• 2 способ Δ_rG_T = ∆_rH_T - T∆_rS_T (зависимости ∆_rH и ∆_rS от Т – см. выше)

Δ_rG⁰₂₉₈ = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈

Когда ∆_rС⁰_р,i = 0: Δ_rG⁰_Т = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈

Задача 12

Рассчитать ∆_rH⁰₂₉₈ , ∆_rS⁰₂₉₈ , ∆_rG⁰₂₉₈ (двумя способами) реакции С(к) + СО₂(г) = 2СО(г) и сделать вывод о возможности самопроизвольного протекания реакции при стандартных состояниях веществ и 298 К.

Решение: Табличные данные:

Вещество	ΔfН0298, кДж/моль	S0298, кДж/(моль.K)	∆fG0298, кДж/моль
С(графит)	0,0	5,74	0,0
СО2 (г)	-393,5	213,68	-394,4
СО (г)	-110,5	197,54	-137,14

Следствие из закона Гесса: энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов ν

Так, для веществ в стандартных состояниях при Т=298 К (табличная Т)

Δ_rН⁰₂₉₈ =∑ν_iΔ_fН_i⁰ _{298 продуктов} -∑ν_jΔ_fН_j ⁰ _{298 исх веществ}=2Δ_fН⁰₂₉₈ СО(г)- Δ_fН⁰₂₉₈ С(к) - Δ_fН⁰₂₉₈ СО₂(г)=2(-110,5)–0 –(-393,5) = 172,5 кДж. Δ_rН⁰₂₉₈ >0 - реакция эндотермическая

S и G – функции состояния и для них:

Δ_rS⁰₂₉₈ =∑ν_iS⁰_{298,i продуктов}-∑ν_jS⁰_{298,j исх веществ}=2S⁰₂₉₈СО(г)-S⁰₂₉₈ С(к)- S⁰₂₉₈ СО₂(г)= 2(197,54)–5,74–213,68=175,66 Дж/K Δ_rS⁰₂₉₈ >0 - реакция протекает с увеличением числа молей газообразных веществ ∆ν_газ = 2 – 1 = 1>0

Δ_rG⁰₂₉₈ = ∑ν_iΔ_fG⁰_{298,i продуктов} - ∑ν_jΔ_fG⁰_{298,j исх веществ} = 2Δ_f G⁰₂₉₈ СО(г) - Δ_f G⁰₂₉₈ С(к) - Δ_f G⁰₂₉₈ СО₂(г) =2(-137,14) – 0 – (-394,4) = 120.09 кДж

2 способ: при Т=298 К ∆_rG⁰₂₉₈ = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈ = 172,5 – 298^.175,66^.10^-3 = 120,15 кДж

Значения ∆_rG⁰₂₉₈, рассчитанные двумя способами практически совпадают.

Критерий термодинамической возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях – уменьшение энергии Гиббса системы: ∆_rG_Т < 0

Т.к. ∆_rG⁰₂₉₈ > 0 – самопроизвольное протекание реакции при стандартных состояниях всех участников и Т=298 К в прямом направлении невозможно, реакция будет протекать в обратном направлении.

Задача 13

Определить температурную область самопроизвольного протекания реакции С(к)+ СО₂(г) = 2СО(г) при стандартных состояниях компонентов (Δ_rН⁰₂₉₈ =172,5 кДж, ∆_r S⁰₂₉₈ =^.175,66 Дж/К)

Решение

Вещество	Интервал температур, .К
С(графит)	(298 – 2300) К
СО2 (г)	(298 – 2500) К
СО (г)	(298 – 2500) К

Т_сущ. = 2300 К (для наименее устойчивого вещества - графита)

∆_rG_Т=∆_rН_Т - Т∙∆_rS_Т - энергия Гиббса или изобарно-изотермический потенциал, это функция состояния системы, учитывающая совместное влияние энтальпийного (∆_rН) и энтропийного (Т∙∆_rS) на самопроизвольное протекание реакции при P, Т = const (свободная энергия).

Реакция протекает самопроизвольно при стандартных состояниях компонентов, если ∆_rG⁰_Т = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈ < 0. С учетом приближения 2: ∆_rH⁰_Т = ∆_rH⁰₂₉₈ и ∆_rS⁰_Т = ∆_rS⁰₂₉₈ (энтальпия и энтропия реакции не зависят от температуры), график зависимости ∆_rG⁰_Т (Т) линейный.

При температуре равновесия Т_р = ∆_rH⁰₂₉₈ /∆_rS⁰₂₉₈ = 172,5/175,66^.10^-3 = 928 K – равновероятно протекание как прямой, так и обратной реакции т.к. при этой температуре ∆_rG⁰_Т = 0.

Энтальпийный фактор (стремление системы к упорядоченности) Δ_rН⁰₂₉₈ =172,5 кДж >0 не способствует протеканию реакции при низких температурах, а энтропийный фактор (стремление системы к хаотичности) Т∙∆_r S⁰₂₉₈ = Т^.175,66 Дж >0 определяет отрицательный знак энергии Гиббса при высоких температурах. Сл. самопроизвольное протекание процесса при стандартных состояниях возможно при Т>Т_р.

Область температур, в которой возможно самопроизвольное протекание реакции при стандартных состояниях веществ (∆_rG⁰_Т<0):

∆_rG⁰_Т , кДж

Т _р= 982 К < Т < 2300К = Т_сущ..

∆_rG⁰₂₉₈ = 120,09

∆_rG⁰_Т = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈

Т_р Т_сущ

298 982 2300 Т, К

∆_rG⁰_Т<0

Зависимость Δ_rG_T от давления - изотерма Вант Гоффа:

Для реакции: aA_г + bB_г + dD_к = eE_г + fF_г Δ_rG_Т = ∆_rG⁰_Т + RTln

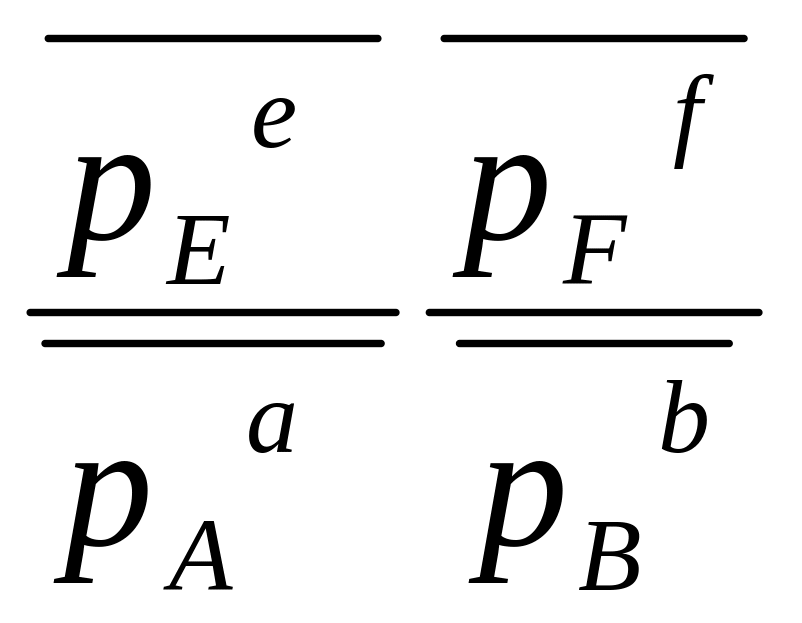
где – относительные парциальные давления газообразных веществ.

Для реакции: aA(р)+bB(р)+dD(к) = eE(р)+fF(р) протекающей в идеальном растворе (∆V = 0) ∆_rGº_T=∆_rFº_T= - RTln (c^e_{E равн} c^f_{F равн} / c^a_{A равн} c^b_{B равн})

Задача 14

При каком соотношении парциальных давлений газообразных компонентов реакции С(к)+СО₂(г)=2СО(г) возможно ее протекание в прямом направлении при 298К (∆_rG⁰₂₉₈ = 120,15 кДж)?

Решение

Возможность самопроизвольного протекания реакции определяется ∆_rG₂₉₈< 0

По уравнению изотермы Вант-Гоффа: Δ_rG₂₉₈=∆_rG⁰₂₉₈+RTln < 0.

Пусть = х, тогда 120,15+8,31^.10^-3.298 lnх<0, отсюда lnх<-48,5  х= <10^-21 или

Задача 15

Определите, изменится ли направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10 Па для реакции С(к)+СО₂(г)=2СО(г) при Т = 1000 К (Δ_rН⁰₂₉₈ =172,5 кДж, ∆_r S⁰₂₉₈ =^.175,66 Дж/К)

Решение

Зависимость Δ_rG_T от давления выражается изотермой Вант Гоффа (С(к)- вещество в кристаллическом состоянии не входит в ):

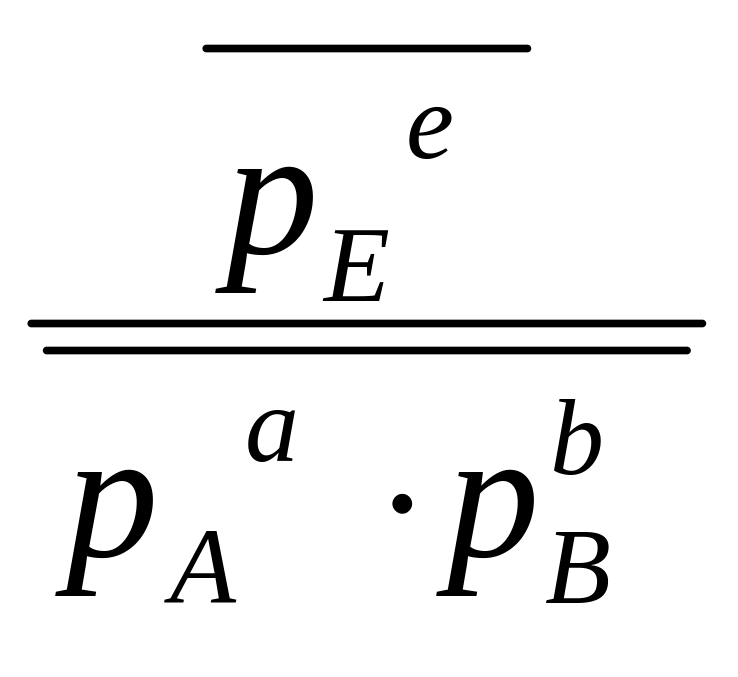Δ_rG_Т = ∆_rG⁰_Т + RTln при Т=1000 К Δ_rG₁₀₀₀ = ∆_rG⁰₁₀₀₀ + RTln

Энергия Гиббса реакции при стандартных состояниях веществ, т. е. относительных парциальных давлениях СО₂ и СО равных 1: Δ_rG⁰_Т = ∆_rH⁰₂₉₈ - T∆_rS⁰₂₉₈ (считая ∆_rС⁰_р = 0, т.е. ∆_rH⁰_Т = ∆_rH⁰₂₉₈ и ∆_rS⁰_Т = ∆_rS⁰₂₉₈ - энтальпия и энтропия реакции не зависят от температуры)

при Т=1000К Δ_rG⁰₁₀₀₀ = 172,5- 1000∙175,66^.10^-3 = -3,16 кДж ˂ 0 – возможно самопроизвольное протекание реакции при стандартных состояниях и Т=1000К

Для заданных начальных состояниях веществ, отличных от стандартных Δ_rG₁₀₀₀ =-3,16+8,31^. 10 ^{-3 .} 1000 ln(1/10^-1) =-3,16+19,11=15,95 кДж ˃ 0 - направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10 Па изменилось и самопроизвольное протекание процесса в прямом направлении при заданных начальных условиях и Т=1000 К невозможно.

∆_rG⁰₁₀₀₀ ˂ 0 ˂ Δ_rG₁₀₀₀