1.Инженерная графика - наука создания проекционных изображений.Инженерная графика - это дисциплина, которая состоит из двух частей: начертательной геометрии и технического черчения.
2. Центральное проецирование
Для перехода от пространственного представления о предмете к его плоскому изображению используется метод проекций. Для того чтобы трехмерный объект, находящийся в трехмерном пространстве, "перенести" на плоскость, т. е. получить его изображение, необходимо его спроецировать. Для этого, из выбранной определённым образом точки пространства, которая называется центром проекции, необходимо провести прямые линии (лучи) через каждую точку изображаемого объекта. Эти прямые называются проецирующими прямыми. Та плоскость, на которой мы получили изображение предмета называется плоскостью проекции, а изображение предмета, которое мы получим на этой плоскости называется его проекцией.
Параллельное проецирование
Параллельное проецирование можно рассматривать как частный случай центрального проецирования. Если центр проекций при центральном аппарате проецирования перенести в бесконечность, то проецирующие лучи можно считать параллельными. Отсюда аппарат параллельного проецированиясостоит из плоскости проекций П и направления Р. При центральном проецировании проецирующие лучи выходят из одной точки, а при параллельном проецировании - параллельны между собой.
3. Некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.
4. В многомерном пространстве любое изображение объекта на плоскости можно получить с помощью проецирования. Однако не стоит судить о геометрической форме тела либо о форме простейших образов в геометрии на основе одной проекции точки. Наиболее полную информацию об изображении геометрического тела дает несколько проекций точек. Для чего используют проекции точек тела минимум в двух плоскостях.
Например, необходимо построить проекцию точки А. Для этого расположите две плоскости перпендикулярно друг другу. Одну -горизонтально, называя ее горизонтальной плоскостью и обозначая все проекции элементов с индексом 1. Вторую - вертикально. Назовите ее, соответственно, фронтальной плоскостью, а проекциям элементов присвойте индекс 2. Обе эти плоскости считайте бесконечными и непрозрачными. Линией их пересечений становится ось координат ОХ.
Затем примите как факт, что пространство между плоскостями проекции условно делится на четверти. Вы находитесь в первой четверти и видите только те линии и точки, которые находятся в этой области двугранного угла.
Суть процесса проецирования состоит в проведении луча через заданную точку, пока луч не встретится с плоскостью проекций. Данный метод получил название метода ортогонального проецирования. Согласно нему, опустите из точки А перпендикуляр на горизонтальную и фронтальную плоскость. Основанием этого перпендикуляра как раз и будет горизонтальная проекция точки А1 либо фронтальная проекция точки А2. Таким образом, вы получите положение этой точки в пространстве заданных плоскостей проекций.
5. Определение натуральной величины отрезка прямой линии
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Натуральные размеры отрезков линий и фигур получаются на той плоскости проекций, параллельно которой они расположены. Следовательно, чтобы определить натуральную величину отрезка линии или фигуры, необходимо, чтобы плоскость проекции была параллельна изображаемому элементу. Для этого применяют способ вращения и способ перемены плоскостей проекций.
определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям.
6. Взаимное положение прямых линий.
1. Определение параллельных прямых.
Прямые линии называются пересекающимися, если они имеют только одну общую точку.
Так, например, прямые АВ и СDимеют только одну общую точку О; эти прямые пересекающиеся. Прямые ЕF и МN также пересекающиеся (черт. 182, 183).
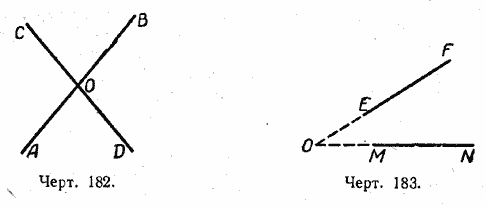
Две прямые, лежащие в одной плоскости и не имеющие ни одной общей точки, называются параллельными (черт. 184).
Параллельность прямых обозначается знаком || . Если прямые АВ и СD параллельны, то пишут: АВ || СD.
Представление о параллельных прямых дают нам линии в разлинованных ученических тетрадях (в линейку и в клетку), противоположные края листа бумаги, тетради, стола, переплёты оконных рам.
2. Параллельные отрезки.
Если два отрезка расположены на параллельных прямых линиях, то эти отрезки также называются параллельными. На чертеже 185 АВ || СD, отрезки МN и ЕF, расположенные на них, будут параллельными.
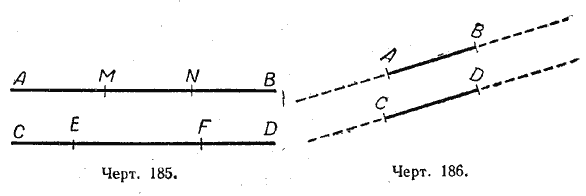
Точнo так же называются параллельными два отрезка, если при неограниченном продолжении их образуются параллельные прямые (черт. 186).
3. Свойство двух перпендикуляров к одной и той же прямой.
Теорема. Если две прямые АВ и СD перпендикулярны к одной и той же прямой МN (черт. 187), то они параллельны.
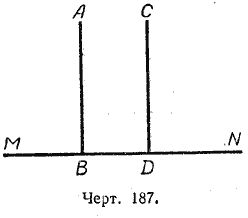
В самом деле, если бы АВ и СD были не параллельны, т. е. имели бы общую точку, например точку О, то тогда из одной и той же точки О на прямую МN было бы опущено два перпендикуляра, а этого быть не может (§ 26).
7.а) Плоскость общего положения - плоскость не перпендикулярная ни к одной из плоскостей проекций.
Плоскость частного положения - плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью.
ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ |
|
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный П1; - фронтальный П2; - профильный П3).
2. Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (П), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости является прямая линия, совпадающая со следом П2
2.3. Плоскость, перпендикулярная профильной плоскости ( П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость