
- •17. Каждое из данных множеств может быть задано неоднозначно: несколько формул могут выражать одно и тоже множество.
- •Глава 2
- •Глава 3
- •Глава 4.
- •Глава 5
- •Глава 6
- •Глава 8
- •Литература
- •Приложения
- •Тема1. Множества и операции над ними
- •Тема 2. Числовые множества. Проценты
- •Тема 3. Элементы математической логики
- •Тема 4. Предикаты
- •Тема 5. Элементы комбинаторики и теории вероятностей
Глава1
2. а)
Элементы данного множества – натуральные
числа, меньшие 8, т. е. имеем множество
{x | х
N, x<8}; б)
Элементы данного множества образуют
первые 6 членов арифметической прогрессии,
у которой первый член и разность равны
4, иначе говоря, речь идет о множестве
{![]() };
в)
};
в)
![]() ;
г)
{x | x
Q, x2
= 2};
д)
{x | x = (1)n(xn+3),
где x1=
5,
n
5}; е)
{x | x – простое, x
19}.
;
г)
{x | x
Q, x2
= 2};
д)
{x | x = (1)n(xn+3),
где x1=
5,
n
5}; е)
{x | x – простое, x
19}.
6. a) По степени общественной опасности во множестве А всех правонарушений выделяются два подмножества: В – множество преступлений и С – множество проступков; А = В С . В свою очередь, С = С1 С2 С3 С4 , где С1 – множество гражданско-правовых, С2 – множество конституциональных, С3 – множество административных, С4 – множество дисциплинарных проступков.
b) по сферам общественной жизни А = D E F T, где
D – множество правонарушений в экономике, E – множество правонарушений в политике, F – множество правонарушений в социально-бытовой сфере, Т– множество правонарушений в культурной (общественной) сфере.
7. а) АВ = (1, 8), АВ = ; б) АВ = (–3, 8), AB = [5, 6].
8. АВ= {1, 2, 3, 4, 5, 6, 8, 9}, AB = {4, 9}, А\В= {1, 2, 6}, В\А = {3, 5, 8}.
9. 1) ABCD = {3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, 2) ABCD = {3, 4}, 3) (А В) ( С D) = {2, 3, 4, 5, 6, 7}, 4) (A B) (C D) ={0, 1, 2, 3, 4, 5, 6}.
10. Решение.
А – множество отцов (отец и дед мальчика), |А| = 2,
В – множество сыновей (мальчик и его отец), |В| = 2,
С – состоит из тех и только тех элементов, которые принадлежат множеству А или множеству В. С = А В, |С| = 3, так как отец мальчика принадлежит множествам А и В.
11. 1) АВ = N, 2) АВ = , 3) А \ В = A.
12. АВ = {х | х N, x делится на 6}, ВС = {х | х N, x делится на 15},
АВС = {х | х N, x делится на 30}.
13. г) д)
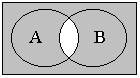
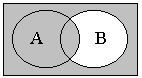
е) Этот пример аналогичен предыдущему;
ж)
Объединение множеств
![]() (),
(),
![]() ()
(см. п. в)
) будет таким:
()
(см. п. в)
) будет таким:

з)
Воспользуемся законом де Моргана:
![]() =
=
![]() .
Значит, ответ будет такой же, как и в
задаче в).
.
Значит, ответ будет такой же, как и в
задаче в).
и) Изобразим множества А \ В (1) и В \ А (2):
(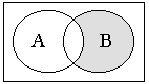
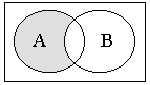 1)
(2)
1)
(2)
Их объединением будет множество, представленное ниже:

к
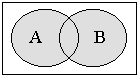 )
Покажем объединение и пересечение
множеств А и В:
)
Покажем объединение и пересечение
множеств А и В:
Их разностью будет множество:
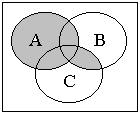
14. а) Решение.
Сначала изобразим множества, находящиеся в скобках, а затем требуемое множество.
а
 )
)
б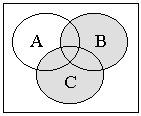
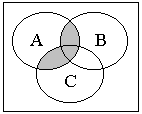 )
)
в)


г)
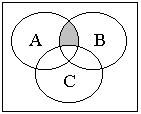
д
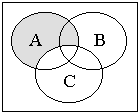
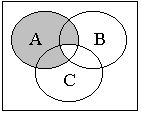 )
)
е)
17. Каждое из данных множеств может быть задано неоднозначно: несколько формул могут выражать одно и тоже множество.
1)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
и т. д.
,
и т. д.
2)
((А \ B)
\ C)
A
B
C;
(А
![]() )
A
B
C;
и т. д.
)
A
B
C;
и т. д.
3)
Возможные ответы: (А
В
С)![]() ;
;
((А \ B) \ C) ((С \ B) \ А) ((В \ А) \ C) .
4) ((С В) \ А)\ (В С)) А В С.
5) ((А С) \ (A В С)) ( В \ ((А В) (В С));
((А С) \ В) (В \ (А С)).
6) Элементы этого множества принадлежат ровно двум из множеств
А, В, С. Возможны варианты:
(А (В \ C)) (А (C \ B)) (B (C \ A));
((А В) \ C) ((А C) \ B)) ((B C) \ A));
((А В) (А C) (B C)) \ (A B C).
18. 1) А (А В) = (А ) (А В) = А (В ) = А = А.
2)
(P
Q)
![]() (
(![]()
P)
= Р.
P)
= Р.
3) (А В ) ( А В) ((В С ) =
= (А (В )) ( А В) (В (С )) =
= (А ) ( А В) (В ) = ( А В) = А В.
4)
(А
В)
((А
В)
(![]()
B))
= В.
B))
= В.
22. 1) В А; 2) А = В; 3) А В; 4) А = В;
5)![]()
![]() ;
6)
В
А, В
А; 7)
В
А; 8)
В
А.
;
6)
В
А, В
А; 7)
В
А; 8)
В
А.
25.
а)
2, б)
35, в)
50. 26. 22,
30. 27.
20, 13, 20,14.
28. 11,
1, 3. 29.
3,
3.
30. 10.
31. 30.
32.
10. 33. 3,
9. 39. 26.
40. 435.
41.
1. 42.
15. 44. 50%,
10%. 45.
18, 12, 5. 49.
20.
50. 25;20. 51.
147.
52. 60, 36.
53. 20. 54.
36.
55. 9, 20.
56. 29.
57. 37.
58. 900.
59.
4536; 60.
9!. 61.
42. 62.
13800. 63.
81. 64.
54. 65.
![]() .
66. 992.
67.
9, 9, 8. 68.
1024, 992, 4032. 69.768.
70.
294. 72. 3m.
73. 336.
74. 55440.
75.
2(5!)2.
77. 1) 151200,
2)
.
66. 992.
67.
9, 9, 8. 68.
1024, 992, 4032. 69.768.
70.
294. 72. 3m.
73. 336.
74. 55440.
75.
2(5!)2.
77. 1) 151200,
2)
![]() ;
3)
;
3)![]() .
78. 1) 1560,
2)
96. 79.
.
78. 1) 1560,
2)
96. 79.
![]() =3 185.
80.
=3 185.
80.
![]() .
81.
.
81.
![]() .
82. 37512.
83. а)4, б)36.
84.
.
82. 37512.
83. а)4, б)36.
84.![]() .
85. 1)
60, 2) 24.
86.
.
85. 1)
60, 2) 24.
86.
![]() .
87.
.
87.![]() .
88.
.
88.
![]() 89.
7054320. 90.
1500. 91.
28800.
92.
89.
7054320. 90.
1500. 91.
28800.
92.![]() .
93.
99!.
94.
4080.
96.
303600. 97.
78.
98.
10.
99.
47.
118.
.
93.
99!.
94.
4080.
96.
303600. 97.
78.
98.
10.
99.
47.
118.
![]() .
119.
10.
120.
.
119.
10.
120.
![]() .
121.
.
121.
![]() .
.
122.
а)
![]() ;
б)
1; в)
;
б)
1; в)
![]() .
.
123.
а)
0,(428571); b)
0,035; c)
0,0304; d)
0,(571428); e)
![]() .
.
124.
Q;
R;
![]() ;
[-1; 6];
;
[-1; 6];
![]() ;
;
![]() .
.
125.
![]() ;
7; -1 .
;
7; -1 .
126. 1) (0; 8]; 2) (-4; 11); 3) (0; 9); 4) (-4; 2)(0; 11); 5) .
127. AB={15t+2tN}, AC={–6t+5tN},
ABC={30t+17tN}, ABC={15t+2tN}{2n+1nN}.
128.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
129.
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)7;
5)4;
6)3.
;
4)7;
5)4;
6)3.
139. 13 = 11012 = 167 = 158; 50 = 1100102 = 1017 = 628.
140.
101101102
= 182;
![]() .
.
141.
4417
= 225;
![]() .
.
143.
1)![]() ;
3)
4920412
.
;
3)
4920412
.
145. А и В, D и Е.
146. Все.
148. а), б) – континуум.
150. Используйте метод, которым решена предыдущая задача.
153. х = (b а)t + а.
155. а) Каждой точке окружности поставим в соответствие численное значение угла, образованного радиус-вектором этой точки с некоторым фиксированным радиусом.
б) Искомая биекция является композицией трех отображений: 1) отображения, построенного в задаче а), 2) линейного отображения промежутка [0, 2) на промежуток [0, 1) и 3) отображения промежутка [0, 1) на отрезок [0, 1], которое строится также, как отображение задачи 4.11.
158.
53,2%. 159.
32,8.
160.
232.
161.
14474901. 162.
37186. 168.
81%. 171.
30. 173.
![]() %.
174.
900%. 175.
90. 176.
300. 177.
230 млн. руб.. 178.
5084,21р. 179.
3%. 182.
874,18. 183.
S(t)=
S(0)
%.
174.
900%. 175.
90. 176.
300. 177.
230 млн. руб.. 178.
5084,21р. 179.
3%. 182.
874,18. 183.
S(t)=
S(0)![]() ,
t=1,
2, 3,…. 184.
4. 186.
25%. 188.
21%. 189.
а)
увеличится на 50 %; б)
уменьшится на 4 %. 190.
увеличится на 38,24 %. 191.
уменьшится на 1 %. 192.
7%. 193.
10%. 194.
10%. 195.
25%. 196.
25%. 197.
9800 руб.. 198.
576. 199.
40 л. 200.
38,5%. 201.
49,6%. 203.
50%. 204.
25%. 5205.
30%. 206.
40%. 207.
25%. 208.
20%. 209.
25%. 212.
8,75%. 213.
17 100, 11 400 руб. 214.
2 млн 400 тыс. руб. и 3 млн. 600 тыс. руб.
,
t=1,
2, 3,…. 184.
4. 186.
25%. 188.
21%. 189.
а)
увеличится на 50 %; б)
уменьшится на 4 %. 190.
увеличится на 38,24 %. 191.
уменьшится на 1 %. 192.
7%. 193.
10%. 194.
10%. 195.
25%. 196.
25%. 197.
9800 руб.. 198.
576. 199.
40 л. 200.
38,5%. 201.
49,6%. 203.
50%. 204.
25%. 5205.
30%. 206.
40%. 207.
25%. 208.
20%. 209.
25%. 212.
8,75%. 213.
17 100, 11 400 руб. 214.
2 млн 400 тыс. руб. и 3 млн. 600 тыс. руб.
