8.,1. Задача линейного программирования
Задачей линейного программирования называют задачу отыскания оптимума (максимума или минимума) заданной линейной функции от нескольких переменных, если ее аргументы удовлетворяют системе линейных уравнений или неравенств. Математическая формулировка этой задачи выглядит следующим образом.
Найти наибольшее (наименьшее) значение
функции
,
аргументы которой удовлетворяют
системе ограничений:
Здесь, коэффициенты
,
,
– заданные числа, причем можно считать,
что все числа
.
Кроме того, следует иметь в виду, что
система ограничений помимо уравнений
может содержать и неравенства и что
переменные, как правило, удовлетворяют
условиям
,
которые называются условиями
неотрицательности.
Решение
системы
ограничений, при котором функция цели
достигает своего наибольшего (наименьшего)
значения, называется оптимальным.
Задача линейного программирования является математической моделью многих практических задач экономического содержания. Некоторые из низ указаны на ниже приведенной схеме.
Рассмотрим отдельные из них.
1. Задача об оптимальном использовании ресурсов
Пусть предприятие выпускает
различных изделий
.
Для их производства требуется
различных видов ресурсов (разных видов
сырья, вспомогательных материалов,
людских ресурсов и т.д.). Эти ресурсы
ограничены и составляют в планируемый
период соответственно
условных единиц.
Известны также технологические
коэффициенты
,
которые показывают, сколько единиц
-го
ресурса требуется для производства
одной единицы изделия
.
Пусть прибыль от реализации одной единицы изделия равна денежных единиц. В планируемый период все показатели , и предполагаются постоянными.
Составить такой план выпуска продукции, при котором прибыль предприятия от ее реализации была бы наибольшей.
Решение. Прежде чем составить математическую модель этой задачи, сведем все данные в таблицу:
Виды ресурсов |
Запасы ресурсов |
Технологические коэффициенты |
|||||
|
|
… |
|
… |
|
||
1 |
|
|
|
… |
|
… |
|
2 |
|
|
|
… |
|
… |
|
… |
… |
… |
|
… |
… |
… |
… |
i |
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
m |
|
|
|
… |
|
… |
|
Прибыль |
|
|
… |
|
… |
|
|
Планируемый выпуск |
|
|
… |
|
… |
|
|
Составим ограничение на ресурсы. Использование -го ресурса на изготовление всех видов изделий не должно превышать запас этого ресурса, поэтому получаем систему
Из условия задачи ясно, что
,
,
…
.
Прибыль от реализации продукции
выражается функцией
.
Требуется найти такие неотрицательные
значения переменных
…,
,
при которых функция
достигает наибольшего значения.
Заметим, что если использовать все имеющиеся запасы ресурсов, то неравенства в системе ограничений обращаются в равенства.
1. Для изготовления изделий №1 и №2 склад может отпустить металла не более 80 кг, причем на одно изделие №1 расходуется 2 кг, а на изделие №2 – 1кг металла. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий №1 требуется изготовить не более 30 шт., а изделий №2 – не более 40 шт., причем одно изделие №1 стоит 5 руб., а №2 –3 руб.
Решение. Составим
математическую модель задачи. В качестве
переменных здесь выступает план выпуска
изделий. Пусть спланировано выпустить
изделий №1
шт., а изделий №2 –
шт. По условию задачи
,
.
На изготовление всех изделий металла
потребуется
кг . По условию запасы металла составляют
80 кг, поэтому должно выполняться условие
.
Прибыль от реализации всех изготовленных
изделий составит
рублей. Итак, получена математическая
модель этой конкретной задачи.
Найти такие решения системы
при которых функция
принимает наибольшее значение. Для
решения задачи используем графический
метод. Для этого на координатной плоскости
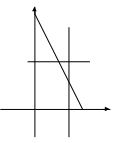
изобразим множество точек, координаты
которых удовлетворяют заданной системе
неравенств (рис. 1). Решением системы
является заштрихованный пятиугольник.
В каждой точке плоскости
функция
принимает конкретное значение
.
Множество точек, для которых
,
есть прямая линия, которая проходит
перпендикулярно вектору
.
Рассмотрим прямую
. Если эту прямую передвигать параллельно
самой себе в направлении нормального
вектора
,
то значения функции
будут возрастать.
Вершина,
в которой прямая при движении в направлении
вектора
впервые встретится с многоугольником
решений, будет точкой, в которой функция
цели принимает наименьшее значение.
Последняя общая вершина движущейся
прямой и многоугольника (точка выхода)
– точкой, в которой функция цели принимает
наибольше значение. В нашей задаче
искомой точкой будет точка (20,40). В ней
.
Таким образом, чтобы получить максимальную прибыль предприятие должно выпустить 20 изделий первого типа и 40 изделий второго типа. Прибыль при этом составит 220 рублей.
2. Производственная мощность цеха
сборки составляет120 изделий типа
и 360 изделий типа
в сутки. Технический контроль пропускает
в сутки 200 изделий того или другого типа
(безразлично). Изделия типа
вчетверо дороже изделий типа
.
Требуется спланировать выпуск готовой
продукции так, чтобы предприятию была
обеспечена максимальная прибыль от
этого цеха.
Решение. Пусть по плану
надо выпустить
изделий типа
и
изделий типа
. По условию
и
,
.
Получили систему ограничений. Пусть
цена реализации одного изделия типа
составляет
1 ден. ед. Тогда для изделия типа
она составляет 4 ден. ед. Прибыль от
реализации всех изготовленных по плану
изделий составит в итоге
ден. ед. Требуется, чтобы значение
было максимальным. Получили задачу
линейного программирования. Решите ее
графически самостоятельно. (Ответ:
).
3. Составить математическую модель следующей задачи.
Найти оптимальное распределение двух
видов механизмов, имеющихся в количествах
,
между тремя участками работ, потребности
которых соответственно равны
,
,
при следующей матрице производительности
каждого из механизмов на соответствующем
участке работы:
4. Для изготовления изделий №1 и №2 имеется 100 кг металла. На изготовление изделия №1 расходуется 2 кг, а на изделие №2 – 4 кг металла. Составить план производства, обеспечивающий наибольшую выручку от продажи изделий, если отпускная стоимость одного изделия №1 составляет 3 руб., а изделия №2 –2 руб., причем требуется изготовить изделий №1 не более 40 шт., а изделий №2 – не более 20 шт.
5. Производственная мощность завода позволяет производить за месяц 200 электродвигателей типа и 600 электродвигателей типа . Определите, сколько электродвигателей каждого типа должен производить завод для достижения максимальной прибыли, если: 1) двигатели обоих типов имеют одинаковую цену;
2) цена на двигатель типа в три раза больше цены двигателя типа ;
3) цены на двигатели типов
и
относятся как
.
6. Автомобильный завод выпускает автомобили типов и . Производственные мощности отдельных цехов или отделов приведены в следующей таблице:
Наименование цехов или участков |
Количество машин за год |
||
Типа |
Типа |
||
1 2 3 4 5 6 |
Подготовка производства автомобилей Кузовной Производство шасси Производство двигателей Сборочный Участок испытаний |
125 80 110 240 160 280 |
110 320 110 120 80 70 |
Определите наиболее рентабельную производственную программу в следующих случаях: 1) прибыли от выпуска одной машины типов и соответственно равны 200000 600000 рублей;
2) выпуск одной машины приносит прибыль в 2 раза меньшую, чем выпуск одной машины ;
3) в задаче1) производственная программа ограничена сверху условиями: машин типа не более 50, а машин типа не более 60.
7. Из города в город ежедневно отправляются пассажирские и скорые поезда. В таблице указаны наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные составы, и количество пассажиров, вмещающихся в каждый из вагонов:
Поезда |
Вагоны |
||||
багажный |
почтовый |
ж. плацк. |
куп. |
мягк. |
|
Скорый Пассажирский Число пассажиров Парк вагонов |
1 1 – 12 |
1 – – 8 |
5 8 58 81 |
6 4 40 70 |
3 1 32 26 |
Определите оптимальное число скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.
8. Решите задачу 7, если пропускная способность дороги не позволяет в день пройти более, чем 6 пассажирским поездам.