План вивчення теми.

1. Диференціальні рівняння першого порядку.

2. Диференціальні рівняння з відокремленими змінними..

3. Приклади.

Домашне завдання: конспект, індивідуальні завдання.

1. Диференціальні рівняння першого порядку.

Диференціальним рівнянням називається рівняння, що зв'язують між собою незалежну змінну х, шукану функцію у і її похідні або диференціали.

Символічно диференціальні рівняння записують так:

; ;

Порядком диференціального рівняння є найбільший порядок похідних, що входять в дане рівняння.

Диференціальним рівнянням першого порядку називається рівняння вигляду

Вирішуючи дане рівняння, якщо це можливо, відносно похідній у`, отримаємо у` = f (x;y).

Дане рівняння називається рівнянням першого порядку, дозволеним відносно похідною. Іноді ці рівняння записуються в диференціалах і мають вигляд :

P(x; у) dx + Q(x; у) dy = 0

Рішенням диференціального рівняння називається така функція, яка обертає це рівняння в тотожність.

Кожному диференціальному рівнянню відповідає нескінченна сукупність його рішень. Загальним рішенням диференціального рівняння називається таке рішення, в яке входить стільки незалежних довільних постійних, який порядок рівняння. Загальне рішення диференціального рівняння першого порядку містить одну довільну постійну.

Всяке окремо взяте рішення диференціального рівняння називається його частним рішенням. З геометричної точки зору сукупність всіх рішень диференціального рівняння є сімейство кривих, званих інтегральними кривими, а кожне часне рішення представляє окрему інтегральну криву.

Для того, щоб зі всієї сукупності рішень виділити окрему інтегральну криву, задають так звані початкові умови. Під початковими умовами для вирішення рівняння y`= f (x;y) розуміють умови, що полягають в тому, що при x = x т. е у(x)= у , де x , y- задані числа такі, що при x = x і у = y функция f (x;y) має сенс т. е існує f(x ; у ).

Завдання знаходження часного рішення диференціальне рівняння, що задовольняє заданою початковою умовою завдання Коші.

Для диференціального рівняння першого порядку завдання Коші наступне: знайти рішення у=у(х) рівняння у`= f(x:y), що задовольняє при заданих початкових даних (x ;y ) початковій умові у(x),

або у= у, де x , y- задані числа.

Геометрично, рішення, що задовольняє початковій умові у(x)= у представляє інтегральну криву, що проходить через дану крапку (x ;y ).

Диференціальні рівняння із змінними, що розділяються

Диф рівнянням називається рівняння із змінними, що розділяються, якщо має наступні вигляд : y'= f(x) f(y) (1)

Для даного рівняння завдання Коші про існування і єдиність рішення наступна : Якщо функція f(x) безперервна в інтервалі (а;b), функція f(x) і її похідна по у безперервна в інтервалі (з;d), то для будь-яких початкових даних хе (а;b), yе (з;d), у=ц(х) рівняння (1), що задовольняє початковій умові ц(x)= ц

Рівняння вигляду називається рівняння з роздільними змінними.

При рішенні рівнянь із змінними, що розділяються, виконати наступне:

1. Розділити змінні.

2. Інтегрований почленно отримане рівняння і знаходимо його загальне рішення.

3. Знайти приватне рішення, що задовольняє початковим умовам (якщо це не потрібно)

Диф рівняння типу M(x)dx + N(g)dy=0 або dy(f(y)= f(x) dx -

називають рівнянням з відокремленими змінними.

Загальне рішення має вигляд:

Приклад 1. Знайти загальне рішення рівняння xdx+ydy=0,интегрируем і отримуємо т.к ліва частина ненегативна, то і права теж ненегативна. Хай 2С= С, тоді отримаємо x+y=с .

Це рівняння сімейства концентричних кіл з центром на початку координат і радіусом С..

Рівняння виду M(x) N(y) dx+M(x) N(y) dy=0 називається рівнянням із змінними, що розділяються. Воно може бути приведене до рівняння з розділеними змінними шляхом ділення двох його частин на вираз

N(x) M(y):

або

Приклад 2. Знайти загальне рішення рівняння

; інтегруємо

In(y)=-In(x)+In(c) або In(y)= In

Загальне рішення y=c/x

Приклад 3. Знайти загальне рішення (1+x)ydx+(1-у)xdy= 0

; ;

In (x) +x + In (y)-y=C або In (xy) +x-y = C - загальне рішення

Приклад 4. Знайти загальне рішення .

Розділимо змінні, маємо , інтегруємо рівняння: .

Довільна стала С не може приймати будь – які числові значення , тому для подальшої зручності при перетвореннях замість С напишемо . Маємо - загальний розв’язок даного рівняння.

Приклад 5. Знайти часний розв’язок рівняння , задовольняючи початковим умовам S= 4, при t= π ∕3.

Це загальний розв’язок.

Для знаходження значення С , підставимо значення у вираз для загального розв’язку: , або .

Часний розв’язок має вигляд .

Приклад 6. Знайти загальне рішення

Приклад 7. Знайти загальне рішення

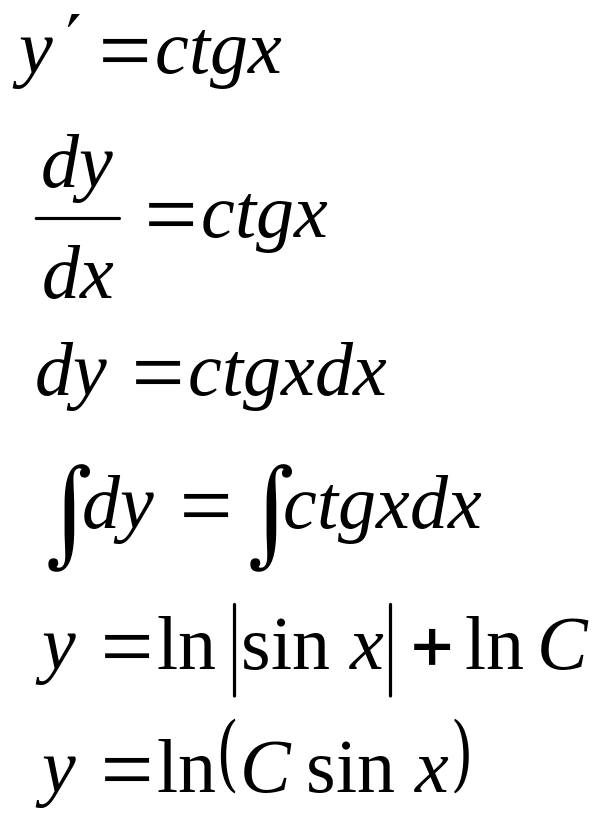
Приклад 8. Знайти загальне рішення

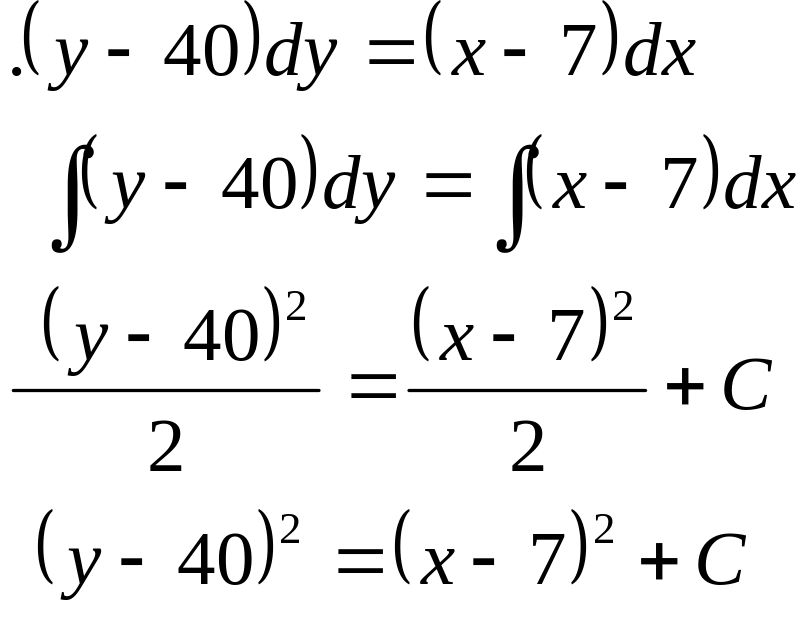
Приклад 9. Знайти загальне рішення.

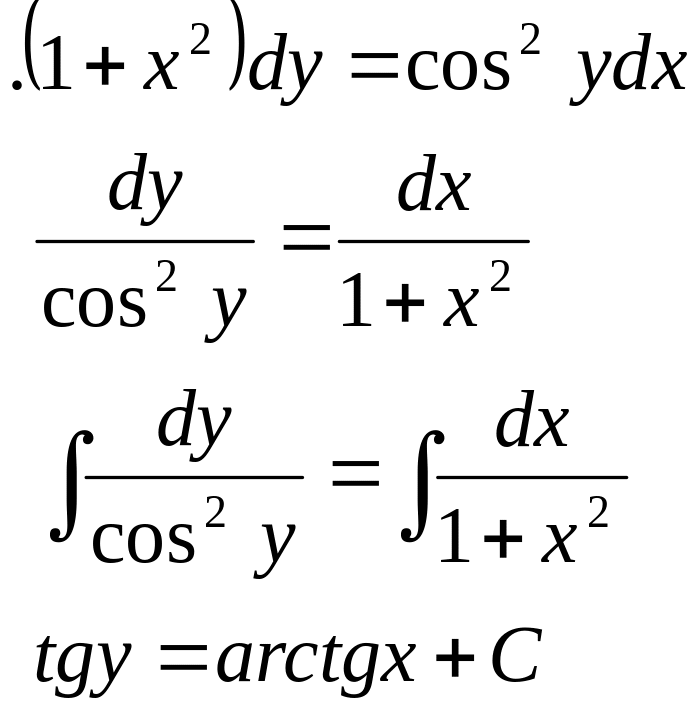
Приклад 10. Знайти загальне рішення

Приклад 11.

Приклад 12. Знайти часний розв’язок рівняння

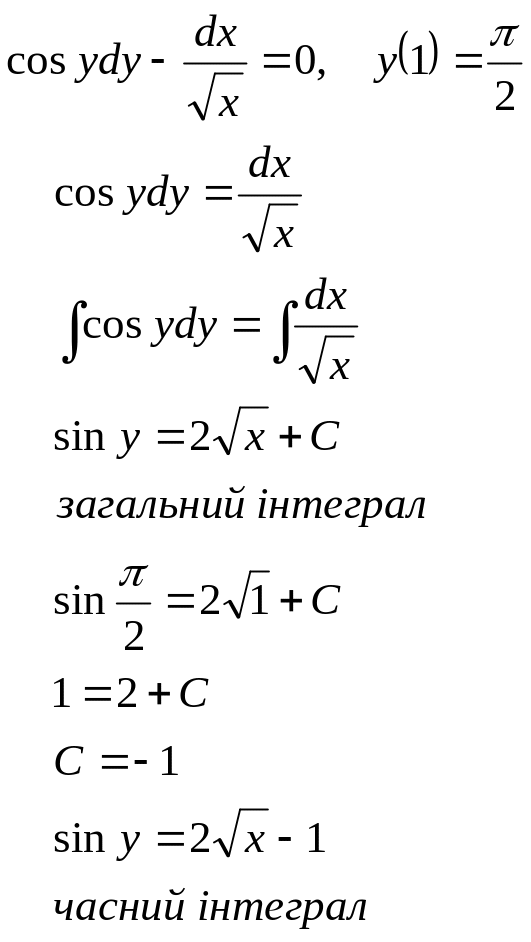
Приклад 13.

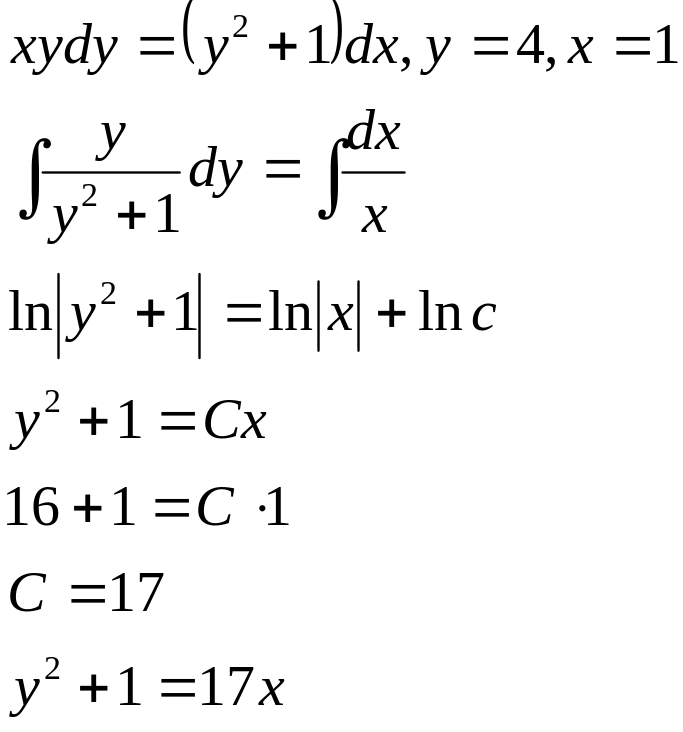
Приклад 14.