Непрерывность функции на отрезке
Функция
называется непрерывной
в интервале
(a,b), если она непрерывна в каждой точке
этого интервала.
Функция
называется непрерывной
на отрезке
[а,b], если она непрерывна в интервале
(a,b) и в точке
непрерывна справа (т.е.
),
а в точке x=b непрерывна слева (т. е.
).
Свойства функций, непрерывных на отрезке:
Если функция непрерывна на отрезке [a,b], то она ограниченна на этом отрезке.
Если функция непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения M (теорема Вейерштрасса).
Если функция непрерывна на отрезке [a,b] и значения её на концах отрезка
имеют противоположные знаки, то внутри
отрезка найдётся точка
,
такая что
(теорема
Больцано-Коши).
Определение непрерывности функции через приращение аргумента и функции.
Определение
непрерывности можно также сформулировать,
используя приращения аргумента и
функции. Функция является непрерывной
в точке 
,
если справедливо равенство
,
где
.
Теоремы о свойствах непрерывных функций.
Теорема 1.
Пусть
функция
непрерывна
в точке
,
и C является константой. Тогда
функция 
также
непрерывна при 
Теорема 2.
Даны
две функции 
непрерывные в точке
.
Тогда сумма этих функций 
также
непрерывна в точке
Теорема 3.
Предположим,
что две функции 
непрерывны
в точке
Тогда произведение этих функций
также
непрерывно в точке
Теорема 4.
Даны
две функции
непрерывные при
.
Тогда отношение этих функций 
также непрерывно при
при
условии, что
.
Теорема 5.
Предположим, что функция является дифференцируемой в точке . Тогда функция непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).
Теорема 6 (Теорема о предельном значении).
Если
функция
непрерывна
на закрытом и ограниченном интервале 
то она ограничена сверху и снизу на
данном интервале. Другими словами,
существуют числа 
,
такие, что
для
всех
в
интервале 
(смотрите
рисунок 1).
|
|
|
Рис.1 |
|
Рис.2
|
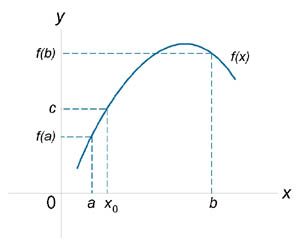
Теорема 7 (Теорема о промежуточном значении).
Пусть
функция
непрерывна
на закрытом и ограниченном интервале
.
Тогда, если 
−
некоторое число, большее 
и
меньшее 
то существует число
,
такое, что
.
Данная теорема
проиллюстрирована на рисунке 2.
Непрерывность основных элементарных функций в каждой точке, где они определены.
Все элементарные функции являются непрерывными в любой точке свой области определения.
Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
Алгебраические многочлены
;
Рациональные дроби
;
Степенные функции
;
Показательные функции
;
Логарифмические функции
;
Тригонометрические функции
;
Обратные тригонометрические функции
;
Гиперболические функции
;
Обратные гиперболические функции
.