Пункт 7.

Запишем выражения для комплексного вектора Пойнтинга для двух случаев: когда частота f принадлежит найденному в пункте 2 диапазону частот и когда она не принадлежит этому диапазону. Определим среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока.

Общая формула для расчета вектора Пойнтинга имеет следующий вид при

:

Где - это комплексная амплитуда напряженности электрического поля, а - это комплексно – сопряженная амплитуда напряженности магнитного поля, составляющие которой, были посчитаны ранее в пункте 2.

(47)

1. Рассмотрим первый случай (f>f_кр)

Преобразуем (47) подставив в него выражения (10), (16), (17).

Найдём выражения для каждой из составляющих вектора Пойнтинга:

Тогда выражение для вектора Пойнтинга примет вид:

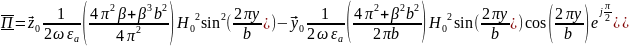(48)

Определим среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии, для этого возьмем действительную и мнимую части от (49) соответственно:

(49)

2. Рассмотрим второй случай (f<f_кр).

Подставим в выражение (47) выражения (15), (19) и (20).

Найдём выражения для каждой из составляющих вектора Пойнтинга:

Тогда выражение для вектора Пойнтинга примет вид:

(50)

В этом случае вектор Пойнтинга чисто мнимый и переноса энергии не происходит.

Пункт 8.

Вычислим средний за период поток энергии через поперечное сечение трубы.

Для этого проинтегрируем по площади поперечного сечения среднюю за период плотность потока энергии , определяемую выражением (49):

Где - это поперечное сечение волновода (рис.1), - элементарная площадка в этом поперечном сечении, - вектор указывающий направление распространения.

Представим :

Посчитаем интеграл отдельно:

Берем внутренний интеграл, независящий от переменной x.

Берем внешний интеграл:

Запишем окончательное выражение для среднего потока энергии с учетом посчитанного интеграла:

(51)

Подставим вычисленные ранее значения констант в (51) при f=f₁.

Средний поток энергии равен:

Вт (52)

Пункт 9.

Определим фазовую скорость и скорость распространения энергии рассматриваемой волны. Рассчитаем и построим графики зависимостей и от частоты.

Рассчитаем фазовую скорость волны с учетом м, где С – скорость света в среде.

(53)

На частоте f₁ :

Для расчета скорость распространения энергии воспользуемся соотношением [1]:

(54)

На частоте f₁:

Формулы (53) и (54) были запрограммированы в математическом пакете MathCAD 14, где были построены графики зависимостей V_ф и V_э от частоты. Результаты показаны на Рис. 17.

Рис.17

_{Из построенного графика видно, что Vф на граничной частоте стремится к бесконечности, а при увеличении частоты приближается к скорости света в данной среде. Vэ на граничной частоте стремится к нулю и переноса энергии не происходит. При увеличении частоты Vэ приближается к скорости света в данной среде. Таким образом, использования волновода на граничной частоте и близко к ней невозможно.}