Практическое занятие №7

Устойчивость систем управления. Частотные критерии

устойчивости

Цель: Получение практических навыков оценки устойчивости систем управления с использованием частотных критериев устойчивости

1.Исходные теоретические сведения

1.1. Частотные критерии устойчивости

Оценка устойчивости необходима для любой системы управления. Но даже для заведомо устойчивой системы необходимо знать степень ее устойчивости, т.е. определить ее относительную устойчивость.

Рассмотрим определение устойчивости системы по ее частотным характеристикам. Они могут быть рассчитаны по передаточной функции системы либо сняты экспериментально подачей на вход системы синусоидального сигнала и варьировании его частоты в заданном диапазоне.

Для определения устойчивости замкнутой системы алгебраическими методами необходимо исследовать ее характеристическое уравнение

.

Для устойчивости системы необходимо, чтобы все нули этого уравнения находились в левой части комплексной плоскости.

Найквистом было предложено отображать правую часть p-плоскости на , поэтому необходимо научиться отображать контуры на комплексной плоскости с помощью функции .

Отображение контуров на p-плоскости. Контур – некоторая замкнутая траектория на одной плоскости, отображаемая на другую плоскость соотношением . Поскольку p – комплексная переменная, , то - также комплексная функция, которую можно представить в виде и отобразить на -плоскости в координатах u и v.

Пример 1. Пусть и на p-плоскости имеется контур, представленный на рис. 1.

Рис.1. Контур на p-плоскости

Отсюда следует, что

.

Тогда

.

Таким образом, , , т.е. на -плоскости получим квадрат, сдвинутый на 1 вправо и имеющий длину стороны в два раза большую стороны исходного контура, как показано на рис.2.

Рис.2. Контур на -плоскости

Функция имеет нуль при , охватываемый исходным контуром на p-плоскости. На -плоскости ему соответствует точка с координатами

,

охватываемая также контуром отображения.

Пусть теперь отображающая функция имеет вид

,

тогда отображение исходного контура на -плоскость приобретает вид:

.

Отображение некоторых базовых точек исходного контура на -плоскость имеют значения, приведенные в табл. 1.

Таблица 1

Значения отображения базовых точек на -плоскость

Представление оригинала и его отображения	Базовая точка
	A	B	C	D

Контур отображения исходного квадрата на -плоскость приведен на рис. 3.

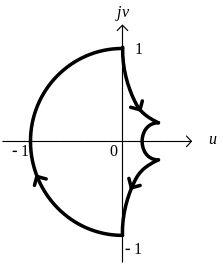
Рис.3. Отображение квадратного контура на -плоскость

С помощью функции

Функция имеет нуль при , не охватываемый

исходным контуром на p-плоскости. На -плоскости ему соответствует точка с координатами

,

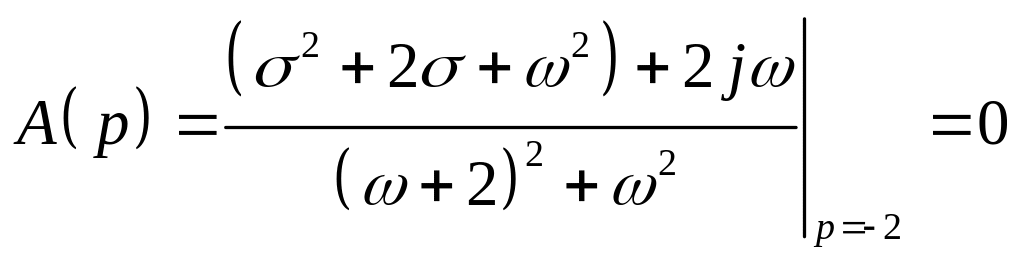также охватываемая контуром отображения.

■

Критерий Найквиста. Для исследования устойчивости усилителей с обратной связью Найквист в 1932 г. предложил критерий устойчивости, основанный на анализе частотных характеристик системы. Этот критерий был по-новому обоснован и применен для систем автоматического регулирования с дробно-рациональными передаточными функциями А. В. Михайловым в 1938 г. Для исследования устойчивости замкнутой системы регулирования, согласно этому критерию, необходимо знать амплитудно-фазовую частотную характеристику разомкнутой системы, которую можно получить как аналитически, так и экспериментально. Последнее обстоятельство выгодно отличает рассматриваемый критерий устойчивости от ранее изложенных. Заметим также, что критерий Найквиста имеет ясный физический смысл. Критерий Найквиста основан на теореме Коши, применяемой к функции с конечным числом полюсов и нулей, т.е. функции, которая может быть представлена в виде

.

Однако корнями характеристического уравнения являются нули функции и именно они определяют поведение системы во времени (нули функции на p-плоскости отображаются в начало координат -плоскости!). Охват исходным контуром корня на p-плоскости соответствует охвату начала координат контуром отображения на -плоскости. На этом основан принцип аргумента (охват начала координат на основе теоремы Коши): Если контур на p-плоскости при движении по нему по часовой стрелке охватывает (не совпадая!) Z нулей и P полюсов функции , то соответствующий контур на -плоскости охватывает начало координат раз также по часовой стрелке.

Так, в рассмотренном выше примере число нулей равно 1, а число полюсов равно 0, поэтому каждый контур отображения на -плоскости охватывает начало координат ровно 1 раз.

Пример 2. Для функции

отображение единичного квадрата на p-плоскости описывается как

.

При корне , охватываемом единичным контуром на p-плоскости, начало координат -плоскости не охватывается контуром отображения, как показано на рис. 4, поскольку минимальное значение полюса равно 0.5.

Рис. 4. Отображение квадратного контура на -плоскость

С помощью функции

■

Критерий Михайлова. В основе критерия Михайлова, сформулированного им в 1938 г., лежит известный в теории функций комплексного переменного принцип аргумента. Согласно этому принципу приращение аргумента функции f комплексного переменного р при изменении его по замкнутому контуру в положительном направлении (против часовой стрелки) составляет 2 ( N – P), где N – число нулей, а р – число полюсов функции f (р) внутри замкнутого контура. Предполагается, что функция f (р) аналитична внутри этого контура (кроме конечного числа полюсов) и не имеет нулей и полюсов на контуре.

Если применить принцип аргумента к характеристическому полиному А(р) замкнутой системы, то можно получить критерий Михайлова.

Согласно критерию Михайлова для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы годограф характеристического вектора А(j), начинаясь при =0 на действительной оси, с ростом  от 0 до  обходил последовательно в положительном направлении (против часовой стрелки) п квадрантов, где п – порядок характеристического уравнения.

Характеристический полином замкнутой системы можно представить в виде суммы К(р) и D (p). Отсюда следует, что для получения годографа А(j) необходимо построить годографы K(j) и D(j) и сложить векторы K(j) и D(j) для каждого значения . В случае, когда K(j) = k (k – коэффициент усиления системы), построение упрощается. Годограф A(j) получается простым смещением годографа D(j) вправо вдоль вещественной оси на величину k (рис. 4).

Заметим, что при повышении порядка системы (п>45) объем вычислений, связанных с применением критерия Михайлова, существенно возрастает. При использовании ЭВМ предпочтение отдают критерию Рауса.

Пусть передаточная функция разомкнутой системы регулирования . Образуем функцию

Числитель этой функции представляет собой характеристический полином замкнутой системы, знаменатель – характеристический полином разомкнутой системы. Пусть степень D(р) равна n, а степень K(р) равна m<n. Степень характеристического полинома замкнутой системы К(р)+D(р) также равна n.

Рассмотрим три случая состояния разомкнутой системы: устойчива, неустойчива и находится на границе устойчивости, причем в последнем случае характеристическое уравнение разомкнутой системы D(р)=0 имеет нулевой корень кратности , т. е.

Приведем формулировку критерия Найквиста для этого случая. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы W_p (j) при изменении  от 0 до  не охватывал точку (–1, j0).

II случай – система в разомкнутом состоянии неустойчива. При рассмотрении многоконтурных систем или одноконтурных систем, содержащих неустойчивые звенья, разомкнутая система может оказаться неустойчивой.

Пусть система в разомкнутом состоянии неустойчива, при этом характеристическое уравнение разомкнутой системы имеет l корней в правой полуплоскости.

Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы W_p (j) nри изменении  от 0 до  охватывал 1/2 раз в положительном направлении точку (–1, j0), где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Очевидно, что формулировка критерия Найквиста для первого случая является частным случаем (l = 0) только что приведенной формулировки.

III случай — система в разомкнутом состоянии находится на границе устойчивости.

Передаточная функция системы в разомкнутом состоянии

,

где  — число нулевых корней характеристического уравнения системы в разомкнутом состоянии; K(р) и D₁(p) — полиномы от р, причем D₁(р) не имеет нулей в правой полуплоскости и на мнимой оси.

Для устойчивости замкнутой системы автоматического регулирования, которая в разомкнутом состоянии находится на границе устойчивости, имея нулевые корни характеристического уравнения, необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы W_p(j), дополненный в бесконечности, при изменении  от 0 до  не охватывал точку (–1, j0).

Показанные на рис. 5 годографы соответствуют: на рис. 5 (б) – устойчивой системе; на рис. 5 (в) – неустойчивой системе; на рис. 5 (г) при  = 2 – устойчивой, а при  = 3 – неустойчивой системе.

Понятие «годограф, дополненный в бесконечности» означает, что после построения годографа разомкнутой системы мы мысленно дополняем его окружностью бесконечного радиуса, как показано на рис. 5 (в).

Понятие «охват точки (–1, j0)», используемое в приведенных выше формулировках критерия Найквиста, имеет некоторую неопределенность. Действительно, трудно сразу сказать, охватывает или не охватывает эту точку частотный годограф W_p(j), изображенный на рис. 5 (а). В сомнительных случаях можно прибегать к помощи формульных записей критерия Найквиста. Лучше, однако, дать критерию Найквиста иную формулировку, основанную на подсчете числа переходов частотного годографа W_p(j) через отрицательную действительную полуось при изменении его мнимой составляющей от –1 до –. Будем считать такой переход положительным, если при возрастании годограф переходит из верхней полуплоскости в нижнюю, и отрицательным, если

Рис. 5. Иллюстрация случаев критерия Найквиста для различных систем

годограф переходит из нижней полуплоскости в верхнюю (рис. 5).

Общая формулировка критерия Найквиста охватывает все три рассмотренных выше случая.

Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы разность между числами положительных и отрицательных переходов частотного годографа комплексного коэффициента передачи разомкнутой системы Wp(j) через отрицательную действительную полуось от –1 до – была равна l/2, где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Для систем, находящихся в разомкнутом состоянии на границе устойчивости с нулевыми корнями характеристического уравнения, число l считается равным нулю, а годограф Wp(j) берется с дополнением в бесконечности.

Показанный ранее на рис. 5, а годограф Wp(j) при l = 0 соответствует устойчивой замкнутой системе; на рис. 5, б показан годограф Wp(j) неустойчивой в разомкнутом состоянии системы, для которой l = 2. Годограф имеет два положительных перехода и один отрицательный переход, следовательно, разность между числами переходов равна единице. Согласно приведенной выше формулировке критерия устойчивости рассматриваемая система устойчива в замкнутом состоянии.