|
3.9
Унитарный(ортогональный) оператор.
Критерии унитарности.
Опр.
3.1
Линейный оператор
 ,
действующий в унитарном пространстве ,
действующий в унитарном пространстве
 (евклидовом пространстве
(евклидовом пространстве
 ),
называется унитарным (ортогональным),
если ),
называется унитарным (ортогональным),
если
 .
Квадратная матрица .
Квадратная матрица
 называется унитарной (ортогональной),
если
называется унитарной (ортогональной),
если
 . .
Из
определения вытекает:
1)
Если
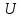 – унитарный ⟹
нормальный ⟹
выполняются все свойства нормального
оператора.
– унитарный ⟹
нормальный ⟹
выполняются все свойства нормального
оператора.
2)
 – унитарный ⟺
в любом ОНБ
– унитарный ⟺
в любом ОНБ
 - унитарна.
- унитарна.
∎ В
ОНБ
 . .
 -
унитарна ⟺
-
унитарна ⟺
 ⟺
по теореме 1.5 в ОНБ
⟺
по теореме 1.5 в ОНБ
 ⟺
⟺
 .
∎ .
∎
Теорема
3.1
(Критерий унитарности)
В
конечномерном унитарном (евклидовом)
пространстве
 следующие утверждения равносильны:
следующие утверждения равносильны:
1)
 - унитаный (ортогональный);
- унитаный (ортогональный);
2)
 ; ;
3)
 ; ;
4)
 - сохраняет скалярное произведение;
- сохраняет скалярное произведение;
5)
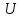 - сохраняет длину, т.е.
- сохраняет длину, т.е.
 ; ;
6)
 переводит ОНБ в ОНБ.
переводит ОНБ в ОНБ.
∎ 1)
⟹2),
1) ⟹
3) – очевидно.
2)
⟹1)
 ⟹
⟹
 -
невырожденный ⟹
-
невырожденный ⟹
 ⟹ 1).
⟹ 1).
3)
⟹ 1) аналогично.
1)
⟹ 4)
 . .
4)
⟹
1)
 . .
4)
⟹
5)
 . .
5)
⟹
4) (п.9, раздел 2):
 . .
4)
⟹
6)
Пусть
 - ОНБ
- ОНБ
 , ,
 ⟹
⟹
 – ОНБ
– ОНБ . .
6)
⟹
4)
Пусть
ОНБ
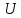
 в ОНБ
в ОНБ
 , ,
 : :
 .
∎ .
∎
Следствие
1.
 – унитарен ⟺
– унитарен ⟺
 - унитарен.
- унитарен.
Следствие
2.
 -
унитарные операторы ⟹ -
унитарные операторы ⟹
 - унитарный.
- унитарный.
∎ 1)
 ⟹
⟹
 - унитарный.
- унитарный.
 ⟹
⟹
 -
унитарный.
-
унитарный.
2)
 ⟹ ⟹
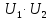 - унитарный.
- унитарный.
|
3.10
Унитарные(ортогональные) матрицы,
св-ва. Матрица перехода от ОНБ к ОНБ.
Теорема
3.2
(Свойства унитарных (ортогональных)
матриц)
Пусть
 - унитарная (ортогональная) матрица,
т.е.
- унитарная (ортогональная) матрица,
т.е.
 ,
тогда ,
тогда
1)
 ; ;
2)
 ; ;
3)
столбцы (строки) матрицы
 образуют ОНБ пространства
образуют ОНБ пространства
 . .
∎ 1)
⟸
из определения обратной и унитарной
матриц.
2)
 . .
3)
 , ,
 ⟺
⟺
 , ,
 ⟹
строки
(столбцы) образуют ОНБ в арифметическом
пространстве ⟹
строки
(столбцы) образуют ОНБ в арифметическом
пространстве
 .
∎ .
∎
Лемма
3.3
Условие
3) является не только необходимым, но
и достаточным условием, т.е.
 - унитарная матрица ⟺
строки (столбы) образуют ОНБ в
арифметическом пространстве
- унитарная матрица ⟺
строки (столбы) образуют ОНБ в
арифметическом пространстве
 . .
∎ «⟸» .
Положим .
Положим
 : :
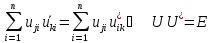 , ,
 .
Положим .
Положим
 : :
 . .
⟹
 -
унитарна. ∎
-
унитарна. ∎
Следствие.
Матрица
перехода от одного ОНБ к другому ОНБ
в унитарном (евклидовом) пространстве
унитарна (ортогональна).
∎
 – ОНБ,
– ОНБ,
 ,
т.к. обратная матрица единственна, то ,
т.к. обратная матрица единственна, то
 .
Следовательно, .
Следовательно,
 - унитарная матрица. ∎
- унитарная матрица. ∎
|
3.11
Спектральная теорема для нормальных
операторов и матриц.
Теорема
4.1
1)
Линейный оператор
 ,
действующий в унитарном
пространстве ,
действующий в унитарном
пространстве
 есть нормальный оператор ⟺
для него существует базис из собственных
векторов.
есть нормальный оператор ⟺
для него существует базис из собственных
векторов.
2)
Матрица
 - нормальная матрица ⟺
существует унитарная матрица
- нормальная матрица ⟺
существует унитарная матрица
 ,
столбцами которой являются собственные
векторы матрицы ,
столбцами которой являются собственные
векторы матрицы
 ,
приводящая матрицу в диагональному
виду: ,
приводящая матрицу в диагональному
виду:
 . .
∎ 1)
«⟹»
Пусть
 - нормальный оператор.
- нормальный оператор.
 -
характеристический многочлен оператора
(совпадает с характеристическим
многочленом матрицы этого оператора
в произвольном базисе). Характеристический
многочлен
-
характеристический многочлен оператора
(совпадает с характеристическим
многочленом матрицы этого оператора
в произвольном базисе). Характеристический
многочлен
 имеет хотя бы один корень
имеет хотя бы один корень
 ,
следовательно, существует хотя бы
один собственный вектор ,
следовательно, существует хотя бы
один собственный вектор
 .
Пусть .
Пусть
 и
и
 .
Тогда по Т 2.1(п.5) .
Тогда по Т 2.1(п.5)
 - инвариантно относительно
- инвариантно относительно
 . .
Рассмотрим

Продолжим
процесс:
 ,
где ,
где
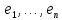 - ортонормированная система векторов,
они образуют ОНБ в
- ортонормированная система векторов,
они образуют ОНБ в
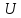 . .
«⟸»
Оператор
 имеет ОНБ из собственных векторов.
Тогда матрица оператора
имеет ОНБ из собственных векторов.
Тогда матрица оператора
 в этом базисе имеет диагональный вид.
Тогда
в этом базисе имеет диагональный вид.
Тогда
 тоже имеет диагональный вид и
тоже имеет диагональный вид и
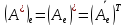 .
Диагональные матрицы перестановочны
⟹ .
Диагональные матрицы перестановочны
⟹
 ⟹
перестановочны операторы
⟹
перестановочны операторы
 ⟹
⟹
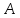 - нормальный оператор.
- нормальный оператор.
2)
«⟹»
Пусть
 - нормальная матрица:
- нормальная матрица:
 ; ;
 -
произвольный ОНБ
-
произвольный ОНБ
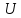 ; ;
 -
нормальный оператор:
-
нормальный оператор:
 . .
Из
1) ⟹
 ОНБ из собственных векторов
ОНБ из собственных векторов
 оператора
оператора
 и
и
 имеет в
имеет в
 диагональный вид:
диагональный вид:
 . .
 -
матрица перехода от одного ОНБ к
другому ОНБ ⟹
-
матрица перехода от одного ОНБ к
другому ОНБ ⟹
 - унитарная матрица:
- унитарная матрица:
 ⟹
⟹
 . .
«⟸»
Пусть
 ,
где ,
где
 - унитарная матрица.
- унитарная матрица.
 . .
Докажем,
что
 - нормальная матрица.
- нормальная матрица.
 , ,
 , ,
 . .
 -
диагональная матрица:
-
диагональная матрица:
 - нормальная матрица. ∎
- нормальная матрица. ∎
|
3.12
Самосопряженные операторы, св-ва.
Эрмитовые (симметрические) матрицы.
Опр.
5.1
Линейный
оператор
 ,
действующий в унитарном (евклидовом)
пространстве называется самосопряженным,
если ,
действующий в унитарном (евклидовом)
пространстве называется самосопряженным,
если
 .
Самосопряженный оператор в унитарном
пространстве называют эрмитовым,
в евклидовом – симметрическим.
Квадратная матрица .
Самосопряженный оператор в унитарном
пространстве называют эрмитовым,
в евклидовом – симметрическим.
Квадратная матрица
 называется самосопряженной,
если
называется самосопряженной,
если
 ,
т.е. ,
т.е.
 .
Комплексную самосопряженную матрицу
называют эрмитовой,
вещественную – симметрической. .
Комплексную самосопряженную матрицу
называют эрмитовой,
вещественную – симметрической.
Теорема
5.1
(свойства самосопряженных операторов)
1)
Самосопряженный оператор – нормальный
(⟹
удовлетворяет свойствам нормальных
операторов Т2.1).
2)
Все собственные значения самосопряженного
оператора вещественны.
3)
 - самосопряженный оператор ⟺
в любом ОНБ
- самосопряженный оператор ⟺
в любом ОНБ
 - эрмитова матрица.
- эрмитова матрица.
4)
 . .
∎ 1)
 ⟹
⟹
 - нормальный оператор.
- нормальный оператор.
2)
 . .
3)
 - эрмитова матрица, т.е.
- эрмитова матрица, т.е.
 ⟺
в любом ОНБ
⟺
в любом ОНБ
 . .
4)
 .
∎ .
∎
|
3.13
Связь между нормальным, самосопряженным
и унитарным оператором.
Теорема
5.2
1)
 – самосопряженный оператор ⟺
– самосопряженный оператор ⟺
 - нормальный оператор и все собственные
значения этого оператора вещественны.
- нормальный оператор и все собственные
значения этого оператора вещественны.
2)
𝒰
- унитарный оператор ⟺
𝒰
– нормальный оператор и все собственные
значения по модулю равны единицы, т.е.

∎ 1)
«⟹»
Т 5.1
«⟸»
 - нормальный оператор;
- нормальный оператор;
 . .
Из
основной спектральной теоремы ⟹
существует ОНБ из собственных векторов:
 . .
 , ,
 . .
2)
«⟹»
 - унитарный ⟹
- унитарный ⟹
 – нормальный.
– нормальный.
 . .
«⟸»
𝒰
– нормальный оператор и
 существует ОНБ из собственных векторов:
существует ОНБ из собственных векторов:
 . .
 ⟹ ⟹
 – унитарный.
∎
– унитарный.
∎
|
|
3.14
Спектральная теорема для самомопряженных
операторов и эрмитовых (симметрич.)
матриц
Теорема
6.1
Линейный
оператор, действующий в унитарном
пространстве
 самосопряжен ⟺
существует ОНБ из собственных векторов
и все собственные значения – вещественны.
самосопряжен ⟺
существует ОНБ из собственных векторов
и все собственные значения – вещественны.
∎ «⟹»
 - самосопряженный ⟹
по Т5.2
- самосопряженный ⟹
по Т5.2
 - нормальный и
- нормальный и
 ⟹
по Т4.1
(основная спектральная теорема)
существует ОНБ из собственных векторов.
⟹
по Т4.1
(основная спектральная теорема)
существует ОНБ из собственных векторов.
«⟸»
Существует ОНБ из собственных векторов
⟹ по Т4.1
 - нормальный и
- нормальный и
 ⟹𝒜
– самосопряженный. ∎
⟹𝒜
– самосопряженный. ∎
Теорема
6.2
Матрица
 - эрмитова ⟺ все собственные
значения
матрицы
- эрмитова ⟺ все собственные
значения
матрицы
 вещественны и существует унитарная
матрица
вещественны и существует унитарная
матрица
 ,
столбцы которой – собственные векторы
матрицы ,
столбцы которой – собственные векторы
матрицы
 ,
отвечающие собственным значениям ,
отвечающие собственным значениям
 . .
∎ -
эрмитова матрица ⟺
для любого ОНБ -
эрмитова матрица ⟺
для любого ОНБ
 - самосопряжен ⟺
- самосопряжен ⟺
 - нормален и
- нормален и
 ⟺
⟺ - нормальная матрица и
- нормальная матрица и
 ⟺
⟺
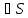 –
унитарная матрица –
унитарная матрица .
∎ .
∎
Замечание.
Теоремы 6.1, 6.2 верны и для евклидова
пространства.
Теорема
6.3
 - унитарный ⟺ существует ОНБ из
собственных векторов и
- унитарный ⟺ существует ОНБ из
собственных векторов и
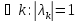 . .
∎ «⟹» – унитарный ⟹
– унитарный ⟹
 - нормальный и
- нормальный и
 ⟹ существует ОНБ из собственных
векторов.
⟹ существует ОНБ из собственных
векторов.
«⟸»
Существует ОНБ из собственных векторов
⟹
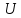 - нормальный и
- нормальный и
 ⟹
⟹
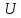 – унитарный. ∎
– унитарный. ∎
|
3.15
Спектральная теорема для унитарных
операторов и унитарных матриц
Теорема
6.3
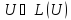 -
унитарный ⟺ существует ОНБ из
собственных векторов и
-
унитарный ⟺ существует ОНБ из
собственных векторов и
 . .
∎ «⟹» – унитарный ⟹
– унитарный ⟹
 - нормальный и
- нормальный и
 ⟹ существует ОНБ из собственных
векторов.
⟹ существует ОНБ из собственных
векторов.
«⟸»
Существует ОНБ из собственных векторов
⟹
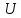 - нормальный и
- нормальный и
 ⟹
⟹
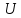 – унитарный. ∎
– унитарный. ∎
Теорема
6.4
Матрица
 - унитарна ⟺ существует унитарная
матрица
- унитарна ⟺ существует унитарная
матрица
 . .
∎ -
унитарна ⟺ в любом ОНБ
-
унитарна ⟺ в любом ОНБ
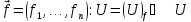 - унитарный оператор ⟺
- унитарный оператор ⟺
 - нормальный и
- нормальный и
 ⟺ существует унитарная матрица
⟺ существует унитарная матрица
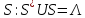 .∎ .∎
|
3.16
Положительно определенные операторы.
Представление невырожденного оператора
в виде произведения самосопряженного
и унитарного операторов.
Определение
8.1
Самосопряженный оператор
 называется положительно определенным,
если для
называется положительно определенным,
если для
 и неотрицательно определенным, если
и неотрицательно определенным, если
 . .
Пусть
в
 задан ОНБ:
задан ОНБ:
 ,
тогда ,
тогда
 - эрмитова квадратичная форма от
переменных
- эрмитова квадратичная форма от
переменных
 ,
причем, если ,
причем, если
 - положительно определен, то
- положительно определен, то
 положительно определена (аналогично
для неотрицательно определенного
оператора
положительно определена (аналогично
для неотрицательно определенного
оператора
 ). ).
Теорема
8.1
 - самосопряженный оператор является
положительно определенным (неотрицательно
определенным) ⟺
все его собственные значения положительны
(неотрицательны):
- самосопряженный оператор является
положительно определенным (неотрицательно
определенным) ⟺
все его собственные значения положительны
(неотрицательны):
 . .
∎
 -
самосопряженный оператор ⟺
существует ОНБ из собственных векторов
и
-
самосопряженный оператор ⟺
существует ОНБ из собственных векторов
и
 .
∎ .
∎
Пусть
 – положительно определенный оператор
(неотрицательно определенный),
существует ОНБ из собственных векторов
– положительно определенный оператор
(неотрицательно определенный),
существует ОНБ из собственных векторов
 и
и
 .
Положим .
Положим
 и определим линейный оператор
и определим линейный оператор
 ⟹
⟹
 - самосопряженный оператор,
- самосопряженный оператор,
 ,
и ,
и
 положительно определенный (неотрицательно
определенный).
положительно определенный (неотрицательно
определенный).
Определение
8.2
Положительно определенный оператор
 ,
связанный с ,
связанный с
 равенством
равенством
 ,
называется арифметическим корнем из
оператора ,
называется арифметическим корнем из
оператора
 и обозначается
и обозначается
 . .
Теорема
8.2
Для любого
 есть неотрицательно определенный
оператор и, если
есть неотрицательно определенный
оператор и, если
 - невырожденный, то и
- невырожденный, то и
 - невырожденный оператор.
- невырожденный оператор.
∎ 1) ⟹
⟹
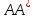 - самосопряженный оператор;
- самосопряженный оператор;
 ⟹
неотрицательно определенный оператор.
⟹
неотрицательно определенный оператор.
2)
Пусть
 - невырожденный ⟺
- невырожденный ⟺
 - обратим ⟹
матрица оператора
- обратим ⟹
матрица оператора
 в любом базисе невырожденная ⟹
в любом ОНБ
в любом базисе невырожденная ⟹
в любом ОНБ
 ⟹
⟹
 - невырожденная ⟹
оператор
- невырожденная ⟹
оператор
 невырожденный
⟹
оператор
невырожденный
⟹
оператор
 невырожденный. ∎
невырожденный. ∎
Теорема
8.3
Всякий невырожденный линейный оператор
 может быть представлен в виде
может быть представлен в виде
 (или
(или
 ),
где ),
где
 - положительно определенный оператор,
- положительно определенный оператор,
 - унитарный оператор.
- унитарный оператор.
∎ Пусть
 - невырожденный оператор ⟹
- невырожденный оператор ⟹
 невырожденный положительно определенный
оператор. Положим
невырожденный положительно определенный
оператор. Положим
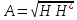 ⟹
⟹
 невырожденный положительно определенный
оператор. Положим
невырожденный положительно определенный
оператор. Положим
 .
Покажем, что .
Покажем, что
 – унитарный:
– унитарный:
 (
( положительно определенный ⟹
самосопряженный). ∎
положительно определенный ⟹
самосопряженный). ∎
|
3.17
Приведение эрмитовой квадратичной
формы к каноническому виду
Пусть
в унитарном (евклидовом) пространстве
 задана эрмитова квадратичная форма
задана эрмитова квадратичная форма
 . .
Теорема
7.1
Любая эрмитова квадратичная форма
 с матрицей
с матрицей
 при помощи некоторого унитарного
преобразования переменных
при помощи некоторого унитарного
преобразования переменных
 ,
где ,
где
 - унитарная матрица, может быть
приведена к каноническому виду:
- унитарная матрица, может быть
приведена к каноническому виду:
 ,
где ,
где
 и с точностью до порядка определены
матрицей
и с точностью до порядка определены
матрицей
 однозначно (они совпадают с собственными
значениями матрицы
однозначно (они совпадают с собственными
значениями матрицы
 ).
Столбцы унитарной матрицы ).
Столбцы унитарной матрицы
 -
нормированные собственные векторы
матрицы -
нормированные собственные векторы
матрицы
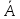 ,
отвечающие собственным значениям ,
отвечающие собственным значениям
 . .
∎ Рассмотрим
полярную полуторалинейную форму
 к эрмитовой форме
к эрмитовой форме
 . .
 определена однозначно (п.9, раздел 2).
Для любой
определена однозначно (п.9, раздел 2).
Для любой
 существует
единственный линейный оператор существует
единственный линейный оператор
 и в любом ОНБ
и в любом ОНБ
 (п.7,
раздел 3). (п.7,
раздел 3).
 - эрмитова полуторалинейная форма ⟺
- эрмитова полуторалинейная форма ⟺
 ⟹
⟹
 ,
т.е. ,
т.е.
 ⟹
⟹
 -
самосопряженный оператор: -
самосопряженный оператор:
 . .
Рассмотрим
 .
Согласно спектральной теореме для
самосопряженных операторов (Т6.1)
существует ОНБ из собственных векторов
оператора .
Согласно спектральной теореме для
самосопряженных операторов (Т6.1)
существует ОНБ из собственных векторов
оператора

 . .
 . .
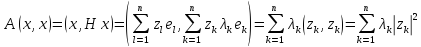 . .
Матрица
 унитарна, как матрица перехода от
одного ОНБ к другому ОНБ. Рассмотрим
матрицу
унитарна, как матрица перехода от
одного ОНБ к другому ОНБ. Рассмотрим
матрицу
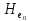 : :
 .
⟹ .
⟹ . ∎
. ∎
Замечание.
В евклидовом пространстве:
 . .
|
3.18
Одновр. приведение к канонич. виду
пары квадр. форм
 и
и
 эрмитовы квадратич. формы
эрмитовы квадратич. формы
 .
Найдем невырожденное преобразование
координат, одновременно приводящее
эрмитовы квадратич. формы к канонич.
виду. .
Найдем невырожденное преобразование
координат, одновременно приводящее
эрмитовы квадратич. формы к канонич.
виду.
Теор.9.1
(достаточное условие разрешимости
поставленной задачи)
Пусть
 и
и
 эрмитовы квадратичные формы в
комплексном пространстве, причем
эрмитовы квадратичные формы в
комплексном пространстве, причем
 .
Тогда существует базис .
Тогда существует базис
 ,
в котором ,
в котором
 и
и
 имеют канонич. вид:
имеют канонич. вид:
 где где
 . .
∎ Рассм.
полуторалинейную форму
 ,
полярную к эрмитовой квадратич. форме ,
полярную к эрмитовой квадратич. форме
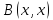 .
В .
В
 введем скалярное произведение с
помощью
введем скалярное произведение с
помощью
 .
Рассм. .
Рассм.
 с введенным скалярным произведением
– это унитарное пространство. Тогда
сущ. унитарное преобразование (п.7),
приводящее эрмитову квадратич. форму
к канонич. виду:
с введенным скалярным произведением
– это унитарное пространство. Тогда
сущ. унитарное преобразование (п.7),
приводящее эрмитову квадратич. форму
к канонич. виду:
 .
Т.к. .
Т.к.
 – унитарная матрица (⟺
матрица перехода от одного ОНБ к
другому ОНБ) ⟹
– унитарная матрица (⟺
матрица перехода от одного ОНБ к
другому ОНБ) ⟹
 - ОНБ и
- ОНБ и
 , где
, где
 .∎ .∎
Опр.
9.1
Пучком
квадратич. форм, определенным парой
 и
и
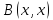 ,
называется совокупность форм ,
называется совокупность форм
 ,
где ,
где
 - параметр. Если
- параметр. Если
 ,
то пучок называется регулярным. ,
то пучок называется регулярным.
Опр
9.2
Пусть
 и
и
 - матрицы
- матрицы
 и
и
 в некотором базисе. Уравнение
в некотором базисе. Уравнение
 называется характеристическим
уравнением пучка
называется характеристическим
уравнением пучка
 . .
Если
 - какой-нибудь корень характеристич.
уравнения, то
- какой-нибудь корень характеристич.
уравнения, то
 . .
Опр
9.3
Число
 ,
удовлетв. характеристич.уравнению
пучка, называется собственным значением
пучка, ,
удовлетв. характеристич.уравнению
пучка, называется собственным значением
пучка,
 называется главным вектором пучка.
называется главным вектором пучка.
Теор
9.2
Пусть
 и
и
 - эрмитовы квадратич. формы,
- эрмитовы квадратич. формы,
 .
Тогда существует невырожденное
преобразование: .
Тогда существует невырожденное
преобразование:
 с матрицей
с матрицей
 ,
где ,
где
 - главные векторы – столбцы пучка
- главные векторы – столбцы пучка
 ,
ормированные в смысле скалярного
произведения ,
ормированные в смысле скалярного
произведения
 (
( - полярная полуторалинейная форма к
эрмитовой форме
- полярная полуторалинейная форма к
эрмитовой форме
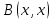 ),
т.е. ),
т.е.
 ,
приводящее эрмитовы квадратич. формы
к канонич.виду: ,
приводящее эрмитовы квадратич. формы
к канонич.виду: , ,
 - собственные значения пучка
- собственные значения пучка
 ,
соответствующие столбцам матрицы ,
соответствующие столбцам матрицы
 . .
Замеч.
Теорема
9.2 сформулирована для эрмитовых
квадратичных форм. Док-во проведем
для квадратичных форм в евклидовом
пространстве.
∎1)
Покажем, что все
 пучка
пучка
 вещественны и им соответствует
вещественны и им соответствует
 линейно независимых главных векторов
линейно независимых главных векторов
 : :
 ,
которые могут быть выбраны так, что ,
которые могут быть выбраны так, что
 . .
Рассмотрим
 .
Обозначим .
Обозначим
 Т.к.
Т.к.
 – положительно определенная квадратичная
форма ⟹
матрица
– положительно определенная квадратичная
форма ⟹
матрица
 – положительно определена. Рассмотрим
матрицу
– положительно определена. Рассмотрим
матрицу
 : : . .


 , ,
но
 - симметрические матрицы ⟹
- симметрические матрицы ⟹
 - симметрическая ⟹
существует ортогональная матрица,
столбцами которой являются собственные
векторы-столбцы матрицы
- симметрическая ⟹
существует ортогональная матрица,
столбцами которой являются собственные
векторы-столбцы матрицы
 и
и
 . .
Док.,
что
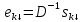 - собственный вектор матрицы
- собственный вектор матрицы
 . .
Подействуем
 ,
т.е. ,
т.е.
 – собственный вектор матрицы
– собственный вектор матрицы
 и
и
 .
Векторы .
Векторы
 могут быть выбраны так, что:
могут быть выбраны так, что:

 .2)
Рассмотрим .2)
Рассмотрим
 .
Покажем, что .
Покажем, что
 : :
 .∎ .∎
|


 ,
действующий в унитарном пространстве
,
действующий в унитарном пространстве
 (евклидовом пространстве
(евклидовом пространстве
 ),
называется унитарным (ортогональным),
если
),
называется унитарным (ортогональным),
если
 .
Квадратная матрица
.
Квадратная матрица
 называется унитарной (ортогональной),
если
называется унитарной (ортогональной),
если
 .
.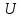 – унитарный ⟹
нормальный ⟹
выполняются все свойства нормального
оператора.
– унитарный ⟹
нормальный ⟹
выполняются все свойства нормального
оператора. – унитарный ⟺
в любом ОНБ
– унитарный ⟺
в любом ОНБ
 - унитарна.
- унитарна. .
. -
унитарна ⟺
-
унитарна ⟺
 ⟺
по теореме 1.5 в ОНБ
⟺
по теореме 1.5 в ОНБ
 ⟺
⟺
 .
∎
.
∎ следующие утверждения равносильны:
следующие утверждения равносильны: - унитаный (ортогональный);
- унитаный (ортогональный); ;
; ;
; - сохраняет скалярное произведение;
- сохраняет скалярное произведение;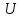 - сохраняет длину, т.е.
- сохраняет длину, т.е.
 ;
; переводит ОНБ в ОНБ.
переводит ОНБ в ОНБ. ⟹
⟹
 -
невырожденный ⟹
-
невырожденный ⟹
 ⟹ 1).
⟹ 1). .
. .
. .
. .
. - ОНБ
- ОНБ
 ,
, ⟹
⟹
 – ОНБ
– ОНБ .
.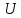
 в ОНБ
в ОНБ
 ,
,
 :
: .
∎
.
∎ – унитарен ⟺
– унитарен ⟺
 - унитарен.
- унитарен. -
унитарные операторы ⟹
-
унитарные операторы ⟹
 - унитарный.
- унитарный. ⟹
⟹
 - унитарный.
- унитарный. ⟹
⟹
 -
унитарный.
-
унитарный. ⟹
⟹
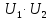 - унитарный.
- унитарный. - унитарная (ортогональная) матрица,
т.е.
- унитарная (ортогональная) матрица,
т.е.
 ,
тогда
,
тогда ;
; ;
; образуют ОНБ пространства
образуют ОНБ пространства
 .
. .
. ,
, ⟺
⟺
 ,
, ⟹
строки
(столбцы) образуют ОНБ в арифметическом
пространстве
⟹
строки
(столбцы) образуют ОНБ в арифметическом
пространстве
 .
∎
.
∎ - унитарная матрица ⟺
строки (столбы) образуют ОНБ в
арифметическом пространстве
- унитарная матрица ⟺
строки (столбы) образуют ОНБ в
арифметическом пространстве
 .
. .
Положим
.
Положим
 :
:
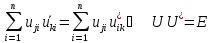 ,
,
 .
Положим
.
Положим
 :
:
 .
.
 -
унитарна. ∎
-
унитарна. ∎ – ОНБ,
– ОНБ, ,
т.к. обратная матрица единственна, то
,
т.к. обратная матрица единственна, то
 .
Следовательно,
.
Следовательно,
 - унитарная матрица. ∎
- унитарная матрица. ∎ ,
действующий в унитарном
пространстве
,
действующий в унитарном
пространстве
 есть нормальный оператор ⟺
для него существует базис из собственных
векторов.
есть нормальный оператор ⟺
для него существует базис из собственных
векторов. - нормальная матрица ⟺
существует унитарная матрица
- нормальная матрица ⟺
существует унитарная матрица
 ,
столбцами которой являются собственные
векторы матрицы
,
столбцами которой являются собственные
векторы матрицы
 ,
приводящая матрицу в диагональному
виду:
,
приводящая матрицу в диагональному
виду:
 .
. - нормальный оператор.
- нормальный оператор.
 -
характеристический многочлен оператора
(совпадает с характеристическим
многочленом матрицы этого оператора
в произвольном базисе). Характеристический
многочлен
-
характеристический многочлен оператора
(совпадает с характеристическим
многочленом матрицы этого оператора
в произвольном базисе). Характеристический
многочлен
 имеет хотя бы один корень
имеет хотя бы один корень
 ,
следовательно, существует хотя бы
один собственный вектор
,
следовательно, существует хотя бы
один собственный вектор
 .
Пусть
.
Пусть
 и
и
 .
Тогда по Т 2.1(п.5)
.
Тогда по Т 2.1(п.5)
 - инвариантно относительно
- инвариантно относительно
 .
.
 ,
где
,
где
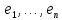 - ортонормированная система векторов,
они образуют ОНБ в
- ортонормированная система векторов,
они образуют ОНБ в
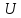 .
. имеет ОНБ из собственных векторов.
Тогда матрица оператора
имеет ОНБ из собственных векторов.
Тогда матрица оператора
 в этом базисе имеет диагональный вид.
Тогда
в этом базисе имеет диагональный вид.
Тогда
 тоже имеет диагональный вид и
тоже имеет диагональный вид и
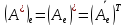 .
Диагональные матрицы перестановочны
⟹
.
Диагональные матрицы перестановочны
⟹
 ⟹
перестановочны операторы
⟹
перестановочны операторы
 ⟹
⟹
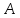 - нормальный оператор.
- нормальный оператор. - нормальная матрица:
- нормальная матрица:
 ;
; -
произвольный ОНБ
-
произвольный ОНБ
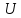 ;
; -
нормальный оператор:
-
нормальный оператор:
 .
. ОНБ из собственных векторов
ОНБ из собственных векторов
 оператора
оператора
 и
и
 имеет в
имеет в
 диагональный вид:
диагональный вид:
 .
. -
матрица перехода от одного ОНБ к
другому ОНБ ⟹
-
матрица перехода от одного ОНБ к
другому ОНБ ⟹
 - унитарная матрица:
- унитарная матрица:
 ⟹
⟹
 .
. ,
где
,
где
 - унитарная матрица.
- унитарная матрица.
 .
. - нормальная матрица.
- нормальная матрица.
 ,
, ,
, .
. -
диагональная матрица:
-
диагональная матрица:
 - нормальная матрица. ∎
- нормальная матрица. ∎ ,
действующий в унитарном (евклидовом)
пространстве называется самосопряженным,
если
,
действующий в унитарном (евклидовом)
пространстве называется самосопряженным,
если
 .
Самосопряженный оператор в унитарном
пространстве называют эрмитовым,
в евклидовом – симметрическим.
Квадратная матрица
.
Самосопряженный оператор в унитарном
пространстве называют эрмитовым,
в евклидовом – симметрическим.
Квадратная матрица
 называется самосопряженной,
если
называется самосопряженной,
если
 ,
т.е.
,
т.е.
 .
Комплексную самосопряженную матрицу
называют эрмитовой,
вещественную – симметрической.
.
Комплексную самосопряженную матрицу
называют эрмитовой,
вещественную – симметрической.
 - самосопряженный оператор ⟺
в любом ОНБ
- самосопряженный оператор ⟺
в любом ОНБ
 - эрмитова матрица.
- эрмитова матрица. .
. ⟹
⟹
 - нормальный оператор.
- нормальный оператор. .
. - эрмитова матрица, т.е.
- эрмитова матрица, т.е.
 ⟺
в любом ОНБ
⟺
в любом ОНБ
 .
. .
∎
.
∎ – самосопряженный оператор ⟺
– самосопряженный оператор ⟺
 - нормальный оператор и все собственные
значения этого оператора вещественны.
- нормальный оператор и все собственные
значения этого оператора вещественны.
 - нормальный оператор;
- нормальный оператор;
 .
.
 .
. ,
, .
. - унитарный ⟹
- унитарный ⟹
 – нормальный.
– нормальный.
 .
. существует ОНБ из собственных векторов:
существует ОНБ из собственных векторов:
 .
. ⟹
⟹
 – унитарный.
∎
– унитарный.
∎ самосопряжен ⟺
существует ОНБ из собственных векторов
и все собственные значения – вещественны.
самосопряжен ⟺
существует ОНБ из собственных векторов
и все собственные значения – вещественны. - самосопряженный ⟹
по Т5.2
- самосопряженный ⟹
по Т5.2
 - нормальный и
- нормальный и
 ⟹
по Т4.1
(основная спектральная теорема)
существует ОНБ из собственных векторов.
⟹
по Т4.1
(основная спектральная теорема)
существует ОНБ из собственных векторов. - нормальный и
- нормальный и
 ⟹𝒜
– самосопряженный. ∎
⟹𝒜
– самосопряженный. ∎ - эрмитова ⟺ все собственные
значения
матрицы
- эрмитова ⟺ все собственные
значения
матрицы
 вещественны и существует унитарная
матрица
вещественны и существует унитарная
матрица
 ,
столбцы которой – собственные векторы
матрицы
,
столбцы которой – собственные векторы
матрицы
 ,
отвечающие собственным значениям
,
отвечающие собственным значениям
 .
. -
эрмитова матрица ⟺
для любого ОНБ
-
эрмитова матрица ⟺
для любого ОНБ
 - самосопряжен ⟺
- самосопряжен ⟺
 - нормален и
- нормален и
 ⟺
⟺ - нормальная матрица и
- нормальная матрица и
 ⟺
⟺
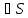 –
унитарная матрица
–
унитарная матрица .
∎
.
∎ - унитарный ⟺ существует ОНБ из
собственных векторов и
- унитарный ⟺ существует ОНБ из
собственных векторов и
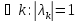 .
. – унитарный ⟹
– унитарный ⟹
 - нормальный и
- нормальный и
 ⟹ существует ОНБ из собственных
векторов.
⟹ существует ОНБ из собственных
векторов.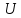 - нормальный и
- нормальный и
 ⟹
⟹
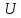 – унитарный. ∎
– унитарный. ∎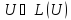 -
унитарный ⟺ существует ОНБ из
собственных векторов и
-
унитарный ⟺ существует ОНБ из
собственных векторов и
 .
. – унитарный ⟹
– унитарный ⟹
 - нормальный и
- нормальный и
 ⟹ существует ОНБ из собственных
векторов.
⟹ существует ОНБ из собственных
векторов.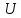 - нормальный и
- нормальный и
 ⟹
⟹
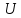 – унитарный. ∎
– унитарный. ∎ - унитарна ⟺ существует унитарная
матрица
- унитарна ⟺ существует унитарная
матрица
 .
.
 -
унитарна ⟺ в любом ОНБ
-
унитарна ⟺ в любом ОНБ
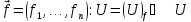 - унитарный оператор ⟺
- унитарный оператор ⟺
 - нормальный и
- нормальный и
 ⟺ существует унитарная матрица
⟺ существует унитарная матрица
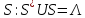 .∎
.∎ называется положительно определенным,
если для
называется положительно определенным,
если для
 и неотрицательно определенным, если
и неотрицательно определенным, если
 .
. задан ОНБ:
задан ОНБ:
 ,
тогда
,
тогда
 - эрмитова квадратичная форма от
переменных
- эрмитова квадратичная форма от
переменных
 ,
причем, если
,
причем, если
 - положительно определен, то
- положительно определен, то
 положительно определена (аналогично
для неотрицательно определенного
оператора
положительно определена (аналогично
для неотрицательно определенного
оператора
 ).
). - самосопряженный оператор является
положительно определенным (неотрицательно
определенным) ⟺
все его собственные значения положительны
(неотрицательны):
- самосопряженный оператор является
положительно определенным (неотрицательно
определенным) ⟺
все его собственные значения положительны
(неотрицательны):
 .
. -
самосопряженный оператор ⟺
существует ОНБ из собственных векторов
и
-
самосопряженный оператор ⟺
существует ОНБ из собственных векторов
и
 .
∎
.
∎ – положительно определенный оператор
(неотрицательно определенный),
существует ОНБ из собственных векторов
– положительно определенный оператор
(неотрицательно определенный),
существует ОНБ из собственных векторов
 и
и
 .
Положим
.
Положим
 и определим линейный оператор
и определим линейный оператор
 ⟹
⟹
 - самосопряженный оператор,
- самосопряженный оператор,
 ,
и
,
и
 положительно определенный (неотрицательно
определенный).
положительно определенный (неотрицательно
определенный). ,
связанный с
,
связанный с
 равенством
равенством
 ,
называется арифметическим корнем из
оператора
,
называется арифметическим корнем из
оператора
 и обозначается
и обозначается
 .
. есть неотрицательно определенный
оператор и, если
есть неотрицательно определенный
оператор и, если
 - невырожденный, то и
- невырожденный, то и
 - невырожденный оператор.
- невырожденный оператор.
 ⟹
⟹
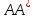 - самосопряженный оператор;
- самосопряженный оператор;
 ⟹
неотрицательно определенный оператор.
⟹
неотрицательно определенный оператор. - невырожденный ⟺
- невырожденный ⟺
 - обратим ⟹
матрица оператора
- обратим ⟹
матрица оператора
 в любом базисе невырожденная ⟹
в любом ОНБ
в любом базисе невырожденная ⟹
в любом ОНБ
 ⟹
⟹
 - невырожденная ⟹
оператор
- невырожденная ⟹
оператор
 невырожденный
⟹
оператор
невырожденный
⟹
оператор
 невырожденный. ∎
невырожденный. ∎ может быть представлен в виде
может быть представлен в виде
 (или
(или
 ),
где
),
где
 - положительно определенный оператор,
- положительно определенный оператор,
 - унитарный оператор.
- унитарный оператор.
 - невырожденный оператор ⟹
- невырожденный оператор ⟹
 невырожденный положительно определенный
оператор. Положим
невырожденный положительно определенный
оператор. Положим
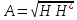 ⟹
⟹
 невырожденный положительно определенный
оператор. Положим
невырожденный положительно определенный
оператор. Положим
 .
Покажем, что
.
Покажем, что
 – унитарный:
– унитарный:
 (
( положительно определенный ⟹
самосопряженный). ∎
положительно определенный ⟹
самосопряженный). ∎ задана эрмитова квадратичная форма
задана эрмитова квадратичная форма
 .
. с матрицей
с матрицей
 при помощи некоторого унитарного
преобразования переменных
при помощи некоторого унитарного
преобразования переменных
 ,
где
,
где
 - унитарная матрица, может быть
приведена к каноническому виду:
- унитарная матрица, может быть
приведена к каноническому виду:
 ,
где
,
где
 и с точностью до порядка определены
матрицей
и с точностью до порядка определены
матрицей
 однозначно (они совпадают с собственными
значениями матрицы
однозначно (они совпадают с собственными
значениями матрицы
 ).
Столбцы унитарной матрицы
).
Столбцы унитарной матрицы
 -
нормированные собственные векторы
матрицы
-
нормированные собственные векторы
матрицы
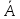 ,
отвечающие собственным значениям
,
отвечающие собственным значениям
 .
. к эрмитовой форме
к эрмитовой форме
 .
.
 определена однозначно (п.9, раздел 2).
Для любой
определена однозначно (п.9, раздел 2).
Для любой
 существует
единственный линейный оператор
существует
единственный линейный оператор
 и в любом ОНБ
и в любом ОНБ
 (п.7,
раздел 3).
(п.7,
раздел 3).
 - эрмитова полуторалинейная форма ⟺
- эрмитова полуторалинейная форма ⟺
 ⟹
⟹ ,
т.е.
,
т.е.
 ⟹
⟹
 -
самосопряженный оператор:
-
самосопряженный оператор:
 .
. .
Согласно спектральной теореме для
самосопряженных операторов (Т6.1)
существует ОНБ из собственных векторов
оператора
.
Согласно спектральной теореме для
самосопряженных операторов (Т6.1)
существует ОНБ из собственных векторов
оператора

 .
. .
.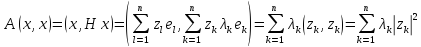 .
. унитарна, как матрица перехода от
одного ОНБ к другому ОНБ. Рассмотрим
матрицу
унитарна, как матрица перехода от
одного ОНБ к другому ОНБ. Рассмотрим
матрицу
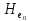 :
:
 .
⟹
.
⟹ . ∎
. ∎ .
. и
и
 эрмитовы квадратич. формы
эрмитовы квадратич. формы
 .
Найдем невырожденное преобразование
координат, одновременно приводящее
эрмитовы квадратич. формы к канонич.
виду.
.
Найдем невырожденное преобразование
координат, одновременно приводящее
эрмитовы квадратич. формы к канонич.
виду. и
и
 эрмитовы квадратичные формы в
комплексном пространстве, причем
эрмитовы квадратичные формы в
комплексном пространстве, причем
 .
Тогда существует базис
.
Тогда существует базис
 ,
в котором
,
в котором
 и
и
 имеют канонич. вид:
имеют канонич. вид:
 где
где
 .
. ,
полярную к эрмитовой квадратич. форме
,
полярную к эрмитовой квадратич. форме
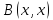 .
В
.
В
 введем скалярное произведение с
помощью
введем скалярное произведение с
помощью
 .
Рассм.
.
Рассм.
 с введенным скалярным произведением
– это унитарное пространство. Тогда
сущ. унитарное преобразование (п.7),
приводящее эрмитову квадратич. форму
к канонич. виду:
с введенным скалярным произведением
– это унитарное пространство. Тогда
сущ. унитарное преобразование (п.7),
приводящее эрмитову квадратич. форму
к канонич. виду:
 .
Т.к.
.
Т.к.
 – унитарная матрица (⟺
матрица перехода от одного ОНБ к
другому ОНБ) ⟹
– унитарная матрица (⟺
матрица перехода от одного ОНБ к
другому ОНБ) ⟹
 - ОНБ и
- ОНБ и
 , где
, где
 .∎
.∎ и
и
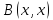 ,
называется совокупность форм
,
называется совокупность форм
 ,
где
,
где
 - параметр. Если
- параметр. Если
 ,
то пучок называется регулярным.
,
то пучок называется регулярным. и
и
 - матрицы
- матрицы
 и
и
 в некотором базисе. Уравнение
в некотором базисе. Уравнение
 называется характеристическим
уравнением пучка
называется характеристическим
уравнением пучка
 .
. - какой-нибудь корень характеристич.
уравнения, то
- какой-нибудь корень характеристич.
уравнения, то
 .
. ,
удовлетв. характеристич.уравнению
пучка, называется собственным значением
пучка,
,
удовлетв. характеристич.уравнению
пучка, называется собственным значением
пучка,
 называется главным вектором пучка.
называется главным вектором пучка. и
и
 - эрмитовы квадратич. формы,
- эрмитовы квадратич. формы,
 .
Тогда существует невырожденное
преобразование:
.
Тогда существует невырожденное
преобразование:
 с матрицей
с матрицей
 ,
где
,
где
 - главные векторы – столбцы пучка
- главные векторы – столбцы пучка
 ,
ормированные в смысле скалярного
произведения
,
ормированные в смысле скалярного
произведения
 (
( - полярная полуторалинейная форма к
эрмитовой форме
- полярная полуторалинейная форма к
эрмитовой форме
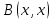 ),
т.е.
),
т.е.
 ,
приводящее эрмитовы квадратич. формы
к канонич.виду:
,
приводящее эрмитовы квадратич. формы
к канонич.виду: ,
,
 - собственные значения пучка
- собственные значения пучка
 ,
соответствующие столбцам матрицы
,
соответствующие столбцам матрицы
 .
. пучка
пучка
 вещественны и им соответствует
вещественны и им соответствует
 линейно независимых главных векторов
линейно независимых главных векторов
 :
:
 ,
которые могут быть выбраны так, что
,
которые могут быть выбраны так, что
 .
. .
Обозначим
.
Обозначим
 Т.к.
Т.к.
 – положительно определенная квадратичная
форма ⟹
матрица
– положительно определенная квадратичная
форма ⟹
матрица
 – положительно определена. Рассмотрим
матрицу
– положительно определена. Рассмотрим
матрицу
 :
: .
.

 ,
, - симметрические матрицы ⟹
- симметрические матрицы ⟹
 - симметрическая ⟹
существует ортогональная матрица,
столбцами которой являются собственные
векторы-столбцы матрицы
- симметрическая ⟹
существует ортогональная матрица,
столбцами которой являются собственные
векторы-столбцы матрицы
 и
и
 .
.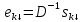 - собственный вектор матрицы
- собственный вектор матрицы
 .
. ,
т.е.
,
т.е.
 – собственный вектор матрицы
– собственный вектор матрицы
 и
и
 .
Векторы
.
Векторы
 могут быть выбраны так, что:
могут быть выбраны так, что:
 .2)
Рассмотрим
.2)
Рассмотрим
 .
Покажем, что
.
Покажем, что
 :
: .∎
.∎