
3 семестр экзамен / Ekzamen_Linal / 3 раздел / 3_1-3_5
.docx|
3.1 Опр. и примеры евклидовых и унитарных пространств. Линейные нормированные пространства. Нер-во Коши-Буняковского. линейные нормированные пространства. Нер-во треугольника. Опр.
1.1
Пусть
1)
3) Число
Примеры:1)
2)
3)
Простейшие св-ва скалярного произведения: 1)
2)
3)
4)
■ 3)
Теорема
1.1
(неравенство
Коши – Буняковского)
Для
Т.к.
Тогда
Опр
1.2
Линейное комплексное прост-во наз-тся
линейным нормированным
простр-вом,
если для
1)
2)
3)
Примеры:
1)
2)
Теорема
2
Всякое унитарное пр-во является
нормиро-ванным, если в нем определить
норму:
■1)
2)
3)
Замечание
1)
Теорема
1.3
Нер-во:
■
|
3.2 Общий вид скалярного произведения в евклидовом и унитарном пространстве. Матрица Грама. Пусть
Обозначим:
Рассмотрим
матрицу
Определение
2.1
Матрица
Запись
Замечание1)
Т.к.
2)
Теорема
2.1
Пусть
■
|
3.3 Ортогональные вектора. Ортонормированный базис (ОНБ). Ортогонализация Шмидта. Опр
3.1
Эл-ты
Замечание
1. Нулевой элемент
Опр
3.2
Система векторов унитарного пространства
наз-ся ортонормированной (ОНС), если
Теорема
3.1
Ортогональная система ненулевых
векторов
Следствие 1. Ортонормированная система векторов линейно независима. Следствие
2. В
Теорема
3.2
В евклидовом (унитарном) пространстве
координаты
∎ «⟹»
Пусть
«⟸»
Пусть
Теорема
3.3
В унитарном пространстве скалярное
произведение векторов
∎ «⟹»
«⟸» В силу линейности скалярного произведения. ∎ Замечание
2.
В евклидовом простр-ве
Теорема
4.1
(Шмидта об ортогонализации) Пусть в
унитарном пространстве
∎ Построение ОНБ методом математической индукции.
Пусть
в унитарном пространстве
Докажем,
что в унитарном пространстве размерности
Положим
Следствие. Во всяком –мерном пространстве существует ОНБ.
|
3.4 Ортогональное дополнение. Теорема о представлении унитарного пространства в виде прямой суммы линейных подпространств. Опр
5.1
Пусть
Опр
5.2
Подпространства
Опр
5.3
Совокупность всех векторов
Теорема
5.1
Ортогональное дополнение
∎
Теорема
5.2
∎ Пусть
Теорема
5.3
Унитарное пространство
∎ Пусть
Обратно:
Т.к.
|
3.5 Линейная форма в линейном пространстве. Сопряженное пространство и его размерность. биортогональный базис. Представление линейной формы в унитарном (евклидовом) пространстве. Теорема
6.1
∎ Пусть
Рассмотрим
Следовательно,
Докажем единственность. Пусть
В
Покажем,
что
∎1)
2) Докажем линейную независимость.
Положим
Опр
6.1
|

 - вещественное или комплексное ЛП.
Отображение
- вещественное или комплексное ЛП.
Отображение
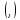
 (
( или
или )
наз-тся скалярным
произведением,
если
)
наз-тся скалярным
произведением,
если

 2)
2)

 4)
4)
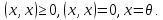
 называется скалярным
произведением;
1) – 4) – аксиомами скалярного
произведения. Вещественное ЛП со
скалярным произведением наз-ся
евклидовым
пространством:
называется скалярным
произведением;
1) – 4) – аксиомами скалярного
произведения. Вещественное ЛП со
скалярным произведением наз-ся
евклидовым
пространством:
 ;
комплексное ЛП со скалярным произведением
наз-ся унитарным
пространством:
;
комплексное ЛП со скалярным произведением
наз-ся унитарным
пространством:
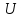 .
.


 ;
; ;
; ;
; .
. .
4) «⟸»
3)«⟹»
.
4) «⟸»
3)«⟹» .
■
.
■
 или
или
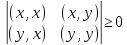 .
■ Пусть
.
■ Пусть
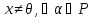 :
: .
. ,
пусть
,
пусть
 .
. .
■
.
■ ставится в соответствие веществ. число
ставится в соответствие веществ. число
 ,
назыв.нормой
указанного элемента, при этом норма
удовлетворяет следующим аксиомам:
,
назыв.нормой
указанного элемента, при этом норма
удовлетворяет следующим аксиомам:

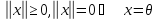 ;
; - однородность нормы;
- однородность нормы; –
неравенство треугольника.
–
неравенство треугольника. - длина
- длина
 .
.
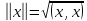 .
. (аксиома 4),
(аксиома 4), ,
,

 (неравенство
Коши Буняковского)
(неравенство
Коши Буняковского)
 .
■
.
■ (неравенство Коши – Буняковского).2)
Введем функцию
(неравенство Коши – Буняковского).2)
Введем функцию
 – расстояние между
– расстояние между
 и
и
 :
1)
:
1)
 ,
2)
,
2)
 ,
3)
,
3)
 .
. .
. ;
;

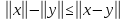 ,
, .
■
.
■ – базис в
– базис в
 .
. ,
, .
.
 .
.
 .
. называется матрицей
Грама
системы векторов
называется матрицей
Грама
системы векторов
 :
: .
. называется общим
видом
скалярного произведения в унитарном
пространстве.
называется общим
видом
скалярного произведения в унитарном
пространстве. – эрмитова матрица.
– эрмитова матрица. - евклидово пространство:
- евклидово пространство:
 - симметричная матрица и
- симметричная матрица и
 - общий вид скалярного произведения
в евклидовом пространстве.
- общий вид скалярного произведения
в евклидовом пространстве. и
и
 базисы в
базисы в
 .
Тогда
.
Тогда
 .
. .
■
.
■ наз-тся ортогональными
наз-тся ортогональными
 ,
если их скалярное произведение равно
нулю:
,
если их скалярное произведение равно
нулю:
 .
. ,
и только нулевой, ортогонален любому
вектору пространства.
,
и только нулевой, ортогонален любому
вектору пространства. (символ Кронекера).
(символ Кронекера). - линейно независима. ∎
Пусть
- линейно независима. ∎
Пусть
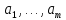 ортогональная система. Достаточно
д-ть, что равенство
ортогональная система. Достаточно
д-ть, что равенство
 достигается только при
достигается только при
 .
Умножим скалярно на
.
Умножим скалярно на
 ,
т.к.
,
т.к.
 .∎
.∎ - мерном пространстве любая ОНС из
- мерном пространстве любая ОНС из
 векторов образует базис.
векторов образует базис. вектора
вектора
 в базисе
в базисе
 вычисляются по правилу
вычисляются по правилу
 тогда и только тогда, когда
тогда и только тогда, когда
 - ортонормированный базис.
- ортонормированный базис. .
Тогда
.
Тогда
 - тоже вычисляются по этому же правилу.
Следовательно,
- тоже вычисляются по этому же правилу.
Следовательно,
 .
. - ОНБ, следовательно, из линейности
скалярного произведения ⟹
- ОНБ, следовательно, из линейности
скалярного произведения ⟹
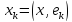 .∎
.∎
 и
и
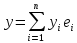 вычисляется по правилу
вычисляется по правилу
 тогда и только тогда, когда
тогда и только тогда, когда
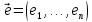 - ОНБ.
- ОНБ. .
. .
. задан произвольный базис
задан произвольный базис
 .
Тогда в
.
Тогда в
 существует ОНБ
существует ОНБ
 ,
который можно построить следующим
образом:
,
который можно построить следующим
образом:
 ,
где
,
где
 .
. ,
т.к. система линейно независима.
,
т.к. система линейно независима. ,
размерности
,
размерности
 ,
существует ОНБ
,
существует ОНБ
 и
и
 ,
,
 .
. существует ОНБ. Пусть
существует ОНБ. Пусть
 - произвольный базис
- произвольный базис
 .
.
 – линейная оболочка
– линейная оболочка
 - есть унитарное –мерное пространство.
Следовательно, по предположению
индукции в нем существует ОНБ
- есть унитарное –мерное пространство.
Следовательно, по предположению
индукции в нем существует ОНБ
 ,
удовлетворяющий условиям теоремы.
Рассмотрим вектор
,
удовлетворяющий условиям теоремы.
Рассмотрим вектор
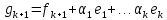 - линейная комбинация
- линейная комбинация
 .
Т.к.
.
Т.к.
 линейно независимы, ⟹,
линейно независимы, ⟹,
 .
Числа
.
Числа
 подберем так, чтобы
подберем так, чтобы
 .
Умножим
.
Умножим
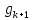 на
на
 :
:
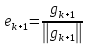 .
Следовательно,
.
Следовательно,
 образуют базис в
образуют базис в
 .∎
.∎ – линейное подпространство унитарного
(евклидова) пространства:
– линейное подпространство унитарного
(евклидова) пространства:
 .
Вектор
.
Вектор
 наз-ся ортогональным к подпространству
наз-ся ортогональным к подпространству
 ,
если он ортогонален
,
если он ортогонален
 :
: .
. .
. и
и
 наз-ся ортогональными
наз-ся ортогональными
 .
. ,
ортогональных подпространству
,
ортогональных подпространству
 ,
наз-ся ортогональным дополнением к
,
наз-ся ортогональным дополнением к
 до пространства
до пространства
 и обозначается
и обозначается
 :
: .
. является линейным подпространством.
является линейным подпространством. .
∎
.
∎ .
.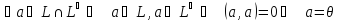 .
∎
.
∎ есть прямая сумма любого своего
подпространства
есть прямая сумма любого своего
подпространства
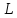 и его ортогонального дополнения
и его ортогонального дополнения
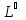 ,т.е.
,т.е.
 .
.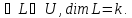 Если
Если
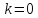 ⟹
⟹
 - тривиальное подпространство.
- тривиальное подпространство.
 – ОНБ в
– ОНБ в
 .
Дополним его до базиса
.
Дополним его до базиса
 (по теореме о неполном базисе):
(по теореме о неполном базисе):
 . Ортонормируем систем (теорема Шмидта)
⟹
получим ОНБ в
. Ортонормируем систем (теорема Шмидта)
⟹
получим ОНБ в
 .
Покажем, что
.
Покажем, что

 .
. ,
т.к.
,
т.к.
 – ОНБ в
– ОНБ в
 ⟹
⟹
 .
.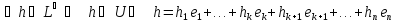 ,
где
,
где
 .
. .
∎
.
∎ - унитарное пространство. Для любой
линейной формы
- унитарное пространство. Для любой
линейной формы
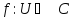 в унитарном пространстве
в унитарном пространстве
 существует, и притом единственный,
вектор
существует, и притом единственный,
вектор
 такой, что
такой, что
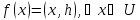 .
. - ОНБ в
- ОНБ в
 ,
,
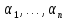 - коэффициенты линейной формы в базисе
- коэффициенты линейной формы в базисе
 ,
т.е.
,
т.е.
 .
. .
. ,
тогда
,
тогда .
. - удовлетворяет условию
- удовлетворяет условию
 .
. .
∎
.
∎
 -
пространство, сопряженное к
-
пространство, сопряженное к
 .
. определим функционалы
определим функционалы
 .
Их достаточно определить на базисных
векторах:
.
Их достаточно определить на базисных
векторах:

 .
. образуют базис в
образуют базис в
 .
.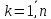 ⟹ их
⟹ их
 .
. -
нулевой функционал:
-
нулевой функционал:
 .
.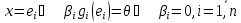 ⟹
линейно независимы ⟹
образуют базис.∎
⟹
линейно независимы ⟹
образуют базис.∎ наз-ся биортогональным базисом к
базису
наз-ся биортогональным базисом к
базису
 .
.