Министерство образования и науки Российской Федерации

Южно-Уральский государственный университет

Приборостроительный факультет

/компьютерных технологий, управления и радиоэлектроники/

Кафедра «Системы управления»

ОТЧЕТ

по лабораторной работе №1

«ЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ ПЕРВОГО ПОРЯДКА»

Составил:

Студент гр. ПС-316

Ершов В. С. ______

«__» ________ 2012 г.

Проверил:

Зырянов Г. В. ______

« » _______ 2012 г.

Челябинск 2012

Лабораторная работа №1 линейные динамические звенья первого порядка Вариант №1

Цель работы: Изучение и экспериментальное исследование свойств и характеристик ЛДЗ первого порядка во временной и в частотной области.

Параметры из таблицы вариантов:

K₀ = 1.1, T₀ = 0.16

1 Идеальное интегрирующее звено

W(p) = ; h(t)= Kt*1(t); Значения параметров: K = 1.1, 2.2

h(0) = W() = 0; h() = W (0) = ;

1. Исследование переходной функции h(t)

Входной сигнал u(t)=U_вх1(t), где U_вх= 1В.

Таблица 1.1 – Экспериментальные точки для h_э(t)

К = 1.1	t, с	0	0.5
	h(t), В	0	0.55
К = 2.2	t, с	0	0.5
	h(t), В	0	1.1

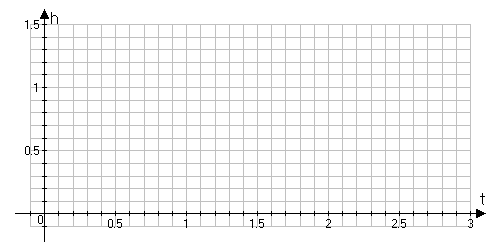
Рисунок 1.1 – Переходные функции:

1 – К = 1.1; 2 – К = 2.2

Выводы: Из графиков видно, что переходный процесс отсутствует. При увеличении K увеличивается угол наклона прямой.

1.2 Исследование частотных характеристик

Входной сигнал u(t) = A_вхsin (_kt) 1(t), где A_вх = 1

_k = 2f_k; M_k = А_вых/А_вх; L_k = 20lg M_k;  = -360*; (Знак минус так как выход запаздывает относительно входа (рисунок1.2)).

Рисунок 1.2 - Схематическое изображение реакции звена на гармоническое входное воздействие

Таблица 1.2 – Экспериментальные точки для ЧХ

K	fk, Гц	k, с–1	lg k	Авых, В	Mk	Lk, дБ		, град
K = 1.1	0.01	0.0628	-1.2	17.5	17.5	24.861	0.25	-90
	0.05	0.314	-0.503	3.32	3.32	10.422	0.25	-90
	*0.18	1.13	0.053	1	1	0	0.25	-90
	0.54	3.391	0.531	0.32	0.32	-9.897	0.25	-90
	1000	6280	75.959	0	0	-	0.25	-90
K = 2.2	0.01	0.0628	-1.2	35	35	30.881	0.25	-90
	0.105	0.659	-0.181	3.27	3.27	10.291	0.25	-90
	*0.35	2.198	0.342	1	1	0	0.25	-90
	1.05	6.594	0.819	0.33	0.33	-9.629	0.25	-90
	1000	6280	75.959	0	0	-	0.25	-90

Данные для построения теоретических (асимптотических) ЛЧХ:

20lg K₁=0.828;

20lg K₂=6.848;

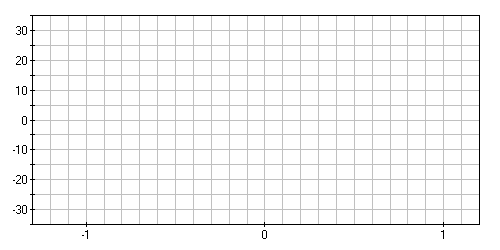
Рисунок 1.3 – Графики ЛАХ и ЛФХ:

1 - ЛАХ: К = 1.1;

2 - ЛФХ: К = 1.1;

3 - ЛАХ: К = 2.2;

4 - ЛФХ: К = 2.2

Выводы: параметр K является коэффициентом усиления, также является тангенсом угла наклона графика переходной функции. Его увеличение приводит к пропорциональному увеличению выходного сигнала. На графике ЛАХ увеличение K приводит к плоскопараллельному сдвигу кривой ЛАХ вверх. Нулю графика ЛАХ соответствует значение частоты среза _ср, равное параметру K. ЛФХ не зависит от параметра K.