3.3.Статический расчет обделки.

Расчет выполнен с помощью проектно-вычислительного комплекса SCAD.

В основу расчета положен метод конечных элементов с использованием в качестве основных неизвестных перемещений и поворотов узлов расчетной схемы. В связи с этим идеализация конструкции выполнена в форме, приспособленной к использованию этого метода, а именно: система представлена в виде набора тел стандартного типа (стержней, пластин, оболочек и т.д.), называемых конечными элементами и присоединенных к узлам.

Тип конечного элемента определяется его геометрической формой, правилами, определяющими зависимость между перемещениями узлов конечного элемента и узлов системы, физическим законом, определяющим зависимость между внутренними усилиями и внутренними перемещениями, и набором параметров (жесткостей), входящих в описание этого закона и др.

Для расчета используем данные из таблицы 3.3.1:

Рисунок 3.3.1. Расчетная жесткость сечения.

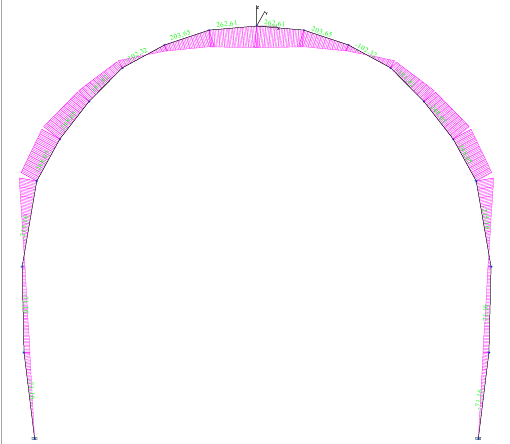
Рисунок 3.3.2. Эпюра момента.

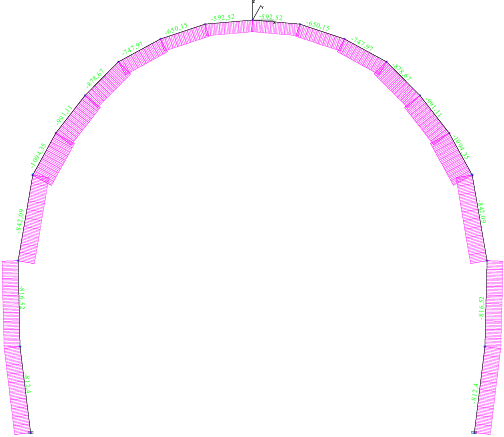
Рисунок 3.3.2. Эпюра продольныхсил.

Таблица 3.3.1. Расчетные данные.

№	αn	Д	Дх	Ду	Q0	P	H
1					208	1	0,7
2					203	2	0,704
3					193	5	0,717
4					171	7	0,737
5					146	9	0,764
6					126	10	0,797
7	70,75	357173	337204	117755	107	17	0,828
8	85,85	460886	459680	33319,6	75	22	0,887
9	94,18	460886	459663	-33554,4	52	22	1,049
10		438122			69	11	1,4

Прочность принятой монолитной обделки проверяется в соответствии со СНиП 2.03.01-84. В соответствии с этими нормами напряжения от действующих усилий не должны превышать расчетных сопротивлений бетона: R_b и R_bt.

Для расчета принимаем сечения обделки с наибольшим положительным моментом М и соответствующей нормальной силой N. Сперва, определяем расчетный эксцентриситет приложения силы:

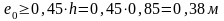
Вычислим расчетную длину элемента для определения гибкости данного элемента:

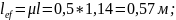
μ – коэффициент приведения длины, принимается в зависимости от вида обделки;

l – длина элемента вдоль его геометрической оси;

Вычислим гибкость элемента, для выяснения учитываемости коэффициента η

где h – высота расчетного сечения

т.к. λ< 4, то коэффициент η исключается из формулы расчета прочности сечения

Проверяем условие:

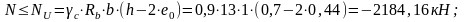
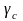–коэффициент условий работы,

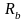– расчетное сопротивление бетона осевому сжатию(для В25R_b=13 МПа);

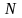– нормальная сила в сечении обделки.

Значит, предельное состояние обуславливается расчетным сопротивлением бетона растяжению (случай, не допускающий появление трещин):

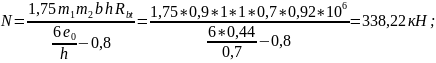
где m₁ – коэффициент, учитывающий возможную неточность при принятии расчетной схемы обделки (m₁ = 0,9);

m₂ – коэффициент, учитывающий понижение прочности бетона при отсутствии наружной гидроизоляции (m₂ = 1);

1,75 – коэффициент повышения несущей способности за счет проявления пластических деформаций;

R_bt – расчетное сопротивление бетона осевому растяжению (для В25R_bt=0,92 МПа);

b, h – ширина и высота расчетного сечения, м.

Условие не соблюдается, т.к. 338,22 кН<592,52 кН

Увеличиваем толщину обделки, и класс бетона (В35, R_b=17,5 Мпа,R_bt=1,15 МПа) и проверяем прочность нового сечения:

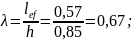
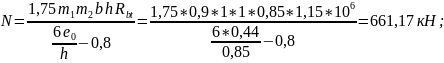
Условие соблюдается, т.к. 661,17 кН>592,52кН.

Прочность обделки обеспечена.