
- •1. Варианты заданий Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •Задание № 6
- •Задание № 7
- •Задание № 8
- •Задание № 9
- •Задание № 10
- •Задание № 11
- •Задание № 12
- •Задание № 13
- •Задание № 14
- •Задание № 15
- •Задание № 16
- •Задание № 17
- •Задание № 18
- •Задание № 19
- •Задание № 20
- •Задание № 21
- •Задание № 22
- •Задание № 23
- •Задание № 24
- •Задание № 25
- •Задание № 26
- •Задание № 27
- •Задание № 28
- •Задание № 29
- •Задание № 30
- •2.3. Блок-схема алгоритма
- •2.4. Тестовый пример решения системы двух уравнений
- •2.5. Выполнение задания на компьютере
- •3. Фонд заданий
- •3.1. Нелинейные уравнения
- •3.2. Системы двух нелинейных уравнений
- •3.3. Системы линейных уравнений
- •4.4. Интерполяция и аппроксимация
- •3.5. Определенные интегралы
- •3.6. Кратные интегралы
- •Библиографический список
- •Приложение Примеры выполнения заданий с использованием excel и vba
2.3. Блок-схема алгоритма
Блок схема алгоритма метода Ньютона приведена на рис. 1.
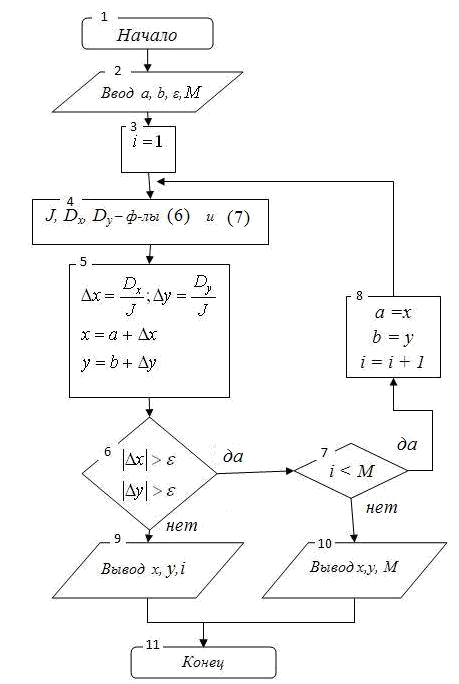
Рис. 1. Блок-схема алгоритма метода Ньютона
В
блоке 2 (рис. 1) осуществляется ввод
исходных данных: а,
b
- начальные приближения неизвестных;
![]() - погрешность
вычислений;
- погрешность
вычислений;
![]() -
максимально
-
максимально
допустимое число итераций. В блоке 6 «да» будет в том случае, если выполнятся оба условия. В блоке 5 а, b - значения неизвестных на предыдущей итерации; x, y - значения на рассматриваемой итерации.
2.4. Тестовый пример решения системы двух уравнений
Получим
формулы для
![]() по исходной системе уравнений (см. п.
3.1):
по исходной системе уравнений (см. п.
3.1):
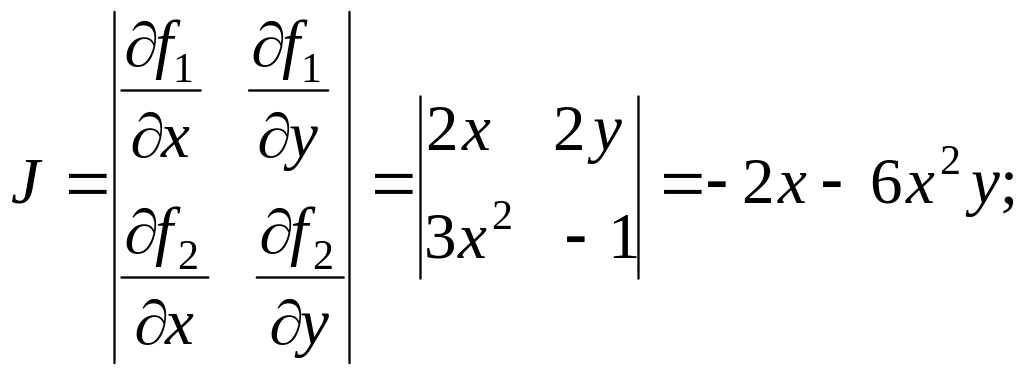
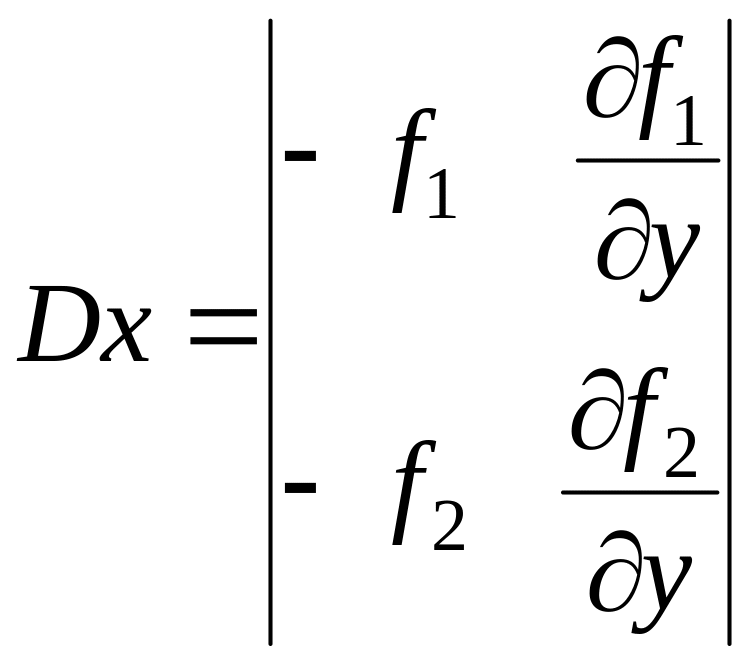 =
=![]()

Итерация i=1: a=0,8; b=0,5; вычислим J, Dх, Dу при x = a; y = b;
J= -3,5200; Dх = -0,0970; Dу = -0,2304;
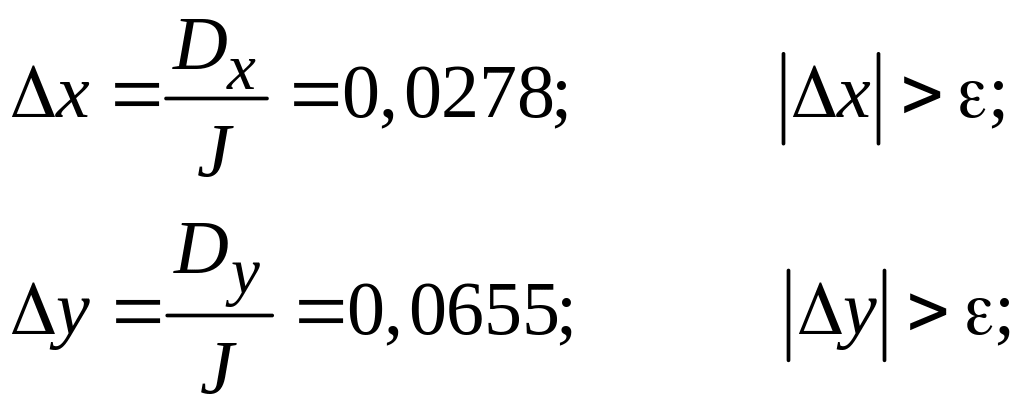
![]()
![]()
Итерация i=2: a = 0,8278; b = 0,5655; вычислим J, Dх, Dу при x = a; y = b;
J = -3,9808; Dх = 0,0072; Dу = 0,0073;
![]()
![]() ;
;
![]() ;
;
![]() ;
;
х = 0,8260; у = 0,5632.
Итерация i=3: a = 0,8260; b = 0,5632; вычислим J, Dх, Dу при x = a; y = b;
J = -3,9596; Dх = 0,0001; Dу = -0,0001;
![]()
![]()
![]()
![]() ;
;
х = 0,8260; у = 0,5636.
Вычисления окончены. Корни заданной системы уравнений с заданной точностью найдены.
2.5. Выполнение задания на компьютере
На рис. 2 представлен лист Excel с исходными данными, результатами табулирования функций, входящих в систему уравнений, графиками функций и результатами расчета. Координаты точки пересечения графиков функций дают приближенное решение системы, т.е. начальные приближения корней a и b.
При табулировании функций формулы для расчета у имеют следующий вид (получены соответственно из первого и второго уравнения):
![]() ,
,
![]() .
.
На рис. 3 представлен лист Excel с копией программы на VBA.
3. Фонд заданий
3.1. Нелинейные уравнения
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
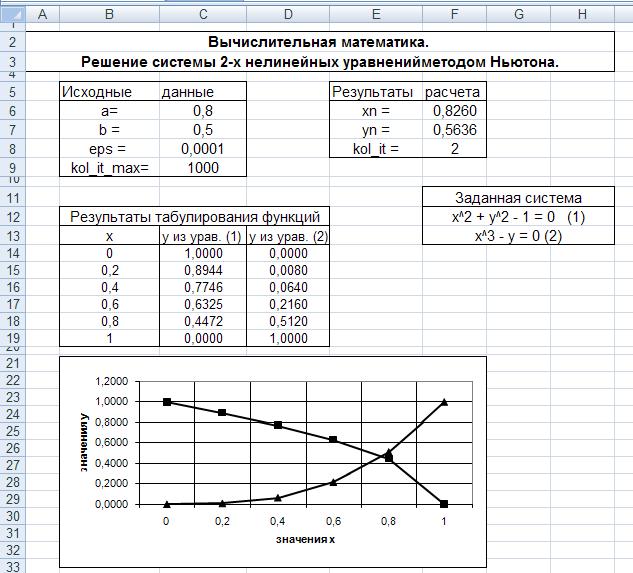

Рис. 2. Лист Excel с исходными данными и результатами
расчета
Рис. 3. Лист Excel с копией программы на VBA
17)
![]() ;
18)
;
18)
![]() ;
;
19)
![]() ;
20)
;
20)
![]() ;
;
21)
![]() ;
22)
;
22)
![]() ;
;
23)
![]() ;
24)
;
24)
![]() ;
;
25)
![]() ;
26)
;
26)
![]() ;
;
27)
![]() ;
28)
;
28)
![]() ;
;
29)
![]() ;
30)
;
30)
![]() .
.
3.2. Системы двух нелинейных уравнений
1
)
 ; 2)
; 2)
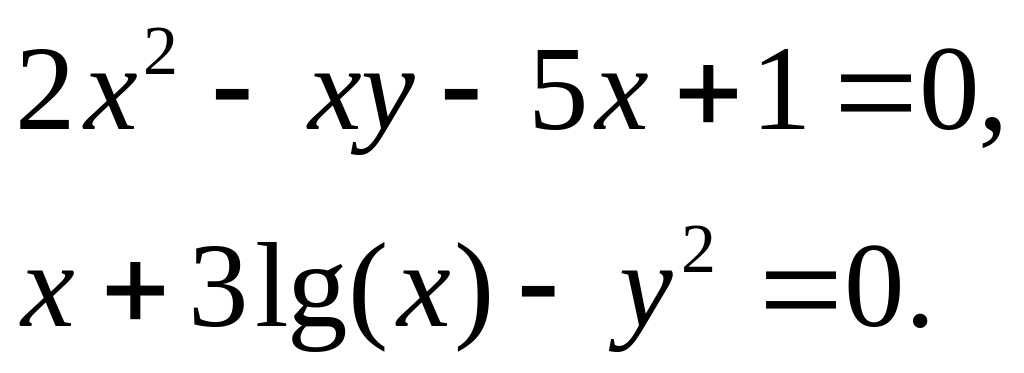 ;
;
3
)
 ; 4)
; 4)
 ;
;
5
)
 ; 6)
; 6)
 ;
;
7
)
![]() ; 8)
; 8)
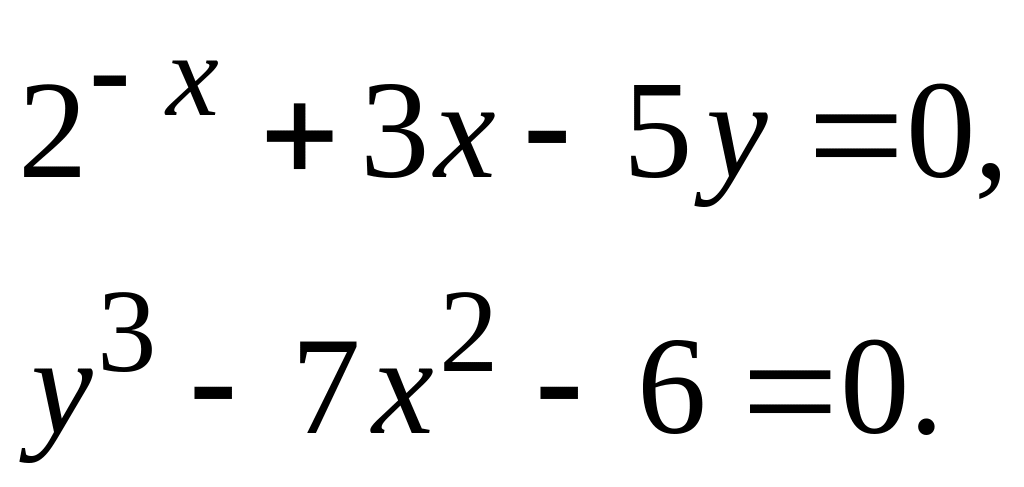 ;
;
9
)
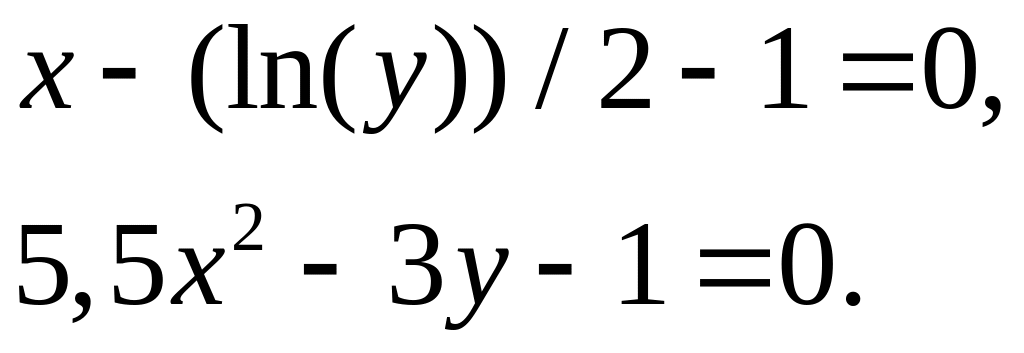 ; 10)
; 10)
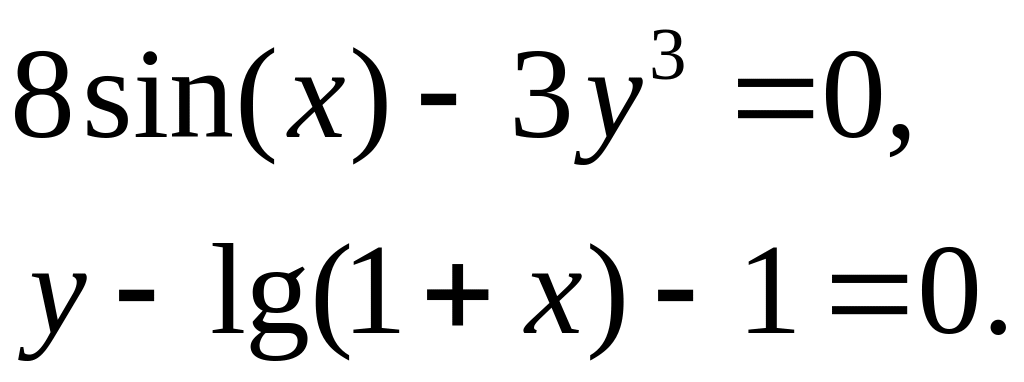 .
.
