Задание № 27

В результате проведения опытов и фиксирования результатов получили

таблицу значений функции (табл. 7). Методом наименьших квадратов определить коэффициенты , и в эмпирических формулах и . Для этого разработать программу на VBA.

Для приведения второго уравнения к линейному виду прологарифмировать его. Привести расчетные значения по обоим уравнениям. Выбрать лучшее уравнение по среднеквадратическому отклонению S. При определении S для второй формулы использовать натуральные (не линеаризованные) расчетные значения у.

Таблица 7

	0,75	1,10	1,50	2,25	3,00	3,50	3,75
	2,50	1,90	1,20	1,12	2,25	3,40	4,53
	0	1	2	3	4	5	6

Наибольшее возможное число опытных точек в программе . Программа должна быть универсальной, т.е. работать при других значениях и

Задание № 28

Составить программу на VBA для вычисления интеграла методом прямоугольников и трапеций с заданной точностью Первоначально отрезок интегрирования разбить на 5 равных частей. Программа должна быть универсальной, т.е работать при замене подынтегральной функции на другую. На печать вывести и число разбиений в конце вычислений. Привести «ручной» расчет методом прямоугольников при первоначальном разбиении отрезка.

Задание № 29

Составить программу на VBA для вычисления кратного интеграла методом ячеек с заданной точностью Первоначально отрезки интегрирования разбить на 4 равные части. Программа должна быть универсальной, т.е. работать при замене подынтегральной функции на другую. На печать вывести и число разбиений в конце вычислений. Привести «ручной» расчет при первоначальном разбиении отрезков.

Задание № 30

Написать программу на VBA для вычисления корней системы из двух нелинейных уравнений

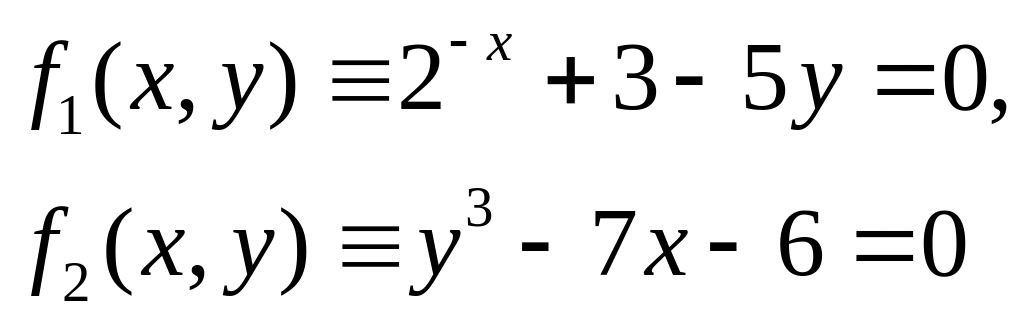
методом Ньютона. Корни определить с пятью значащими цифрами. Предусмотреть счетчик числа итераций и ограничение числа итераций (N = 1000). Напечатать корни и число итераций в конце вычислений. Расчеты выполнить с погрешностью и .

Для и выполнить расчеты с двумя разными начальными приближениями и , т.е. выполнить 4 варианта расчета. Начальные приближения определить графически в Excel с точностью 0,1. Графики привести. Выполнить «вручную» 3 итерации (для одного варианта и начальных приближений).

Задание № 31

Разработать программу на VBA для решения уравнения

методом хорд и уравнения

методом половинного деления. Найти один корень для каждого из уравнений с погрешностью и . Напечатать все исходные данные и результаты расчетов (включая число итераций). Для определения начального отрезка [a,b] протабулировать функции f(x) и привести графики, построенные в Excel.

2. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

2.1. Задание

Вычислить на ПК корни системы из двух нелинейных уравнений

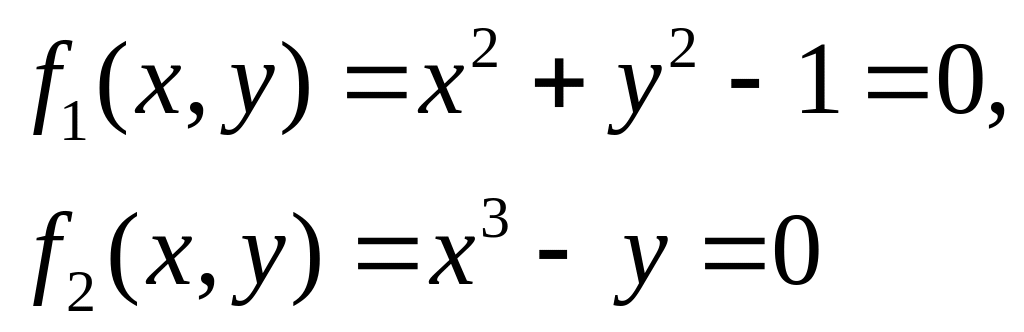
методом Ньютона. Корни определить с пятью значимыми цифрами. Привести число итераций.

Погрешность вычислений равна . Значения начальных приближений и определить графически. Графики привести. Выполнить «вручную» 3 итерации.

2.2. Методика решения системы двух нелинейных уравнений

методом Ньютона

Данный метод обладает гораздо более быстрой сходимостью, чем метод простой итерации. Нужно решить систему двух нелинейных уравнений:

(1)

В основе метода Ньютона для системы уравнений (1) служит разложение функций и в ряд Тейлора, причем члены ряда, содержащие вторые производные и производные более высоких порядков, отбрасываются.

Пусть приближенные значения неизвестных системы (1) равны соответственно и . Их определили из начального приближения или получили на предыдущей итерации. Обозначим приращение (или поправки) к этим значениям и . Через , и решение системы (1) запишется в виде:

. (2)

Проведем разложение левых частей уравнений (1) с учетом (2) в ряд Тейлора, ограничиваясь лишь линейными членами относительно приращений (или производными первого порядка):

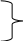(3)

Поскольку в соответствии с (1) левые части этих выражений равны 0, то приравниваем 0 и левые части. Получим следующую систему линейных уравнений относительно приращений

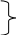(4)

Здесь и далее значения и их производные вычисляются при х = а; у = b.

Неизвестные вычисляются по правилу Крамера:

. (5)

Здесь J – определитель (якобиан) системы (4):

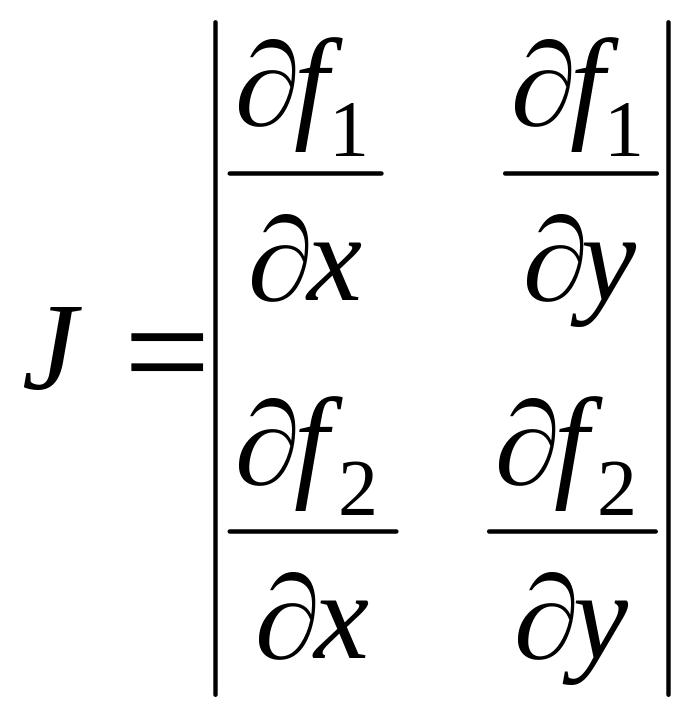. (6)

Для существования единственного решения системы (4) на каждой итерации должно выполнятся условие J ≠ 0.

Определители:

(7)

После определения и по формуле (5), и определяются по формуле (2). Напомним, что здесь а и b - значения неизвестных на предыдущей итерации, а x и y – значения неизвестных на рассматриваемой итерации.

Таким образом, итерационный процесс решения системы (1) методом Ньютона состоит в определении приращений и к значениям неизвестных на каждой итерации. Вычисления прекращаются, если все вычисления становятся малыми по абсолютной величине:

; , (8)

где - заданная точность.

Метод Ньютона применим для решения системы из n уравнений (n = 2, 3, 4, …). Следует учитывать, что сходимость итерационного процесса ухудшается с увеличением n. Для обеспечения хорошей сходимости важен выбор первого приближения.