Задание № 18

Написать программу на VBA для вычисления корней системы из двух нелинейных уравнений

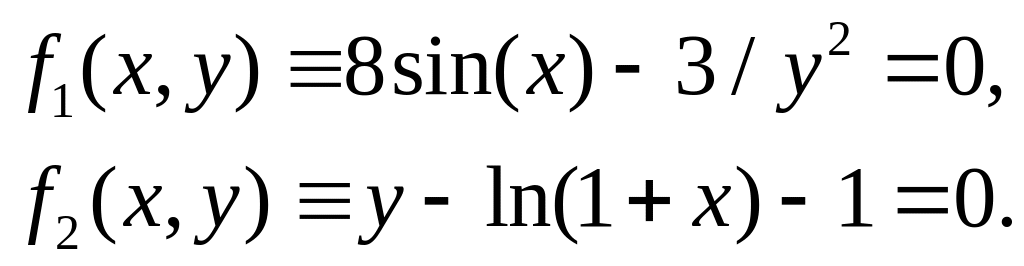
методом Ньютона. Корни определить с пятью значащими цифрами. Предусмотреть счетчик числа итераций и ограничение числа итераций (N = 1000). Печатать корни и число итераций. Расчеты выполнить с погрешностью и .

Для и выполнить расчеты с двумя разными начальными приближениями и , т.е. выполнить 4 варианта расчета. Начальные приближения определить графически в Excel с точностью 0,1. Графики привести. Выполнить «вручную» 3 итерации (для одного варианта начальных приближений).

Задание № 19

Разработать программу на VBA для решения уравнения

методами половинного деления и хорд. Найти хотя бы один корень уравнения. Погрешности решения и . Печатать все исходные данные и результаты расчетов: погрешность, границы отрезка, число итераций в конце вычислений. Для определения начального отрезка [a,b] протабулировать функцию f(x) и привести график, построенный в Excel. Выполнить «вручную» по 5 итераций для каждого метода.

Задание № 20

Разработать программу на VBA для решения уравнения

методом половинного деления и простых итераций. Найти один корень. Погрешности решения и . Напечатать все исходные данные и результаты расчетов (включая число итераций и ограничение числа итераций для второго метода). Выполнить «вручную» по 5 итераций для каждого метода. Для определения начального отрезка [a,b] или начального приближения х₀ протабулировать функцию f(x) и привести график, построенный в Excel.

Задание № 21

Разработать программу на VBA для решения уравнения

методом хорд и простых итераций. Найти корень уравнения с погрешностью и . Напечатать все исходные данные и результаты расчетов (включая число итераций и ограничение этого числа для второго метода). Для определения начального отрезка [a,b] или начального приближения х₀ протабулировать функцию f(x) и привести график, построенный в Excel. Выполнить «вручную» по 5 итераций для каждого метода.

Задание № 22

Разработать программу на VBA для решения системы из трех линейных уравнений методами Гаусса и Зейделя. Программу написать так, чтобы коэффициенты при неизвестных и свободные члены можно было изменять при вводе исходных данных. Программу использовать для решения системы:

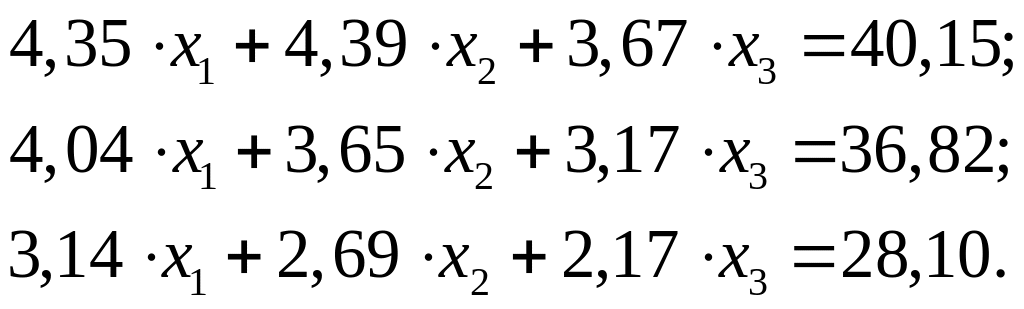
Привести решение методом Гаусса «вручную» с пятью значащими цифрами после запятой.

Корни печатать с пятью знаками после запятой. Напечатать также начальные приближения, заданную погрешность ( ), число итераций, заданное ограничение числа итераций. Корни, вычисленные методом Гаусса, использовать в качестве начальных приближений в методе Зейделя (приближения задавать с точностью до целых). Методом Зейделя «вручную» выполнить 4 итерации.

Задание № 23

Разработать программу на VBA для решения системы из 5 уравнений методом Гаусса. Программу написать так, чтобы коэффициенты при неизвестных и свободные члены можно было изменять при вводе исходных данных. Решить систему:

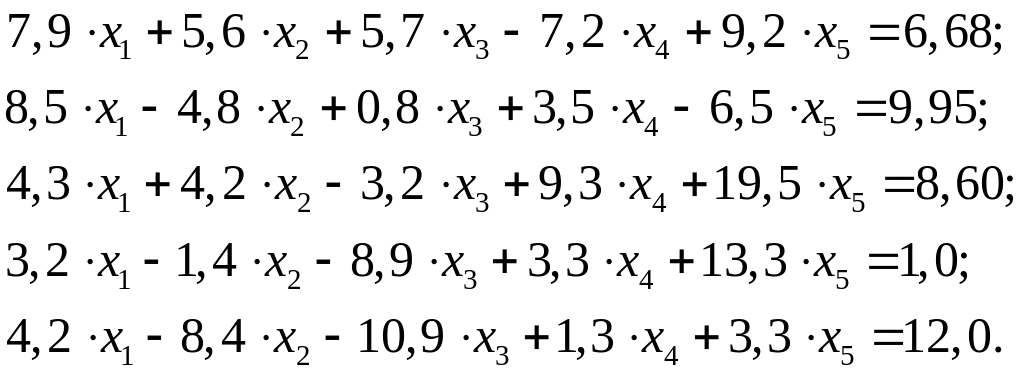
Корни печатать с пятью цифрами после запятой. Напечатать все исходные данные. Привести решение системы «вручную» с пятью значащими цифрами после запятой. Решить эту же систему методом Крамера в Excel, используя для вычисления определителей функцию МОПРЕД.