УДК 519.6(07)
З-813
Золотухин, П.И. Вычислительная математика: методическая разработка к проведению практических занятий и выполнению заданий / П.И. Золотухин – Липецк: Издательство МИКТ ЛФ, 2012. – 29 с.
Методическая разработка предназначена для студентов специальности «Вычислительные машины, сети и комплексы».
В работе приведены индивидуальные варианты заданий и рекомендации, необходимые для их выполнения на компьютере. Варианты заданий охватывают следующие темы: интерполяция; численное интегрирование; решение систем линейных уравнений; определение корней алгебраических и трансцендентных уравнений; решение систем нелинейных уравнений; определение коэффициентов эмпирических формул (метод наименьших квадратов).
Табл. 7. Ил. 3. Библиогр.: 20 назв.
© Золотухин П.И., 2012
© МИКТ ЛФ, 2012
1. Варианты заданий Задание № 1
Написать программу на VBA для вычисления корней системы из двух нелинейных уравнений
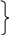
методом
простой итерации. Корни определить
(вывести на печать) с пятью значащими
цифрами. Предусмотреть счетчик итераций.
Напечатать корни и число итераций.
Предусмотреть ограничение числа итераций
(например, 1000). Погрешность вычислений
равна
и
.
Расчеты при каждом значении
выполнить с двумя разными начальными
приближениями
и
,
т.е. выполнить 4 варианта расчета.
Начальные приближения определить
графически с точностью 0,1. Привести
графики, построенные в Excel.
Выполнить «вручную» 5 итераций (для
одного варианта
и одного начального приближения).
Задание № 2
Написать программу на VBA для вычисления корней системы из двух нелинейных уравнений
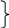
методом
Ньютона. Корни определить с пятью
значащими цифрами. Предусмотреть счетчик
числа итераций и ограничение числа
итераций (N
= 1000). Печатать корни и число итераций в
конце вычислений. Расчеты выполнить с
точностью
и
.
Для точности
выполнить расчет с двумя разными
начальными приближениями
и
.
Аналогично выполнить расчет для
,
т.е. выполнить 4 варианта расчета. Привести
графики для определения
и
(с точностью 0,1), построенные в Excel.
Выполнить «вручную» 3 итерации (для
одного варианта
и одного начального приближения).
Задание № 3
Написать программу на VBA для вычисления корней системы из трех
нелинейных уравнений
,
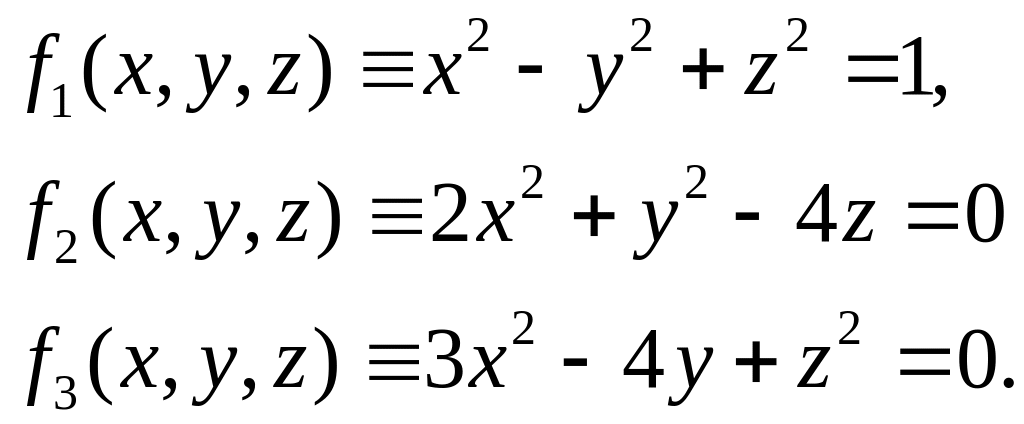
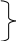методом Ньютона. Корни определить с 5 значащими цифрами. Предусмотреть ограничение числа итераций (N = 500). Напечатать корни, число итераций, начальные приближения, N, точность. Расчеты выполнить с двумя погрешностями и . Для каждой погрешности задать по 2 разных начальных приближения ( и ). Выполнить «вручную» 2 итерации (для одного варианта и одного начального приближения).
Задание № 4
Написать программу на VBA для решения системы нелинейных уравнений
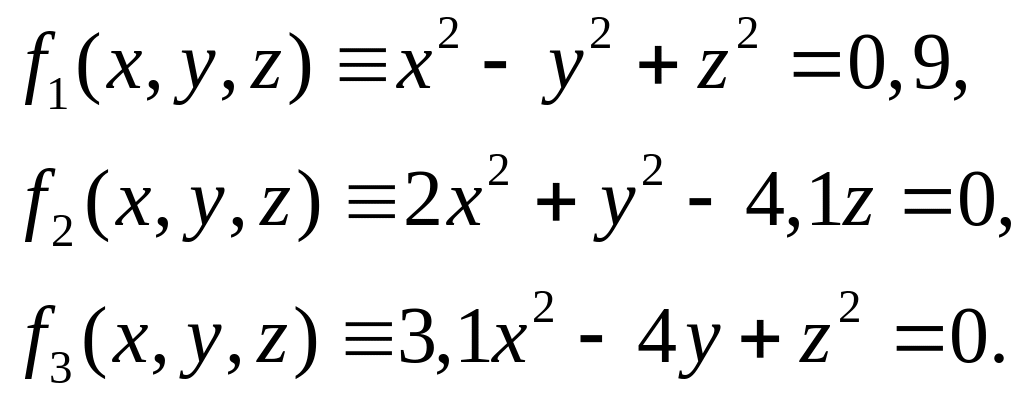
методом
Зейделя. Корни определить с 5 значащими
цифрами. Напечатать все исходные данные
и результаты расчетов: начальные
приближения, корни, число итераций,
заданные погрешность и максимальное
число итераций. Погрешность
.
Задать по два варианта начальных
приближения. Если система не решается
методом Зейделя, решить методом Ньютона.
Задание № 5
Разработать
программу на VBA
для решения уравнения
методом половинного деления и методом хорд. Найти хотя бы один корень уравнения. Погрешности решения и . Напечатать все исходные данные и результаты расчетов: погрешность, границы отрезка, число итераций.
Для определения начального отрезка [a,b] протабулировать функцию f(x) и привести график, построенный в Excel. Выполнить «вручную» по 5 итераций для каждого метода.
Задание № 6
Разработать
программу для решения на VBA
уравнения
методом
половинного деления и простых итераций.
Найти все корни на отрезке
.
Погрешности решения
и
.
Напечатать все исходные данные и
результаты расчетов (включая число
итераций и ограничение числа итераций).
Выполнить «вручную» по 5 итераций для каждого метода. Для определения начального отрезка [a,b] или начального приближения х0 протабулировать функцию f(x) и привести график, построенный в Excel.