13. Изображение взаимно перпендикулярных плоскостей, прямых и плоскостей.

Плоскости:

Две плоскости взаимно перпендикулярны:

- если одна из них проходит через перпендикуляр к другой плоскости (рис. 5.6);

- если одна из плоскостей проходит перпендикулярно прямой, рас-

положенной в другой плоскости .

Иными словами, две плоскости взаимно перпендикулярны, если

имеется возможность провести прямую, принадлежащую одной плоскости

и одновременно перпендикулярную к другой плоскости.

Рассмотрим построение взаимно перпендикулярных плоскостей на

чертеже. Пусть требуется провести плоскость через отрезок прямой DE

(D1E1, D2E2), перпендикулярную плоскости, заданной треугольником АВС

(А1В1С1, А2В2С2). Задача будет решена, если из точки D отрезка DE про-

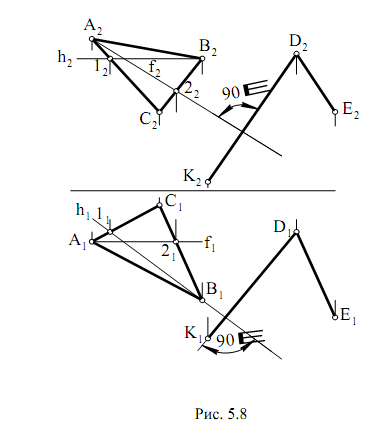
вести прямую перпендикулярно к треугольнику АВС (рис. 5.8). Для этого в треугольнике АВС проводим фронталь и горизонталь. Затем из точки D1

проводим перпендикуляр D1K1 к h1 (горизонтальная проекция горизонта-

ли), а из точки D2 – перпендикуляр D2K2 к f2 (фронтальная проекция фронтали). Таким образом, плоскость, заданная двумя пересекающимися прямыми (KD ∩ DE), перпендикулярна треугольнику АВС, т.к. проходит через

перпендикуляр к нему DK.

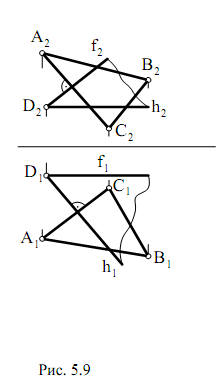
Рассмотрим второй случай. Пусть требуется из точки D провести

плоскость перпендикулярно к стороне АС треугольника АВС (рис. 5.9). Иными словами, чтобы сторона АС была перпендикулярна новой

плоскости, проходящей через точку D, А1С1 должна быть перпендикулярна

горизонтальной проекции горизонтали (h1), а А2С2 – перпендикулярна

фронтальной проекции фронтали f2 новой плоскости (h ∩ f). Поэтому из

точки D1 проводим h1 перпендикулярно А1С1 (h2 пройдет параллельно оси

Х), а из точки D2 проводим перпендикуляр к f2 (f1 пройдет параллельно оси

Х). Данные плоскости взаимно перпендикулярны, т.к. плоскость (f ∩ h)

проходит перпендикулярно стороне АС треугольника АВС.

Прямая и плоскость:

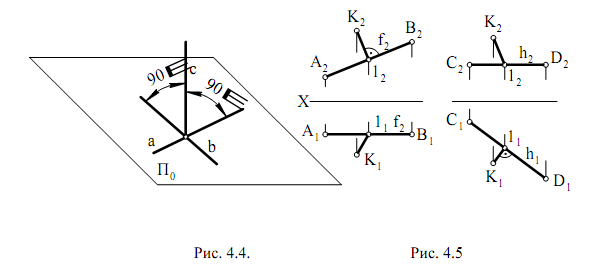
Прямая линия перпендикулярна плоскости, если она перпендикуляр-

на двум пересекающимся прямым этой плоскости (рис. 4.4).

На комплексном чертеже легко построить проекции прямого угла

между прямой общего положения и линией уровня (фронталью, горизонталью). На основании свойств прямого угла прямой угол проецируется в натуральную величину, например, на П2, если одна из его сторон параллельна этой плоскости проекций, т.е. является фронталью. Чтобы прямой угол проецировался на П1 без искажения, необходимо, чтобы одна из его сторон была параллельна П1, т.е. была горизонталью. На рис. 4.5 показано, как проведен перпендикуляр из точки К к фронтали и горизонтали.

Если задать плоскость двумя пересекающимися прямыми (АВ ∩ АD),

одна из которых будет фронталью, а вторая – горизонталью и провести из точки А2 перпендикуляр к А2В2, т.е. к фронтальной проекции фронтали, а из А1 – перпендикуляр к А1D1, т.е. к горизонтальной проекции горизонтали, то этот отрезок будет перпендикулярен заданной плоскости (рис. 4.6). Для того чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы на чертеже ее горизонтальная проекция была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой – перпендикулярна фронтальной проекции фронтали.

В случае, если плоскость задана следами, то, учитывая, что горизонтальная проекция горизонтали (h1) всегда параллельна горизонтальному

следу Г1, а фронтальная проекция фронтали параллельна фронтальному

следу Г2, то, чтобы из точки К (К1, К2) провести прямую перпендикулярно

плоскости Г (рис. 4.7), необходимо ее горизонтальную проекцию провести

перпендикулярно горизонтальному следу Г1, а фронтальную проекцию –

перпендикулярно фронтальному следу Г2.