19. Дифференцирование сложной функции

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке , а функция g имеет производную в точке , то сложная функция h(x) = g(f(x)) также имеет производную в точке .

Пусть даны функции, определённые в окрестностях на числовой прямой, где и Пусть также эти функции дифференцируемы: Тогда их композиция также дифференцируема: и её производная имеет вид:

Замечание

В обозначениях Лейбница цепное правило для вычисления производной функции где принимает следующий вид:

Инвариантность формы первого дифференциала

Дифференциал функции в точке имеет вид:

где  — дифференциал тождественного отображения :

Пусть теперь Тогда , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

Пример

Пусть Тогда функция может быть записана в виде композиции где

Дифференцируя эти функции отдельно:

получаем

20 Похідні та диференціали вищих порядків. Формула Лейбніца.

Нехай функція  диференційовна на проміжку X, а   її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної  називається похідною другого порядку функції  і позначається одним із символів:

.

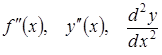Так у фізиці, якщо   закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то  є прискоренням цієї точки в момент часу t.

Аналогічно 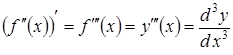 і т. д.

Взагалі похідною n-го порядку від функції  називається похідна від похідної -го порядку і позначається

, або , або .

 

Зауваження. При , похідну n-го порядку позначають відповідно ; при  позначають:  або .

Приклад 3.17. Знайти похідну другого порядку від функції

.

Розв’язання. Знаходимо спочатку  за формулою .

.

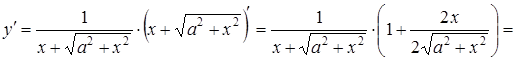
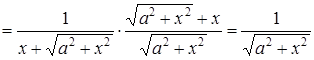Знаходимо похідну від отриманої функції:

, тобто .

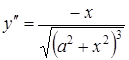Формула Лейбніца. Якщо функції ,  мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:

.         (3.14)

Похідні вищих порядків від функцій, заданих параметрично.

Якщо функції  і  параметрично задають функцію , то похідні 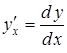, , 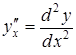можна послідовно обчислити за формулами:

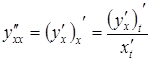,  і т. д.

Так, для похідної другого порядку має місце формула:

.                               (3.15)

Диференціали вищих порядків. Нехай функція  диференційовна на проміжку X. Її диференціал

називається також диференціалом першого порядку і його можна розглядати як функцію змінної x (приріст аргументу  вважається сталим).

Означення 3.4. Диференціалом другого порядку (second differential) функції  в точці x називається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім ) і позначається :

.

За означенням маємо

,

позначають . Таким чином

.                                     (3.16)

Аналогічно, диференціалом n-го порядку (позначається ), n=2,3,... називається диференціал від диференціала порядку  за умови, що в диференціалах весь час беруться одні й ті самі прирости  незалежної змінної x. Тобто

.

При цьому справедлива формула:

.                                     (3.17