- •1. Дійсні числа. Числові множини.
- •2. Поняття множини. Операції над множинами.
- •3. Поняття множини. Властивості операцій над множинами.
- •4. Числова послідовність, підпослідовність.
- •5. Границя послідовності.
- •6. Основні властивості границь числових послідовностей.
- •7. Число .
- •8. Обчислення границь числових послідовностей.
- •9. Поняття функції
- •10. Классификация функций. Основные элементарные функции.
- •11. Загальне поняття границі функції в точці та його окремі випадки.
- •12. Основні властивості границь функцій.
- •13. Нескінченно малі та великі функції, їх порівняння та застосування. А) Сравнение бесконечно малых функций
- •B) Сравнение бесконечно больших функций
- •14. Дві істотні границі та наслідки з них.
- •15. Поняття неперервної функції та її властивості.
- •Глобальные
- •16. Односторонняя непрерывность
- •17. Точки разрыва функции и их классификация
- •18. Понятие производной и дифференциала
- •19. Дифференцирование сложной функции
- •20 Похідні та диференціали вищих порядків. Формула Лейбніца.
- •Формула Ньютона-Лейбница
- •21.Правила Лопіталя розкриття невизначеностей
- •22. Формули Тейлора та Маклорена.
- •23 Ознаки монотонності функції.
- •24. Екстремум функції.
- •Проте виявляється, що цього недостатньо, бо може , а функція в цій точці екстремуму не має.
- •Якщо в критичній точці, то нічого конкретного сказати не можна, бо в цій точці може бути екстремум, а може й не бути.
- •25. Умова опуклості або угнутості кривої.
- •26. Асимптоти кривої. Побудова графіка функції.
- •27. Застосування правил Лопіталя до обчислення границь функцій.
- •Тема 3. Диференціальне числення функції однієї змінної
- •28. Необхідні та достатні умови екстремуму функції.
- •29. Розкладення за формулою Маклорена деяких елементарних функцій.
- •31. Поняття первісної функції та невизначеного інтеграла. Таблиця основних інтегралів.
- •32. Основні методи інтегрування: метод розкладення, метод підстановки (заміни змінної) та метод інтегрування частинами.
- •33. Поняття визначеного інтеграла. Обчислення визначеного інтеграла.
- •34. Заміна змінної та інтегрування частинами у визначеному інтегралі. Застосування визначеного інтеграла.
- •35. Невласні інтеграли першого роду.
- •Невласні інтеграли першого роду ("нескінчений інтервал")
- •36. Невласні інтеграли другого роду.Невласні інтеграли
- •37. Ознака збіжності невласних інтегралів.
- •38. Поняття числового ряду та його суми.
- •39. Основні властивості рядів.
- •40. Критерій Коші збіжності ряду.
- •40. Критерій Коші збіжності ряду.
- •41. Ознаки збіжності додатних рядів: порівняння, д’Аламбера, Коші, інтегральна ознака Коші.
- •42. Функціональні послідовності та ряди.
- •49. Неперервність функцій декількох змінних
- •50. Частинні похідні функції декількох змінних.
- •51. Полный дифференциал функции нескольких переменных.
- •52. Означення подвійного та повторного інтегралів. Обчислення подвійного інтеграла.
- •53. Заміна змінних у подвійному інтегралі.
- •55. Криволинейный интеграл первого рода
- •56. Криволинейный интеграл второго рода
- •57. Производная по направлению. Градиент. Уравнение касательной плоскости к поверхности. Уравнение нормали
- •58. Екстремум функції двох змінних.
- •59. Найбільше та найменше значення функції багатьох змінних у замкненій області.
17. Точки разрыва функции и их классификация
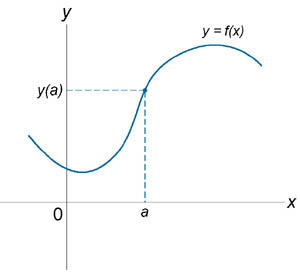
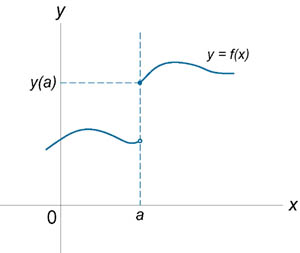
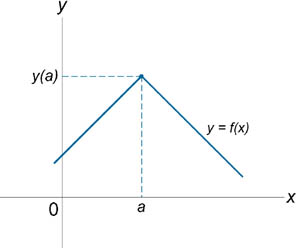
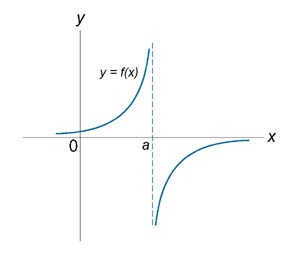
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|
|
|
|||
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
|||
|
|
|
|
|||
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
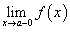 и
правосторонний предел
и
правосторонний предел
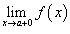 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов
![]() называется
скачком
функции.
называется
скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
18. Понятие производной и дифференциала
Определение
21.1 Пусть функция
![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки
![]() и
и
![]() -
произвольная точка из этой окрестности.
Тогда если выражение
-
произвольная точка из этой окрестности.
Тогда если выражение
![]() имеет
предел при
имеет
предел при
![]() ,
то этот предел называется производной
функции
в
точке
(обозначается
,
то этот предел называется производной
функции
в
точке
(обозначается
![]() ).
).
Определение
21.2 Пусть функция
определена
в некоторой левой (правой) полуокрестности
точки
и
-
произвольная точка из этой полуокрестности.
Тогда если выражение
имеет
левый (правый) предел при
,
то этот предел называется левой
(правой) производной
функции
в
точке
(обозначается
![]() ).
).
Если
функция определена на некотором
промежутке и в каждой его точке существует
ее производная, то эта производная,
очевидно, является функцией, определенной
на данном промежутке (обозначается
![]() ).
).
Определение
21.3 Функция
,
определенная в некоторой окрестности
точки
,
называется дифференцируемой в
этой точке, если ее приращение
![]() ,
,
![]() представимо
в виде
представимо
в виде
![]() .
Слагаемое
.
Слагаемое
![]() называется
дифференциалом функции
в
точке
(обозначается
называется
дифференциалом функции
в
точке
(обозначается
![]() или
или
![]() ).
).
Определение
21.4 Пусть функция
определена
на промежутке
![]() и
имеет производную
в
каждой его точке. Если функция
имеет
производную в точке
и
имеет производную
в
каждой его точке. Если функция
имеет
производную в точке
![]() ,
то она называется второй производной
функции
в
точке
(обозначается
,
то она называется второй производной
функции
в
точке
(обозначается
![]() или
или
![]() ).
Аналогично определяется производная
n-го порядка
).
Аналогично определяется производная
n-го порядка
![]() .
.
Таблица производных основных элементарных функций