5. Границя послідовності.

Границя числової послідовності — фундаментальне поняття математичного аналізу, число, до якого члени послідовності прямують зі збільшенням індекса в сенсі наступного означення:

Дійсне число a називається границею числової послідовності  , якщо  ^[1]

Позначення:   або 

При цьому також кажуть, що послідовність   збігається до числа a, або має границю a. Послідовність, що збігається до деякої границі називається збіжною, в інших випадках — розбіжною.

6. Основні властивості границь числових послідовностей.

Основнi властивостi границь

1. Збереження знаку функцiєю, що має границю у точцi.

2. Граничний перехiд i арифметичнi операцiї.

3. Границя композицiї функцiй.

4. Граничний перехiд i нерiвностi.

(потом идут дальше теоремы и пиздец как много текста ,так что я их не кидал)

7. Число .

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Число e может быть определено несколькими способами.

• Через предел:

 (второй замечательный предел).

• Как сумма ряда:

 или  .

• Через определённый интеграл:

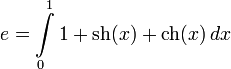
• Как единственное число a, для которого выполняется

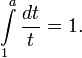
• Как единственное положительное число a, для которого верно

8. Обчислення границь числових послідовностей.

Арифметичні дії над послідовностями

9. Поняття функції

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения , а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

10. Классификация функций. Основные элементарные функции.

Функции:

I. Неэлементарные

II. Элементарные

1. трансцендентные (sinx, cosx, tgx…)

2. алгебраические

а) иррациональные

б) рациональные (целые, дробно-рациональные)

Основные элементарные функции:

1. y = xⁿ nЭQ степенная функция

2. y = a^x показательная

3. y = log _a x, где  a – постоянное положительное число, не равное 1 логарифмическая

4. y = sin x y = cos x … тригонометрическая

5. y = Arcsinx y = Arccosx

Обратные тригонометрическим

Элементарной называется функия, которую можно задать одним аналитическим выражением составленным из основных элементарных функций с помощью 4-х арифметических действий и опрераций взятия функции от функций последовательно примененных конечное число раз