53. Заміна змінних у подвійному інтегралі.

55. Криволинейный интеграл первого рода

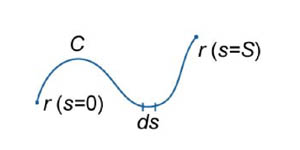
Пусть кривая C описывается векторной функцией , где переменная s представляет собой длину дуги кривой (рисунок 1).

Если на кривой C определена скалярная функция F, то интеграл 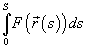называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как

Криволинейный интеграл существует, если функция F непрерывна на кривой C.

Рис.1		Рис.2

Свойства криволинейного интеграла первого рода

Криволинейный интеграл I рода обладает следующими свойствами:

1. Интеграл не зависит от ориентации кривой;

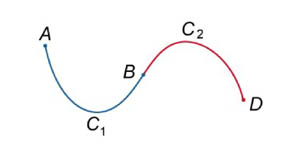
2. Пусть кривая C₁ начинается в точке A и заканчивается в точке B, а кривая C₂ начинается в точке B и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться кривая C₁ U C₂, которая проходит от A к B вдоль кривой C₁ и затем от B к D вдоль кривой C₂. Для криволинейных интегралов первого рода справедливо соотношение

3. Если гладкая кривая C задана параметрически соотношением 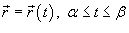и скалярная функция F непрерывна на кривой C, то

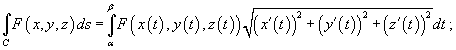
4. Если C является гладкой кривой в плоскости Oxy, заданной уравнением 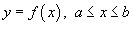, то

5. Если гладкая кривая C в плоскости Oxy определена уравнением 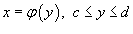, то

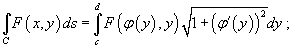
6. В полярных координатах интеграл 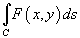выражается формулой

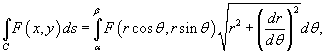
где кривая C задана в полярных координатах функцией .

56. Криволинейный интеграл второго рода

Пусть функции P(x, y) и Q(x, y) непрерывны в точках дуги АВ гладкой кривой К, имеющей уравнение , .

О п р е д е л е н и е. Интегральной суммой для функций P(x, y) и Q(x, y) по координатам называется сумма вида

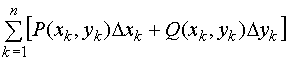, (131)

где - проекции элементарной дуги на оси Ох и Оу.

О п р е д е л е н и е. Криволинейным интегралом по координатам (или криволинейным интегралом второго рода) от выражения P(x, y)dx + Q(x, y)dy по направленной дуге АВ называется конечный предел интегральной суммы (131) при стремлении и к нулю.

Это обозначается так:

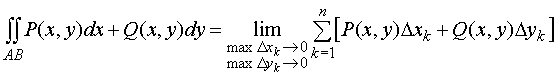. (132)

Физическое истолкование криволинейного интеграла 2-го рода Криволинейный интеграл 2-го рода есть работа, совершаемая переменной силой на криволинейном пути АВ.

57. Производная по направлению. Градиент. Уравнение касательной плоскости к поверхности. Уравнение нормали

Вектор с координатами , ,  называется градиентом функции u = f (x, y, z) в точке M(x, y, z) и обозначается grad u = + + .

Под производной функции u = f (x, y, z) в данном направлении  понимается выражение  = cosa + cosb + cosg, где cosa, cosb, cosg – направляющие косинусы вектора  

 

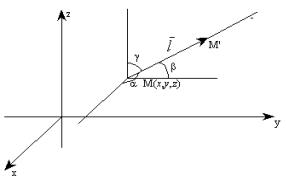
 Производная  представляет собой скорость изменения функции в данном направлении.

Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению.

Градиент функции в данной точке указывает напрвление наиболее быстрого возрастания функции.

Величина градиента, т.е. | grad u | =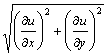 обозначается tg j и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

Пусть М – точка поверхности S. Плоскость, содержащая точку М и обладающая тем свойством, что расстояние от этой плоскости до переменной точки M₁ поверхности S является бесконечно малым по сравнению с расстоянием ММ₁, называется касательной плоскостью к поверхности S в точке М. Если поверхность в трехмерном пространстве задана уравнением f(x; y; z) = 0, где функция f достаточное число раз дифференцируема, то уравнение плоскости, касательной к этой поверхности в точке М(х_М; у_М; z_М), имеет вид:

, (**)

где  – частные производные функции трех переменных f(x; y; z) по этим переменным. Если же поверхность задана уравнением, разрешенным относительно аппликаты z, т.е. имеет вид z = z(x; y), то уравнение (**) касательной плоскости  принимает вид:

(конечно, предполагается, что функция z имеет непрерывные первые частные производные).

Нормаль (франц. normal, от лат. normalis — прямой) к кривой (к поверхности) в данной её точке — прямая, проходящая через эту точку и перпендикулярная к касательной

прямой (касательной плоскости) в этой же точке кривой (поверхности). Плоская кривая имеет в каждой точке единственную Нормаль, расположенную в плоскости кривой. Если х = f (t) и у = g (t) — параметрические уравнения плоской кривой L, то уравнение Нормаль в точке (x0, y0) кривой L, соответствующей значению t0 параметра t, может быть записано в виде: 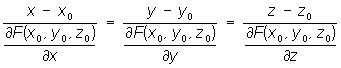. Для плоской кривой, заданной уравнением F (х, у) = 0, уравнение Нормаль имеет вид:   .   Пространственная кривая имеет в каждой своей точке бесчисленное множество Нормаль, заполняющих некоторую плоскость (нормальную плоскость). Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Нормаль, перпендикулярную к соприкасающейся плоскости, называется бинормалью. Касательная, главная Нормаль и бинормаль образуют подвижный триэдр кривой.   Для поверхности, заданной уравнением F (х, у, z) = 0, Нормаль может быть представлена уравнениями:   .   Понятие Нормаль играет существенную роль не только в дифференциальной геометрии, но и в различных её приложениях: в геометрической оптике (например, в формулировке основных законов преломления и отражения световых лучей), в механике (материальная точка или тело при перемещениях по гладким линиям или поверхностям испытывают реакцию, направленную по Нормаль, в консервативном поле силовые линии в каждой точке имеют направление Нормаль к изопотенциальной поверхности, проходящей через эту точку, и т.д.).