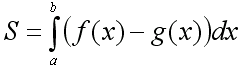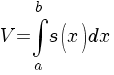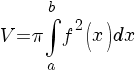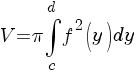- •1. Дійсні числа. Числові множини.
- •2. Поняття множини. Операції над множинами.
- •3. Поняття множини. Властивості операцій над множинами.
- •4. Числова послідовність, підпослідовність.
- •5. Границя послідовності.
- •6. Основні властивості границь числових послідовностей.
- •7. Число .
- •8. Обчислення границь числових послідовностей.
- •9. Поняття функції
- •10. Классификация функций. Основные элементарные функции.
- •11. Загальне поняття границі функції в точці та його окремі випадки.
- •12. Основні властивості границь функцій.
- •13. Нескінченно малі та великі функції, їх порівняння та застосування. А) Сравнение бесконечно малых функций
- •B) Сравнение бесконечно больших функций
- •14. Дві істотні границі та наслідки з них.
- •15. Поняття неперервної функції та її властивості.
- •Глобальные
- •16. Односторонняя непрерывность
- •17. Точки разрыва функции и их классификация
- •18. Понятие производной и дифференциала
- •19. Дифференцирование сложной функции
- •20 Похідні та диференціали вищих порядків. Формула Лейбніца.
- •Формула Ньютона-Лейбница
- •21.Правила Лопіталя розкриття невизначеностей
- •22. Формули Тейлора та Маклорена.
- •23 Ознаки монотонності функції.
- •24. Екстремум функції.
- •Проте виявляється, що цього недостатньо, бо може , а функція в цій точці екстремуму не має.
- •Якщо в критичній точці, то нічого конкретного сказати не можна, бо в цій точці може бути екстремум, а може й не бути.
- •25. Умова опуклості або угнутості кривої.
- •26. Асимптоти кривої. Побудова графіка функції.
- •27. Застосування правил Лопіталя до обчислення границь функцій.
- •Тема 3. Диференціальне числення функції однієї змінної
- •28. Необхідні та достатні умови екстремуму функції.
- •29. Розкладення за формулою Маклорена деяких елементарних функцій.
- •31. Поняття первісної функції та невизначеного інтеграла. Таблиця основних інтегралів.
- •32. Основні методи інтегрування: метод розкладення, метод підстановки (заміни змінної) та метод інтегрування частинами.
- •33. Поняття визначеного інтеграла. Обчислення визначеного інтеграла.
- •34. Заміна змінної та інтегрування частинами у визначеному інтегралі. Застосування визначеного інтеграла.
- •35. Невласні інтеграли першого роду.
- •Невласні інтеграли першого роду ("нескінчений інтервал")
- •36. Невласні інтеграли другого роду.Невласні інтеграли
- •37. Ознака збіжності невласних інтегралів.
- •38. Поняття числового ряду та його суми.
- •39. Основні властивості рядів.
- •40. Критерій Коші збіжності ряду.
- •40. Критерій Коші збіжності ряду.
- •41. Ознаки збіжності додатних рядів: порівняння, д’Аламбера, Коші, інтегральна ознака Коші.
- •42. Функціональні послідовності та ряди.
- •49. Неперервність функцій декількох змінних
- •50. Частинні похідні функції декількох змінних.
- •51. Полный дифференциал функции нескольких переменных.
- •52. Означення подвійного та повторного інтегралів. Обчислення подвійного інтеграла.
- •53. Заміна змінних у подвійному інтегралі.
- •55. Криволинейный интеграл первого рода
- •56. Криволинейный интеграл второго рода
- •57. Производная по направлению. Градиент. Уравнение касательной плоскости к поверхности. Уравнение нормали
- •58. Екстремум функції двох змінних.
- •59. Найбільше та найменше значення функції багатьох змінних у замкненій області.
34. Заміна змінної та інтегрування частинами у визначеному інтегралі. Застосування визначеного інтеграла.
Замена
переменной в определённом интеграле.
Теорема.
Пусть функция
![]()
определена, непрерывно дифференцируема и монотонна на отрезке
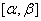 ,
, ,
,функция
 непрерывна
на отрезке [a,
b].
непрерывна
на отрезке [a,
b].
Тогда
 .
.
![]() Док-во.
Пусть F(x)
- первообразная для функции f(x),
т.е.
Док-во.
Пусть F(x)
- первообразная для функции f(x),
т.е.
![]() ,
тогда
,
тогда
![]() -
первообразная для функции
-
первообразная для функции
![]() .
.
 ,
что и требовалось доказать.
,
что и требовалось доказать.
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла. Пример:
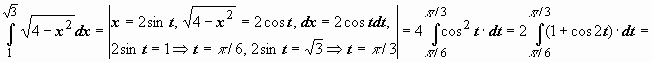
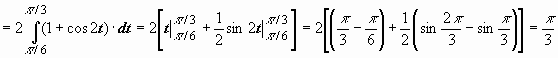 .
.
Формула
интегрирования по частям для определённого
интеграла.
Если u(x),
v(x)
- непрерывно дифференцируемые функции,
то
 .
Док-во.
Интегрируем равенство
.
Док-во.
Интегрируем равенство
![]() в
пределах от a
до b:
в
пределах от a
до b:
 .
Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница
.
Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница
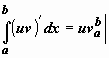 ,
следовательно,
,
следовательно,
 ,
откуда и следует доказываемое равенство.
Пример:
,
откуда и следует доказываемое равенство.
Пример:
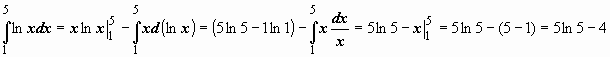
Застосування інтегралу
Інтегральне числення широко використовується при розв’язуванні різноманітних практичних задач. Розглянемо деякі з них.
|
||||||||
Обчис Обчислення площі криволінійної трапеції
Обчислення об’ємів тіл
|
35. Невласні інтеграли першого роду.
Невласти́вий інтегра́л є розширенням поняття визначений інтеграл; він дозволяє в деяких випадках обраховувати «інтеграл на нескінченості» або «інтеграл від необмеженої функції». В математичному аналізі невластивим інтервалом називають границю послідовності визначених інтегралів, коли інтервал інтегрування збільшується до нескінченості, або коли інтервал наближається до особливої точки інтегрованої функції, де та йде у нескінченість.
Невласні інтеграли першого роду ("нескінчений інтервал")
Нехай
функція
![]() неперервна на проміжку
неперервна на проміжку
![]() .
Тоді вона буде неперервною на будь-якому
скінченому відрізку
.
Тоді вона буде неперервною на будь-якому
скінченому відрізку
![]() .
Для функції
,
неперервної на
,
існує визначений інтеграл
.
Для функції
,
неперервної на
,
існує визначений інтеграл
![]() ,
який залежить від верхньої межі
інтегрування. Цей інтеграл визначає
деяку величину, наприклад площу
криволінійної трапеції, обмеженої
,
який залежить від верхньої межі
інтегрування. Цей інтеграл визначає
деяку величину, наприклад площу
криволінійної трапеції, обмеженої
графіком
функції
![]() прямими
прямими
![]() ,
,
![]() ,
,
![]() .
Будемо необмежено збільшувати верхню
межу інтегрування
.
Будемо необмежено збільшувати верхню
межу інтегрування
![]() .
При цьому можливі два випадки: або
.
При цьому можливі два випадки: або
![]() при
при
![]() має скінчену границю, або не має.
має скінчену границю, або не має.