32. Основні методи інтегрування: метод розкладення, метод підстановки (заміни змінної) та метод інтегрування частинами.

Інтегрування раціональних дробів. Метод розкладання.

Невизначений інтеграл від будь-якого раціонального дробу на всякому проміжку, на якому знаменник дробу не звертається в нуль, існує і виражається через елементарні функції, а саме він є алгебраїчною сумою суперпозиції раціональних дробів, арктангенсів і раціональних логарифмів.

Сам метод полягає в розкладанні раціонального дробу на суму найпростіших.

Усякий правильний раціональний дріб , знаменник якого розкладений на множники

можна представити (і притім єдиним образом) у виді наступної суми найпростіших дробів:

де - деякі дійсні коефіцієнти. Звичайно невідомі коефіцієнти знаходяться за допомогою методу невизначених коефіцієнтів.

Метод підстановки (заміни змінної)

Цей метод містить два прийоми.

a) Якщо для знаходження заданого інтеграла ∫f(x)dx зробити підстановку x = φ(t), тоді має місце рівність

Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба; щоб функція х - φ (t) мала обернену t = ψ(х).

Приклад. Знайти інтеграл

Розв'язування. Зробимо підстановку х = 5sint, тоді

Отже, одержимо

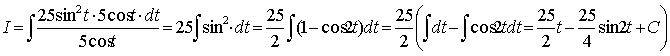
Із рівності х = 5sin t одержимо t = arcsin (х/5);

Отже,

b) Якщо зробити заміну змінної, тобто t = φ (х) тоді має місце

рівність

Після знаходження останнього інтеграли треба повернутись до змінної х, використовуючи рівність t = φ (х).

Приклад. Знайти

Розв’язування. Нехай тоді

Тому

Метод інтегрування частинами

Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).

Формула інтегрування частинами:

Ця формула дозволяє знаходження інтеграла звести до зна­ходження інтеграла . При вдалому обранні u то dv інтеграл може бути табличним або простішим ніж заданий інтеграл

Приклад. Знайти

Розв'язування. Нехай u = Inx, dv = dx. Тоді v = x

За формулою інтегрування частинами одержимо

33. Поняття визначеного інтеграла. Обчислення визначеного інтеграла.

Означення.

Гранця інтегральної суми коли n→∞ називається визначеним інтегралом, і записується це так : .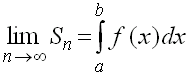

читається: "інтеграл від a до b f від xdx"

Число а називається нижньою межею інтегрування, b – верхньою межею інтегрування, відрізок [a; b] – проміжок інтегрування.

Властивості визначеного інтегралу

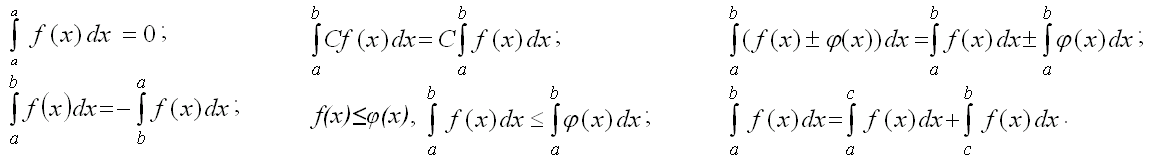
Формула Ньютона-Лейбніца

Визначений інтеграл тісно пов’язаний із первісною та невизначеним інтегралом формулою Ньютона- Лейбніца

.

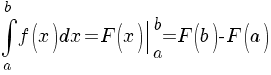Інтеграл Рімана

Інтеграл Рімана - найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної , визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки інтегральна сума визнається як

де - будь-яка точка з відрізку.

Якщо існує границя таких сум при прямуванні найбільшої довжини відріку до нуля, то функція називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку і позначається

.

Інтеграл Рімана

Інтеграл Рімана - найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної , визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки інтегральна сума визнається як

де - будь-яка точка з відрізку.

Якщо існує границя таких сум при прямуванні найбільшої довжини відріку до нуля, то функція називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку і позначається

.