Модуль 2 упругие волны

Комплексная цель данного модуля - Сообщить студенту основные законы раздела «Упругие волны» и их математическое выражение, познакомить студентов с методикой решения задач по теме «Упругие волны», сформировать навыки самостоятельного решения задач.

Основные формулы

Связь длины волны λ, периода колебаний Т и частоты υ

,

где V – скорость распространения колебаний в среде (фазовая скорость).

Волновое число

,

где V — скорость волны; Т— период колебаний; ω— циклическая частота волны.

Поток энергии

,

где Е – энергия волны.

Плотность потока энергии волны

,

где V — скорость волны; — объемная плотность энергии колебательного движения.

Вектор Умова (вектор плотности потока энергии)

.

Уравнение плоской волны, распространяющейся вдоль положительного направления оси х

,

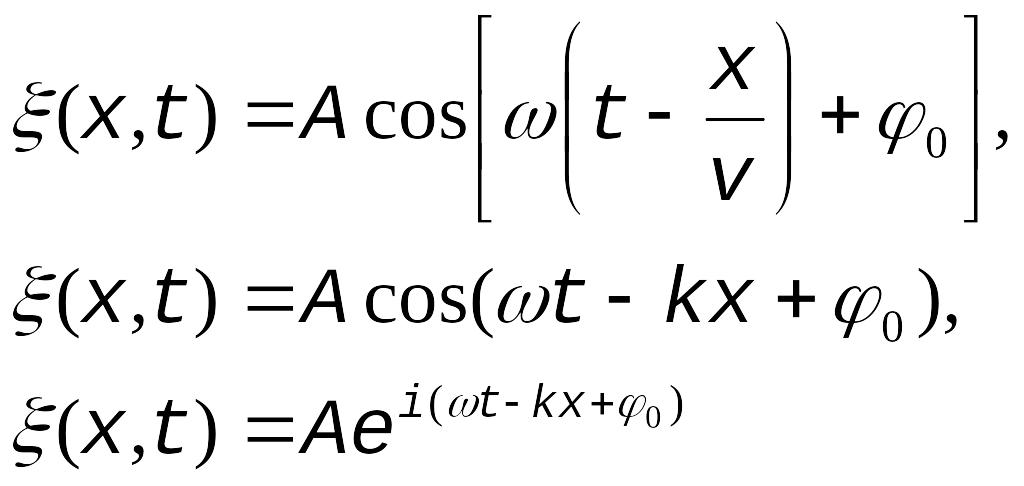где — смещение точек среды с координатой x в момент времени t; А — амплитуда волны; ω — циклическая (круговая) частота; V— фазовая скорость; — начальная фаза колебаний; - волновое число; T – период колебаний.

Уравнение сферической волны

.

Волновое уравнение

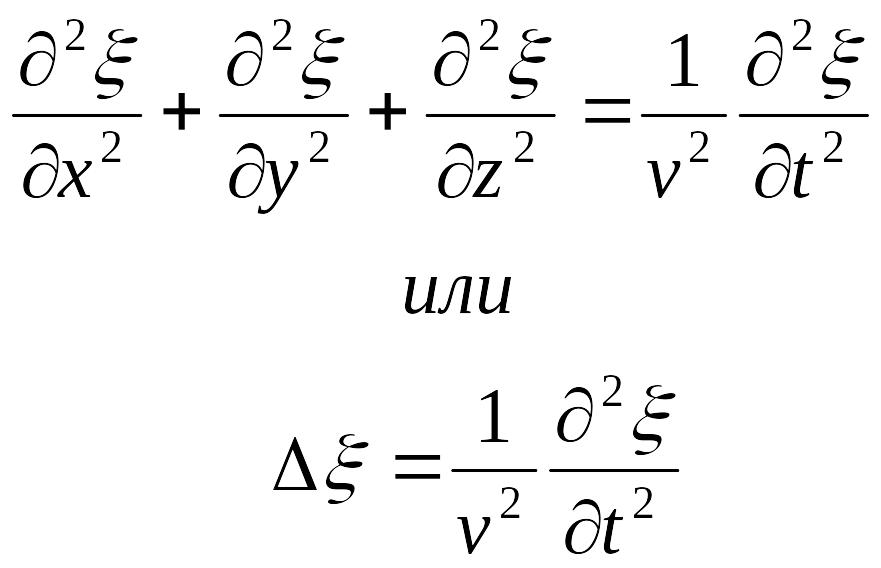
где V — фазовая скорость; - оператор Лапласа.

Волновое уравнение для плоской волны, распространяющейся вдоль оси х

.

Решение – уравнение плоской волны .

Связь между разностью фаз Δφ и разностью хода Δ

.

Условия максимума и минимума амплитуды при интерференции волн

Δ_max= ;

Δ_min= ,

где m=0,1,2,… .

Уравнение стоячей волны

.

Амплитуда стоячей волны

.

Пучности стоячей волны

.

Узлы стоячей волны

.

Координаты пучностей и узлов

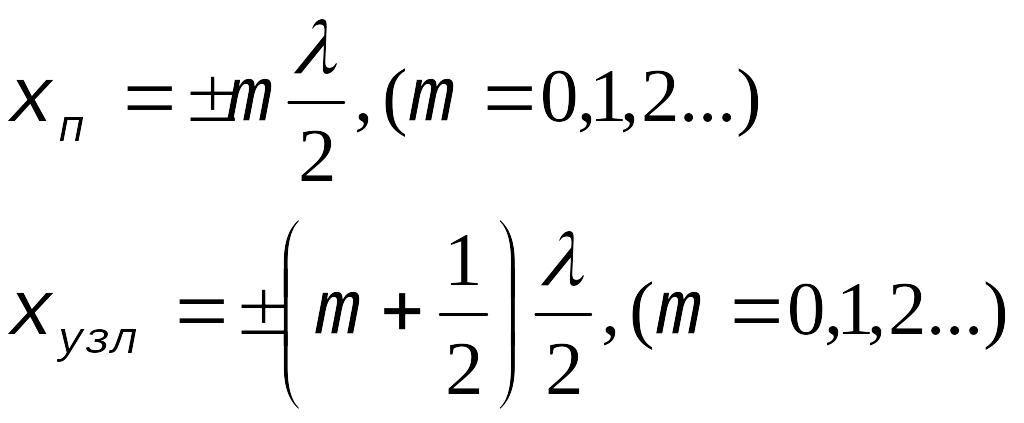
Уровень интенсивности звука (Б)

L=lg ,

где I — интенсивность звука; I₀ — интенсивность звука на пороге слышимости (I₀=1пВт/м²).

Скорость распространения звуковых волн в газах

,

где R — молярная газовая постоянная; М — молярная масса газа; γ=Ср/Cv—отношение молярных теплоемкостей газа при постоянных давлении и объеме; Т — термодинамическая температура.

Эффект Доплера в акустике

,

где υ — частота звука, воспринимаемая движущимся приемником; υ₀ — частота звука, посылаемая источником; v_пр — скорость движения приемника; v_ист — скорость движения источника; v — скорость распространения звука. Верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак — в случае их взаимного удаления.

Методика решения задач

Задача 1 Колеблющиеся точки, находящиеся на одном луче, удалены: от источника колебания на x₁=6м и х₂=8,7м и колеблются с разностью фаз Δφ=3π/4. Период колебания источника Т=10^-2с. Чему равна длина волны и скорость распространения колебаний в данной среде? Составить уравнение волны для первой и второй точек, считая амплитуды колебаний точек равными А=0,5м.

Решение Длину волны λ определяем из уравнения волны по разности фаз Δφ и расстоянию точек от источника. Это уравнение может быть записано в таком виде:

(25)

(26)

В уравнении (26) выражение является фазой колебания. Запишем фазы для каждой из точек

(27)

Определим разность фаз

(28)

Из уравнения (28) определяем длину волны

Подставляя заданные значения, получим

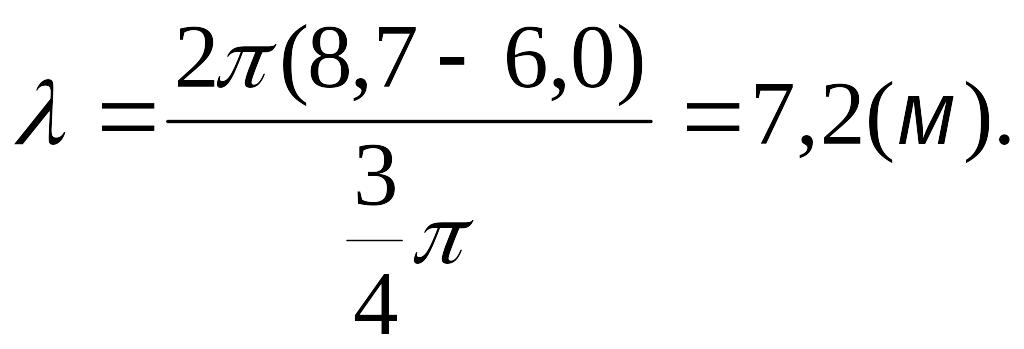
Скорость распространения волны находим из известной формулы . Определяем числовое значение скорости:

Циклическая частота ω определяется из соотношения:

Подставляя числовые значения в уравнение (25), получаем уравнения волны, отображающие колебания первой и второй точек:

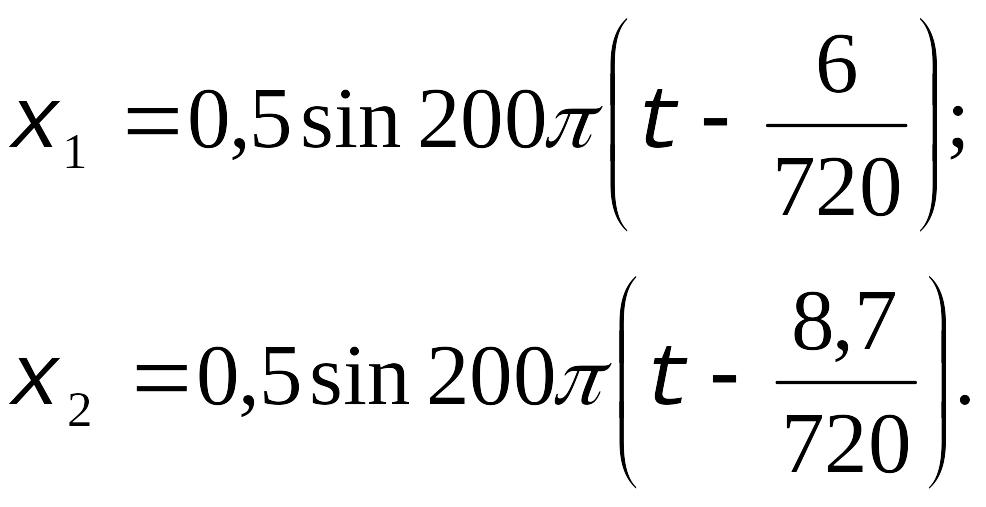
Задача 2 Уравнение незатухающих колебаний дано в виде см. 1) Найти уравнение волны, если скорость распространения колебаний 300м/с. 2) Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии 600м от источника колебаний. 3) Написать и изобразить графически уравнение колебания для точек волны в момент t=4с после начала колебаний.

Решение 1) Уравнение волны в нашем случае имеет вид

см. (29)

Таким образом , т. е. смещение точек, лежащих на луче, зависит от времени и расстояния точки до источника колебаний.

2) Для точки, отстоящей от источника колебаний на 6м. уравнение (1) примет вид см. т. е. при =const мы получим — смещение фиксированной точки, лежащей на луче, меняется со временем.

3) При =4с уравнение (29) примет вид . В этом случае =const и - различные точки, лежащие на луче, имеют различное смещение в данный момент времени.

Задача 3 Два динамика расположены на расстоянии d=2,5м друг от друга и воспроизводят один и тот же музыкальный тон на определенной частоте, который регистрируется приемником, находящимся на расстоянии =3,5м от центра динамиков. Если приемник передвинуть от центральной линии параллельно динамикам на расстояние =1,55м, то он фиксирует первый интерференционный минимум. Скорость звука =340м/с. Определите частоту звука.

Решение Запишем условие интерференционного минимума

Для первого минимума

Расстояния от динамиков до приемника, фиксирующего первый минимум,

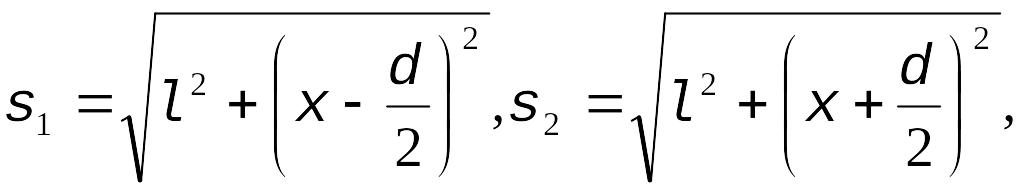
Частота колебаний

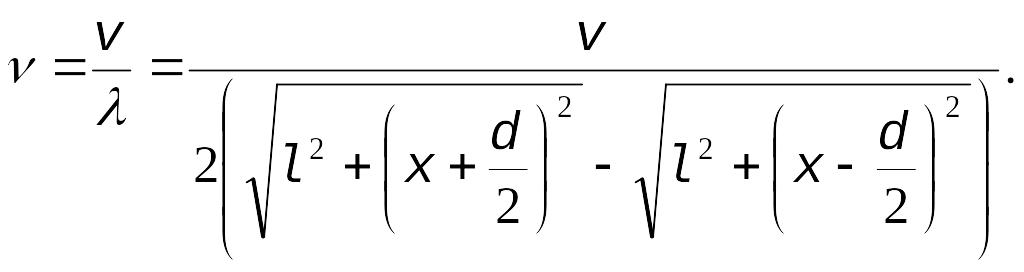
Вычисляя, получаем =175Гц.

Задача 4 Один конец упругого стержня соединен с источником гармонических колебаний, подчиняющихся закону , а другой его конец жестко закреплен. Учитывая, что отражение в месте закрепления стержня происходит от менее плотной среды, определите характер колебаний в любой точке стержня.

Решение Запишем уравнения падающей и отраженной волн

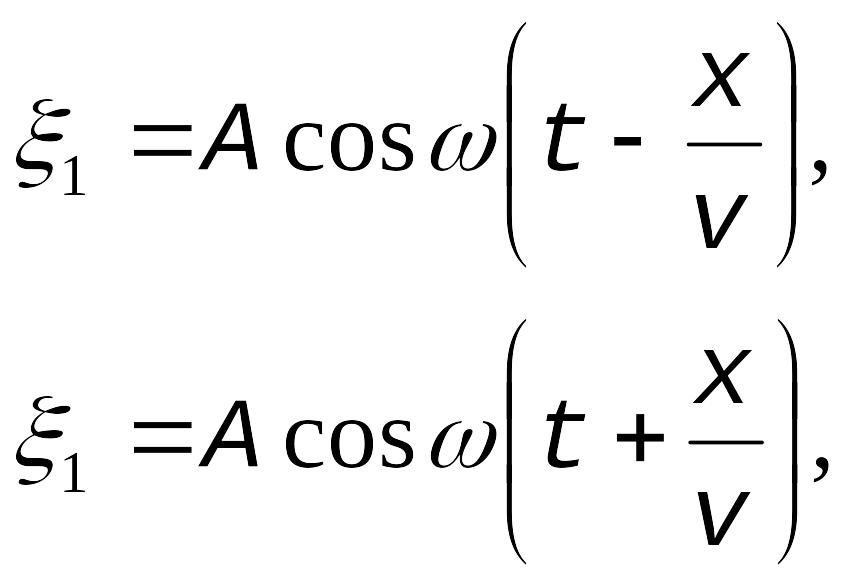
При наложении они образуют стоячую волну, уравнение которой

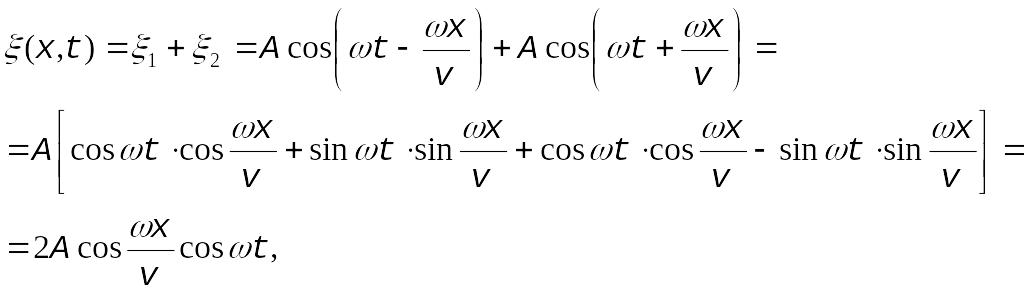
где

получаем

.

При - пучности.

При - узлы.

Задача 5 Неподвижный приемник при приближении источника звука, излучающего волны с частотой υ₀ =360Гц, регистрирует звуковые колебания с частотой υ=409Гц. Принимая температуру воздуха Т=290К, его молярную массу М=0,029кг/моль, Определите скорость движения источника звука.

Решение Исходя из общей формулы для эффекта Доплера в акустике и учитывая, что приемник покоится, а источник приближается к приемнику, получим

,

где v — скорость распространения звука. Отсюда

. (30)

Скорость распространения звуковых волн в газах

, (31)

где для воздуха γ= =1,4.

Подставив (31) в (30), найдем искомую скорость движения источника звука:

.

Вычисляя, получаем v_ист=34,1м/с.