Задачи для самостоятельного решения

1 Начертить на одном графике два гармонических колебания с одинаковыми амплитудами (А₁=А₂=2см) и одинаковыми периодами (Т₁=Т₂=8с), но имеющими разность фаз:

2 Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

3 Уравнение движения точки дано в виде . Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.

4 Уравнение колебания материальной точки массой m=1,6∙10^-2кг имеет вид м. Построить график зависимости от времени t (в пределах одного периода) силы F, действующей на точку. Найти значение максимальной силы.

5 Чему равно отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для моментов времени: 1) с, 2) с, 3) с. Начальная фаза колебаний равна нулю.

6 Определите отношение кинетической энергии Т точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

7 Для частицы из предыдущей задачи найти среднее значение вектора скорости : 1) за период колебания Т, 2) за первую четверть Т, 3) за вторую четверть Т.

8 Как, зная амплитуду смещения а и амплитуду скорости найти частоту гармонического колебания ω₀?

9 1) Найти уравнение, связывающее значения импульса р_х=тх со значениями координаты х одномерного гармонического осциллятора. Масса осциллятора т, частота ω, амплитуда колебания а. 2) Нарисовать кривую, описываемую этим уравнением. 3) Выразить площадь S, ограниченную этой кривой, через энергию осциллятора Е.

10 При подвешивании грузов массами m₁=600г и m₂=400г к свободным пружинам последние удлинились одинаково (l=10см). Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз.

11 Однородный диск радиусом R=20см колеблется около горизонтальной оси, проходящей на расстоянии l=15см от центра диска. Определите период T колебаний диска относительно этой оси.

12 Два математических маятника имеют одинаковую массу, длины, отличающиеся в n=1,5 раза, и колеблются с одинаковой угловой амплитудой. Определите, какой маятник обладает большей энергией и во сколько раз.

13 Найти закон, по которому изменяется со временем натяжение F нити математического маятника, совершающего колебание . Масса маятника равна m, длина l.

14 В неподвижной кабине лифта качается маятник. Вследствие обрыва троса кабина начинает падать с ускорением g. Как ведет себя маятник относительно кабины лифта, если в момент обрыва троса он

1) находился в одном из крайних положений,

2) проходил через положение равновесия?

15 Два одинаково направленных гармонических колебания одинакового периода с амплитудами А₁=4см и А₂=8см имеют разность фаз φ=45^о. Определить амплитуду результирующего колебания.

16 Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз 60°, равна А=6см. Определите амплитуду А₂ второго колебания, если А₁=5см.

17 Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями ,см и ,см. Определите уравнение траектории точки и вычертите ее с нанесением масштаба

18 Период затухающих колебаний Т=1с, логарифмический декремент затухания Θ=0,3, начальная фаза равна нулю. Смещение точки при t=2Т составляет 5см. Запишите уравнение движения этого колебания.

19 Докажите, что выражения для коэффициента затухания и циклической частоты 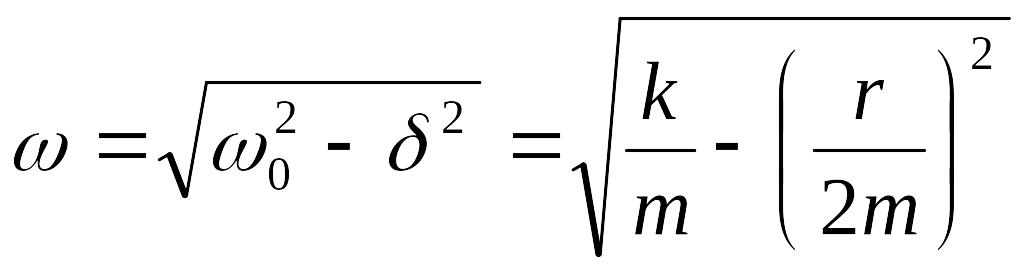>0 следуют из решения дифференциального уравнения для затухающих колебаний , (m – масса тела, r – коэффициент сопротивления, k – коэффициент упругости).

20 При наблюдении затухающих колебаний выяснилось, что для двух последовательных колебаний амплитуда второго меньше амплитуды первого на 60%. Период затухающих колебаний T=0,5с. Определите: 1) коэффициент затухания δ; 2) для тех же условий частоту v₀ незатухающих колебаний.

21 Тело массой m=100г, совершая затухающие колебания, за τ=1мин потеряло 40% своей энергии. Определите коэффициент сопротивления r.

22 Уравнение незатухающих колебаний дано в виде см.