2.4. Тепловой расчёт со и в
1). Построим функциональную схему котельной.
На рис.3 изображена функциональная схема котельной.
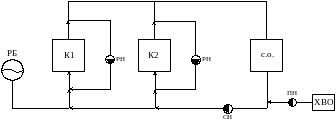
РН – рециркуляционный насос; РБ – расширительный бак; ПН – подпиточный насос; СН – сетевой насос; К1 – котел №1; К2 – котел №2; с.о – система отопления; ХВО – химводоочистка.
Рис.3. Функциональная схема котельной
2). Преобразуем функциональную схему в тепловую (см. рис.4)
950С
950С
2000кВт
2000кВт
950С
950С
К1
К1
950С
950С
800С
800С
700С
700С
700С
700С
Рис.4. Тепловая схема котельной
3). Преобразовываем тепловую схему в расчётный граф .
На рис.5 представлен расчётный граф.
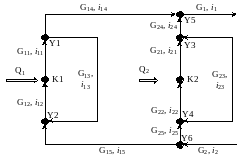
Рис.5. Расчётный граф
4). Составляем материальный и энергетический балансы для каждого узла графа. Для этого используем следующие уравнения:
- уравнение материального баланса (равенство расходов теплоносителя):
,
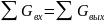(10)
где Gвх и Gвых – расход теплоносителя, соответственно, на входе и выходе из узла, кг/ч;
- уравнение энергетического баланса (равенство энергий):
,
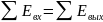(11)
где Евх и Евых – тепловая энергия, которой обладает теплоноситель, соответственно, на входе и выходе из энергетического объекта, кКал/ч:
,
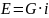(12)
где i – энтальпия теплоносителя, кКал/кг (причём i приблизительно равна температуре воды, °С).
Материальные и энергетические балансы для узлов графа имеют следующий вид:
K1: G12-G11=0
G12·i12-G11·i11=-Q1
K2: G22-G21=0
G22·i22-G21·i21=-Q2
Y1: G11-G14-G13=0
G11·i11-G14·i14-G13·i13=0
Y2: G15+G13-G12=0
G15·i15+ G13·i13-G12·i12=0
Y3: G21-G24-G23=0
G21·i21-G24·i24-G23·i23=0
Y4: G25+G23-G22=0
G25·i25+ G23·i23-G22·i22=0
Y5: G14+G24-G1=0
G14·i14+ G24·i24-G1·i1=0
Y6: G2-G25-G15=0
G2·i2-G25·i25-G15·i15=0
Далее представим математическую модель в виде системы уравнений, в которой исключены уравнения энергетического баланса для узлов Y1, Y3, Y5, Y6, т.к. температура на входе и выходе из этих узлов одинакова.
G
12-G11=0
G12·i12-G11·i11=-Q1
G22-G21=0
G22·i22-G21·i21=-Q2
G11-G14-G13=0
G15+G13-G12=0
G15·i15+ G13·i13-G12·i12=0
G21-G24-G23=0
G25+G23-G22=0
G25·i25+ G23·i23-G22·i22=0
G14+G24-G1=0
G2-G25-G15=0
5). Преобразовываем систему уравнений в расчётную матрицу и решаем её методом «обратной матрицы»
В матрице В мощности первого и второго котлов равны и записываются в Мкал/ч:
Qк1=Qк2=2000 кВт= 1680 Мкал/ч;
На рис.6 приведены результаты расчета по данному алгоритму.
6). Внутренний диаметр трубопровода находим по следующей формуле:
,
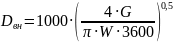мм (13)
где: Dвн – внутренний диаметр трубопровода, мм;
G – расход теплоносителя, т/ч;
W – скорость движения воды в трубопроводе, м/с (принимаем равной 0,5 м/с).
Для определения диаметров использован ГОСТ 10704-91[1]. Результаты расчета представлены в таблице 7.
Таблица 7
Определение диаметров трубопроводов СО и В
Расход |
Значение, м3/ч |
Dвн, мм |
Dн×δ |
G11 |
112,14 |
281,71 |
325,0 х 9,0 |
G12 |
112,14 |
281,71 |
325,0 х 9,0 |
G13 |
40,37 |
169,03 |
177,8 х 4,0 |
G14 |
71,77 |
225,37 |
244,5 х 9,0 |
G15 |
71,77 |
225,37 |
244,5 х 9,0 |
G21 |
112,14 |
281,71 |
325,0 х 9,0 |
G22 |
112,14 |
281,71 |
325,0 х 9,0 |
G23 |
40,37 |
169,03 |
177,8 х 4,0 |
G24 |
67,28 |
218,21 |
244,5 х 9,0 |
G25 |
67,28 |
218,21 |
244,5 х 9,0 |
G1 |
139,05 |
313,70 |
325,0 х 5,5 |
G2 |
139,05 |
313,70 |
325,0 х 5,5 |
Матрица А |
|
|
|
||||||||||||||
G1,1 |
G1,2 |
G1,3 |
G1,4 |
G1,5 |
G2,1 |
G2,2 |
G2,3 |
G2,4 |
G2,5 |
G1 |
G2 |
|
|
R |
|||
-1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
-95,00 |
80,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
-1680 |
|||
1,00 |
0,00 |
-1,00 |
-1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
-1,00 |
1,00 |
0,00 |
1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
-80,00 |
95,00 |
0,00 |
70,00 |
0,00 |
1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-95,00 |
80,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
-1680 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
1,00 |
0,00 |
-1,00 |
-1,00 |
0,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-1,00 |
1,00 |
0,00 |
1,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-80,00 |
95,00 |
0,00 |
70,00 |
0,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
1,00 |
0,00 |
-1,00 |
0,00 |
|
|
0 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
-1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-1,00 |
0,00 |
1,00 |
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Матрица А-1 |
|
|
С |
||||||||||||||
5,33 |
-0,07 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
112,14 |
|||
6,33 |
-0,07 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
112,14 |
|||
2,53 |
-0,03 |
0,00 |
-2,80 |
0,04 |
-0,25 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
40,37 |
|||
2,80 |
-0,04 |
-1,00 |
2,80 |
-0,04 |
0,25 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
71,77 |
|||
3,80 |
-0,04 |
0,00 |
3,80 |
-0,04 |
0,25 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
71,77 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
5,33 |
-0,07 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
112,14 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
6,33 |
-0,07 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
112,14 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
2,53 |
-0,03 |
0,00 |
-2,80 |
0,04 |
0,00 |
0,00 |
|
|
44,86 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
2,80 |
-0,04 |
-1,00 |
2,80 |
-0,04 |
0,00 |
0,00 |
|
|
67,28 |
|||
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
3,80 |
-0,04 |
0,00 |
3,80 |
-0,04 |
0,00 |
0,00 |
|
|
67,28 |
|||
2,80 |
-0,04 |
-1,00 |
2,80 |
-0,04 |
3,05 |
-0,04 |
-1,00 |
2,80 |
-0,04 |
-1,00 |
0,00 |
|
|
139,05 |
|||
3,80 |
-0,04 |
0,00 |
3,80 |
-0,04 |
4,05 |
-0,04 |
0,00 |
3,80 |
-0,04 |
0,00 |
1,00 |
|
|
139,05 |
|||
Рис. 6 – Решение матриц по алгоритму