1. Случайное событие – это событие, которое в данных условиях может произойти, а может не произойти.

Статистическое определение вероятности – определение как предела, к которому стремится относительная частота

Классическое определение – в тех случаях, когда вероятность и относительная частота совпадают:

Применяется только в случаях, когда заранее известно полное число возможных событий и число ожидаемых событий.

Виды комбинированных событий:

- зависимые и независимые;

- совместимые и несовместимые.

Зависимые – на вероятность которых влияет исход какого-либо иного события.

Независимые – появление(непоявление) события А не влияет на вероятность события В.

Несовместные – появление одного события исключает появление других событий в ходе опыта

Совместные – события могут осуществляться в ходе опыта.

2. Теорема сложения вероятностей – вероятность появления какого-либо события из нескольких несовместных событий равна сумме проявления этих событий.

Р(А или В)=Р(А)+Р(В)

Теорема умножения вероятностей – вероятность совместного появления независимых событий равно произведению их вероятностей.

Р(А и В)=Р(А)*Р(В)

Условная вероятность – вероятность события при условии, что другое событие произошло(не произошло). Р(А/В) – Р(А) при условии реализации В.

Тогда: Р(А и В)=Р(А)*Р(В/А).

3. Дискретная случайная величина – случайная величина, у которой совокупность всех ее возможных значений представляет собой счетное множество значений.

Закон распределения дискретных случайных величин – соответствие между всеми возможными значениями этой случайной величины и соответствующими им вероятностями. Чаще всего в виде двустрочной таблицы.

Для дискретной случайной величины – как сумма произведения значения случайной величины на вероятность ее проявления.

4. М – среднее значение величины

- усредненные характеристики степени разброса возможных значений этой величины относительно ее М.

Для непрерывной случайной величины:

М(х)=

Законы распределения непрерывных случайных величин

Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю.

Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х.

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:

.

Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения.

Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям p_i для дискретной случайной величины в непрерывном случае.

Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения:

.

Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью f(x) на определенном участке оси абсцисс.

Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:

Математическое ожидание . Математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.

Дисперсия:

Величина называется поправкой Шеппарда.

Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]:

Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами и (обозначают ), если ее плотность вероятности имеет вид:

где ,

Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при и при ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при : ; ; ). Таким образом, параметр характеризует положение, а параметр - форму кривой плотности вероятности.

5. Закон распространения Бернулли – соответствие между значениями случайной величины и их вероятностями (рассчитанными по формуле Бернулли):

q=1-p – вероятность НЕнаступления.

Случайной величиной, называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.

Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д.

Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т.д.

Биномиальный закон (распределение Бернулли)

В общей форме биномиальный закон описывает осуществление признака в   испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей   белых и   чёрных шаров. Если   — число появления белых шаров в выборке из   шаров, то

где   — вероятность появления при одном извлечении соответственно белого и чёрного,

Производящая функция биномиального распределения задаётся формулой

Основные характеристики биномиального распределения (математическое ожидание и дисперсия):

Математическое ожидание дискретной случайной величины – сумма произведений всех возможных ее значений на вероятности этих значений.

Дисперсией случайной величины наз. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?

Решение. Пусть  . Согласно биномиальному закону и закону сложения имеем

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин M=∑Xi * Pi

Для непрерывных величин M=

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин D=∑(Xi-Xср)² * Рi

Для непрерывных величин D= ² * f(x)dx

Среднеквадратическое отклонение δ=

6. Непрерывные величины принимают бесконечное число возможных значений в каком-либо интервале. Например, время, масса, объем.

Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.

Распределение Пуассона. Если объем серий испытаний n не менее нескольких десятков, а вероятность наступления события в каждом испытании мала, причем наивероятнейшая частота ожидаемого события ( не превышает 10, то часто ограничиваются возможностью получения приближенного значения соответствующей вероятности, которую предоставляет использование формулы Пуассона – «закона редких событий»:

P_n(m)= .

Где m-число ожидаемых событий, Pn(m)-вероятность появления m искомых событий в серии из n независимых испытаний, μ-наивероятнейшая частота ожидаемого события, е-основание натурального логарифма.

Пример: при изготовлении препарата, брак составляет 5%. Найти вероятность того, что среди 100 наугад выбранных упаковок, 3 упаковки будут бракованными.

p=0.05(брак) {0.05<1, p<1}

=100*0.05=5 [

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин

А)Пример: вычислить математическое ожидание случайной величины Х, определяемой как кол-во студентов в наугад выбранной группе, используя табличные данные.

Х	8	9	10	11	12
Р	0,2	0,1	0,3	0,2	0,2

Решение: М= 8*0,2+9*0,1+10*0,3+11*0,2+12*0,2=10,1

Для непрерывных величин

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин D ;

Пример: вычислить дисперсию случайной величины Х, определяемой как кол-во студентов в наугад выбранной группе, используя данные задачи А)

Решение: М( )= ….+ =64*0.2+81*0.1+100*0.3+121*0.2+144*0.2=103.9

D= =103.9-

Для непрерывных величин

Среднеквадратическое отклонение δ=

Пример: найти математ.ожидание, дисперсию и среднее квадратичное отклонение непрерывной случайной величины, заданной плотностью распределения вероятностей f(x), равной ½ на отрезке [1,3] и 0 во всех остальных точках оси абсцисс,т.е. на интервалах (-∞;1); (3,+ )

Решение: М(Х)=

7. Случайная величина (далее СВ) – величина, которая принимает значение в зависимости от стечения случайных обстоятельств. (Пр.: число больных на приеме врача, число студентов в аудитории, номер бочонка, когда его вынимают из мешка, при игре в лото и т.п.)

СВ называется дискретной (далее – ДСВ), если она принимает счетное множество значений. (Пр.: число букв на произвольной странице книге, число волос на голове человека, число молекул в выделенном объеме газа и т.п.)

СВ называется непрерывной (далее – НСВ), если она принимает любые значения внутри некоторого интервала. (Пр.: температура тела, масса зерен в колосьях пшеницы и т.п.)

Вероятность

- предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение)

P(A)=lim_n→∞(m/n)

- отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n)

Плотностью вероятности f(x) непрерывной случайной величины Х называется производная функции распределения F(x) этой величины: f(x)=F’(x)

Основные св-ва плотности распределение вероятностей

1. Плотность вероятности является неотрицательной функцией.

2. Вероятность того,что в результате испытания непрерывная случайная функция примет какое-либо значение из интервала (а,b), равна определенному интегралу от плотности вероятности этой случайной величины. =

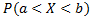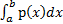
3. Определенный интеграл в пределах от 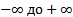от плотности вероятности случайной величины равен 1: 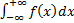=1

4. Определенный интеграл в пределах от от плотности вероятности случайной величины равен функции распределения этой величины: 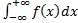=F(x)

Нормальный закон распределения (закон Гаусса). СВ распределена по этому закону, если плотность вероятности имеет вид

a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ.

Дисперсия СВ – МО отклонения случайной величины от ее МО.

D(X)=M[X-M(X)]

Удобная формула: D(X)=M(X²)-[M(X)]²

Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.

По мере возрастания |х-а| функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением σ кривая становится все более и более островершинной. Изменение а при постоянной σ не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенной под кривой, согласно условию нормировки, равна единице. На рисунке изображены три кривые. Для кривых 1 и 2 а=0, но отличаются значением σ (σ₁<σ₂), кривая 3 имеет а≠0, σ=σ_2.

Вычислим функцию распределения.

Обычно используют иное выражение. Введем новую переменную t=(x-a)/σ. Следовательно, dx=σdt. Подставляем это в формулу.

Значение функции Ф(t) обычно находят в составных таблицах, так как интеграл через элементарные функции не выражается. График:

Случайная величина при нормальном распределении может находится в интервале (х₁, х₂). Вероятность этого равна

Р(х₁<x<х₂)=Ф((х₂-а)/σ)-Ф((х₁-а)/σ)

Допустим, что произвольно из нормальных распределений выбираются группы по n значений СВ. Для каждой группы можно найти средние значения (х₁, х₂, х_i). Они сами образуют нормальное распределение (только среднему значению будет соответствовать не вероятность, а относительная частота). МО будет соответствовать исходному, дисперсия и среднее квадратическое отклонение – отличаться в n и в √n соответственно.

D_n=D/n и σ_n=σ/√n.

На рисунке представлены графики нормальных распределений, полученных для групп со значением n, равными 1, 4, 16 и n→∞. При n=1 – исходное распределение, σ_n=σ. При n→∞ σ_n→0, фактически «группа СВ» - все исходное распределение, среднее значение выражается одним числом и соответствует МО, к которому сводится все распределение.

. 8.Стандартное нормальное распределение

Для непрерывных случ.величин описывается законом Гаусса. Распределение вероятностей, которое задается функцией плотности распределения:

где μ —математическое ожидание

σ² — дисперсия.

σ – среднее квадратич. отклонение этой величины

График симметричен относительно вертик.прямой Хmax = μ.

Подставив выражение закона Гаусса в формулу( = )(р –плотность) получим вероятность того, что в результате испытания нормально распределенная случайная величина примет значение из некоторого интервала (а,b).

Р(a<X<b)=

Для нормального закона вычислены некоторые заранее обговоренные стандартные интервалы

1. М- σ 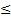х М+ σ (α = 68%)

2. М- 2σ х М+ 2σ (α = 95%)

3. М- 3σ х М+ 3σ (α = 99,7%)

Доверительная вероятность α – вероятность попадания истинного значения в доверительный интервал.

Доверительный интервал – интервал значений случайной величины, в которой с известной вероятностью попадает истинное значение случайной величины.

9. Генеральная совокупность- совокупность, из которой отбирается часть членов для совместного изучения.

Выборка – отобранная для изучения часть элементов генеральной совокупности.

Объем выборки может быть большим или малым, но содержит не менее 3 единиц.

Основное требование, предъявляющее выборки, сводится к получению наиболее полной информации о состоянии генеральной совокупности, из которой взята выборка. Чтобы выборка наиболее полно отображала структуру генеральной совокупности необходимо, чтобы она была репрезентативной, т.е. представительной. Пример: опрос на выборах.

Репрезентативность достигается методом случайного отбора.

Характеристики выборки:

1. Выборочная средняя – определяется как среднее арифметическое значение вариант статического ряда

2. Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения

3. Выборочное среднее квадратическое отклонение – квадратный корень из выборочной дисперсии

Статистическим распределением выборки называют перечень вариантов и соответствующих им частот или относительных частот.

Пример 2. Задано распределение частот выборки объема n = 20:

Таблица 1

xi	2	6	12
ni	3	10	7

Написать распределение относительных частот.

Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:

W₁ = 3/20 = 0,15; W₂ = 10/20 = 0,50; W₃ = 7/20 = 0,35.

Напишем распределение относительных частот:

Таблица 2

xi	2	6	12
wi	0,15	0,50	0,35

Вариационный ряд— последовательность значений заданной выборки .

Графики вариационных рядов:

1. Полигон частот – при построении графика без интервального вариационного ряда по оси абсцисс откладывают срединные значения классов; по оси ординат – частоты.

Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (х1р1);(х2р2);…;(хnpn)

2. Гистограмма – интервальный график. При его построении интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов; по оси ординат – частоты интервалов.

3. Кумулятор – S-образная кривая. По оси абсцисс откладывают значение класса; по оси ординат – накопленные частоты.

10. Благодаря выборочным характеристикам распределения – среднее выборочное, выборочная дисперсия и выборочное среднее квадратичное отклонение, можно оценить соответствующие числовые характеристики генеральной совокупности, причем различают так называемые точечные и интервальные оценки этих характеристик.

Оценка характеристики распределения называется точечной, если она определяется одним числом, которому приближенно равна оцениваемая характеристика.

Генеральная средняя определяется следующим образом.

Генеральной средней дискретной генеральной совокупности наз. среднее арифметическое всех значений изучаемого признака Х в генеральной совокупности:

=(1/N где N-объем совокупности

Вместе с тем наилучшей оценкой генеральной средней является средняя выборочная :

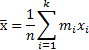
Где mi-частота встречаемости значения xi в выборке, к-кол-во различающихся между собой значений признака, n-объем выборки.

Средняя выборочная представляет собой наилучшую оценку генеральной средней, т.е.

Генеральной дисперсией называется среднее арифметическое квадратов отклонения всех значений изучаемого признака Х в генеральной совокупности от генеральной средней:

Наилучшей оценкой является исправленная выборочная дисперсия ( математическое выражение этого факта: ):

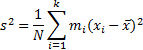
Генеральным средне квадратическим отклонением называется квадратный корень из генеральной дисперсии:

Наилучшей оценкой является исправленное выборочное средне квадратическое отклонение s( математическое выражение этого факта: ):

s=

Интервальной оценкой числовой характеристики наз. оценка, определяемая двумя числами, а именно границами интервала, содержащего оцениваемую характеристику.

Доверительная вероятность α – вероятность попадания истинного значения в доверительный интервал.

Доверительный интервал – интервал значений случайной величины, в которой с известной вероятностью попадает истинное значение случайной величины.

Метод нахождения доверительного интервала на заданной доверительной вероятности. Используется распределение Стьюдента для случайной величины:

Где знаменатель – исправленное среднее квадратичное отклонение средней выборочной.

Полуширину доверительного интервала заданной доверительной вероятности находят:

- коэффициент Стьюдента

Интервальная оценка генеральной средней представляется интервалом

( в котором с доверительной вероятностью находится генеральная средняя.

11. Графические характеристики случайных величин.

Графики вариационных рядов:

1.Полигон частот – при построении графика без интервального вариационного ряда по оси абсцисс откладывают срединные значения классов; по оси ординат – частоты.

Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (х1р1);(х2р2);…;(хnpn)

2.Гистограмма – интервальный график. При его построении интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов; по оси ординат – частоты интервалов.

3.Кумулятор – S-образная кривая. По оси абсцисс откладывают значение класса; по оси ординат – накопленные частоты.

Гистограмма, столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Г. представляет собой совокупность смежных прямоугольников, построенных на прямой линии. Площадь каждого прямоугольника пропорциональна частоте нахождения данной величины в изучаемой совокупности. Пусть, например, измерение диаметров стволов 624 сосен дало следующие результаты:

Диаметр, см

14—22

22—30

30—38

38—62

Число стволов

57

232

212

123

На горизонтальной оси откладываются границы групп, на которые стволы разбиты по их диаметру, и на отрезке, соответствующем каждой группе, строится как на основании прямоугольник с площадью, пропорциональной числу стволов, попавших в данную группу.

Наиболее распространенными характеристиками статистического распространения являются средние величины: мода(мо), медиана(ме) и выборочная средняя.

Мо – равна варианте, которой соответствует наибольшая частота.

Ме – равна варианте, которая расположена в середине статистического распределения.

Выборочная средняя – определяется как среднее арифметическое значение вариант статического ряда:

Пример: таблица масс новорожденных мальчиков и частоты

2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4
1	2	3	7	8	12	13	10	7	6	5	6	6	5	3	3	2	1

то, что в таблице, что не видно-3,4-10; 3,5-7;3,6-6;3,7-5; 3,8-6; 3,9-6;4,0-5,4,1-3;4,2-3;4,3-2;4,4-1

Тогда Мо=3,3(кг); Ме=3,4(кг);

12) Прямые и косвенные измерений. Погрешности измерений. Абсолютная и относительная погрешности измерений. Систематическая, приборная, грубая, случайная погрешности. Примеры. Основной задачей физического эксперимента является измерение численных значений наблюдаемых физических величин. Измерением называется операция сравнения величины исследуемого объекта с величиной единичного объекта.

Принято различать прямые и косвенные измерения. При прямом измерении производится непосредственное сравнение величины измеряемого объекта с величиной единичного объекта. В результате искомая величина находится прямо по показаниям измерительного прибора, например, сила тока - по отклонению стрелки амперметра, вес - по растяжению пружинных весов и т.д. Однако гораздо чаще измерения проводят косвенно, например, площадь прямоугольника определяют по измерению длин его сторон, электрическое сопротивление - по измерениям силы тока и напряжения и т.д. Во всех этих случаях искомое значение измеряемой величины получается путем соответствующих расчетов.

Результат всякого измерения всегда содержит некоторую погрешность. Поэтому в задачу измерений входит не только нахождение самой величины, но также и оценка допущенной при измерении погрешности. Абсолютной погрешностью приближенного числа называется разность между этим числом и его точным значением, причем ни точное значение, ни абсолютная погрешность принципиально неизвестны и подлежат оценке по результатам измерений. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к самому этому числу. Если оценка погрешности результата физического измерения не сделана, то можно считать, что измеряемая величина вообще неизвестна, поскольку погрешность может, вообще говоря, быть того же порядка, что и сама измеряемая величина или даже больше.

Погрешности физических измерений принято подразделять на систематические, случайные и грубые. Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематические погрешности скрыты в неточности самого инструмента и неучтенных факторах при разработке метода измерений. Обычно величина систематической погрешности прибора указывается в его техническом паспорте. Хотя суммарная систематическая погрешность во всех измерениях, проводимых в рамках данного эксперимента, будет приводить всегда либо к увеличению, либо к уменьшению правильного результата, знак этой погрешности неизвестен.

Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Они имеют различные значения даже для измерений, выполненных одинаковым образом, то есть носят случайный характер. Допустим, что сделано n повторных измерений одной и той же величины. Если они выполнены одним и тем же методом, в одинаковых условиях и с одинаковой степенью тщательности, то такие измерения называются равноточными.

Третий тип погрешностей, с которыми приходится иметь дело - грубые погрешности или промахи. Под грубой погрешностью измерения понимается погрешность, существенно превышающая ожидаемую при данных условиях. Она может быть сделана вследствие неправильного применения прибора, неверной записи показаний прибора, ошибочно прочитанного отсчета, неучета множителя шкалы и т.п.

13) Методы оценки приборной и случайной погрешностей. Коэффициент Стьюдента. Методы оценки косвенных измерений. Примеры. Вычисление погрешностей. В дальнейшем будем предполагать, что

1) грубые погрешности исключены;

2) поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты;

3) все систематические погрешности известны (с точностью до знака).

В этом случае результаты измерений оказываются все же не свободными от случайных погрешностей. Если случайная погрешность окажется меньше систематической, то, очевидно, нет смысла пытаться уменьшить величину случайной погрешности - все равно результаты измерений не станут значительно лучше и, желая получить большую точность, нужно искать пути к уменьшению систематической погрешности. Наоборот, если случайная погрешность больше систематической, то именно случайную погрешность нужно уменьшить в первую очередь и добиться того, чтобы случайная погрешность стала меньше систематической, с тем чтобы последняя опять определяла окончательную погрешность результата. На практике обычно уменьшают случайную погрешность до тех пор, пока она не станет сравнимой по величине с систематической погрешностью. Как будет видно из дальнейшего, случайная погрешность уменьшается при увеличении числа измерений.

Поскольку из-за наличия случайных погрешностей результаты измерений по своей природе представляют собой тоже случайные величины, истинного значения x ист измеряемой величины указать нельзя. Однако можно установить некоторый интервал значений измеряемой величины вблизи полученного в результате измерений значения xизм, в котором с определенной вероятностью содержится x ист. Тогда результат измерений можно представить в следующем виде: (2)

где D x - погрешность измерений. Вследствие случайного характера погрешности точно определить ее величину невозможно. В противном случае найденную погрешность можно было бы ввести в результат измерения в качестве поправки и получить истинное значение xист.. Задача наилучшей оценки значения xист и определения пределов интервала (2) по результатам измерений является предметом математической статистики.

Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности s (ее часто называют стандартной погрешностью или стандартом измерений).

Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью xист попадает в этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительно величины xист. Если ограничиться учетом только случайных погрешностей, то при небольшом числе измерений n для уровня доверительной вероятности a полуширина доверительного интервала (2) равна

где ta,n - коэффициент Стьюдента

коэффициенты Стьюдента— числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.