2.4. Частотные характеристики типовых звеньев направленного действия.

2.4.1. Дифференцирующее и интегрирующее звенья.

Комплексные частотные передаточные функции дифференцирующего и интегрирующего звеньев в соответствии с их передаточными функциями имеют следующий вид:

– дифференцирующее звено: ;

– интегрирующее звено: .

Н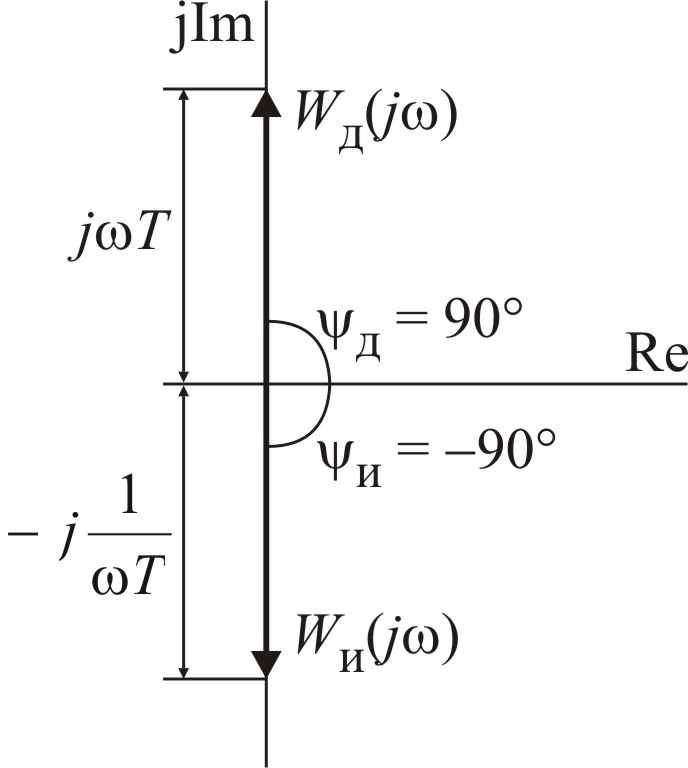 а комплексной плоскости вектор частотной функции дифференцирующего звена расположен на положительной части мнимой оси, вектор частотной функции интегрирующего звена – на отрицательной части.

Фазы векторов частотных функций звеньев не зависят от частоты и составляют: для дифференцирующего звена ψ_д = 90º, для интегрирующего звена ψ_д = 90º.

Амплитудно-фазовая характеристика дифференцирующего звена с увеличением частоты неограниченно возрастает в положительной части мнимой оси, АФХ интегрирующего звена – стремится к нулю в отрицательной части мнимой оси.

Л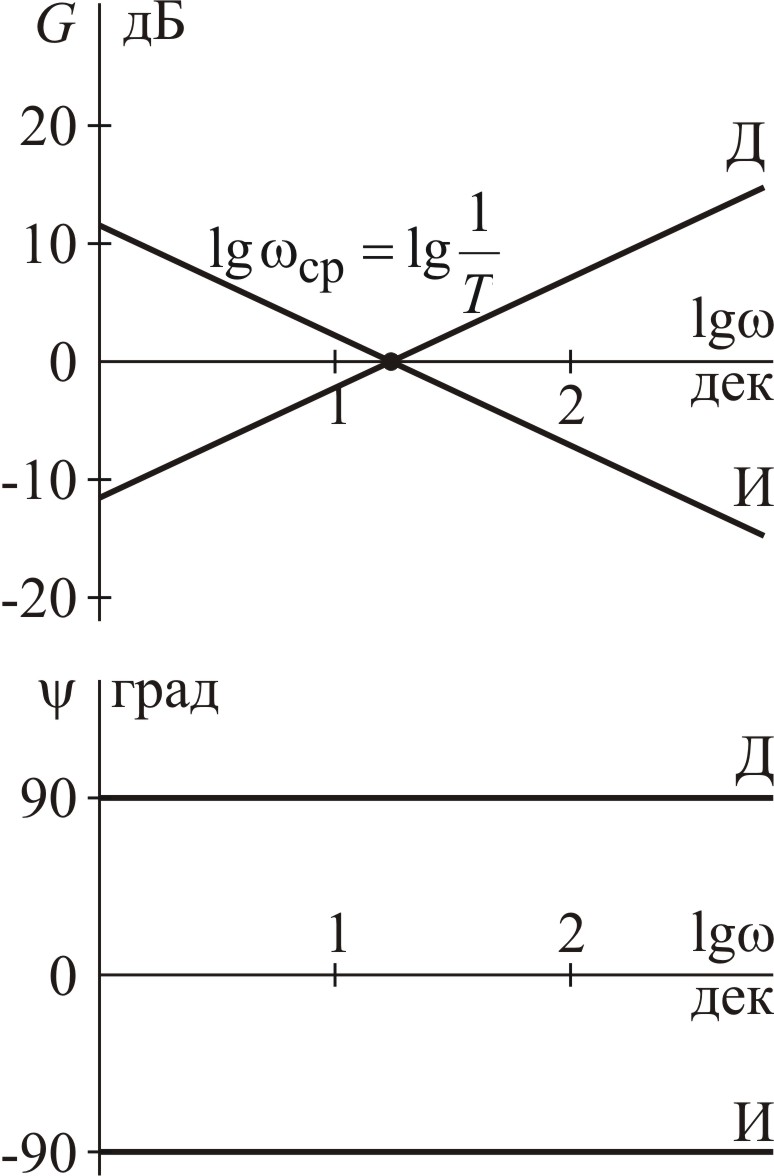 огарифмические амплитудно-частотные характеристики звеньев определяются выражением

.

Знак "+" в формуле соответствует дифференцирующему звену, знак "–" – интегрирующему звену. Обе характеристики линейны и имеют наклон крутизной ±20 дБ/дек.

Для определения расположения характеристик в координатных осях запишем выражение, приведенное выше, отдельно для дифференцирующего и интегрирующего звеньев, в следующем виде:

;

.

Таким образом, каждая из характеристик состоит из переменной части ±20lgω, идущей из начала координат с наклоном + или – 20 дБ/дек и постоянной части смещающей характеристику вдоль оси ординат. Частота среза определяется следующим выражением:

.

При решении практических задач для построения ЛАЧХ дифференцирующего или интегрирующего звена вычисляется логарифм частоты среза, на оси абсцисс откладывается величина lgω_ср и через эту точку проводится прямая линия с наклоном +20 дБ/дек для дифференцирующего звена и –20 дБ/дек для интегрирующего звена.

Логарифмические фазо-частотные характеристики звеньев – это прямые, параллельные оси абсцисс, расположенные на уровне +90º для дифференцирующего звена и –90º для интегрирующего звена.

2.4.2. Форсирующее и апериодическое звенья первого порядка.

Комплексная частотная функция форсирующего звена имеет вид:

W_ф(jω) = K(1+jωT);

апериодического звена первого порядка:

.

Модуль вектора частотной функции форсирующего звена определяется следующим выражением:

;

апериодического звена 1-го порядка:

.

Фазы векторов частотных функций звеньев определяются выражением:

(ω) = ±arctg(ωT).

Знак "+" в формуле относится к форсирующему звену, знак "–" – к апериодическому звену.

Амплитудно-фазовая характеристика форсирующего звена представляет собой на комплексной плоскости прямую, параллельную мнимой оси и отстоящую от нее на расстоянии, равном коэффициенту усиления звена. С увеличением частоты вектор частотной функции форсирующего звена неограниченно возрастает, поэтому его АФХ также неограниченно растет, при этом фаза вектора приближается к углу 90⁰.

А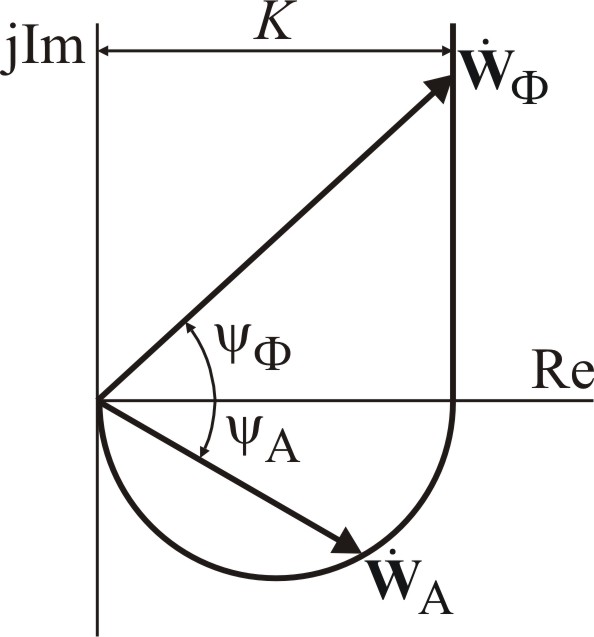 мплитудно-фазовая характеристика апериодического звена, представляет собой полуокружность диаметром, равным коэффициенту усиления звена.

Логарифмические амплитудно-частотные характеристики форсирующего и апериодического звеньев определяются логарифмированием модулей частотных функций:

.

Знак "+" в формуле относится к форсирующему звену, знак "–" – к апериодическому звену.

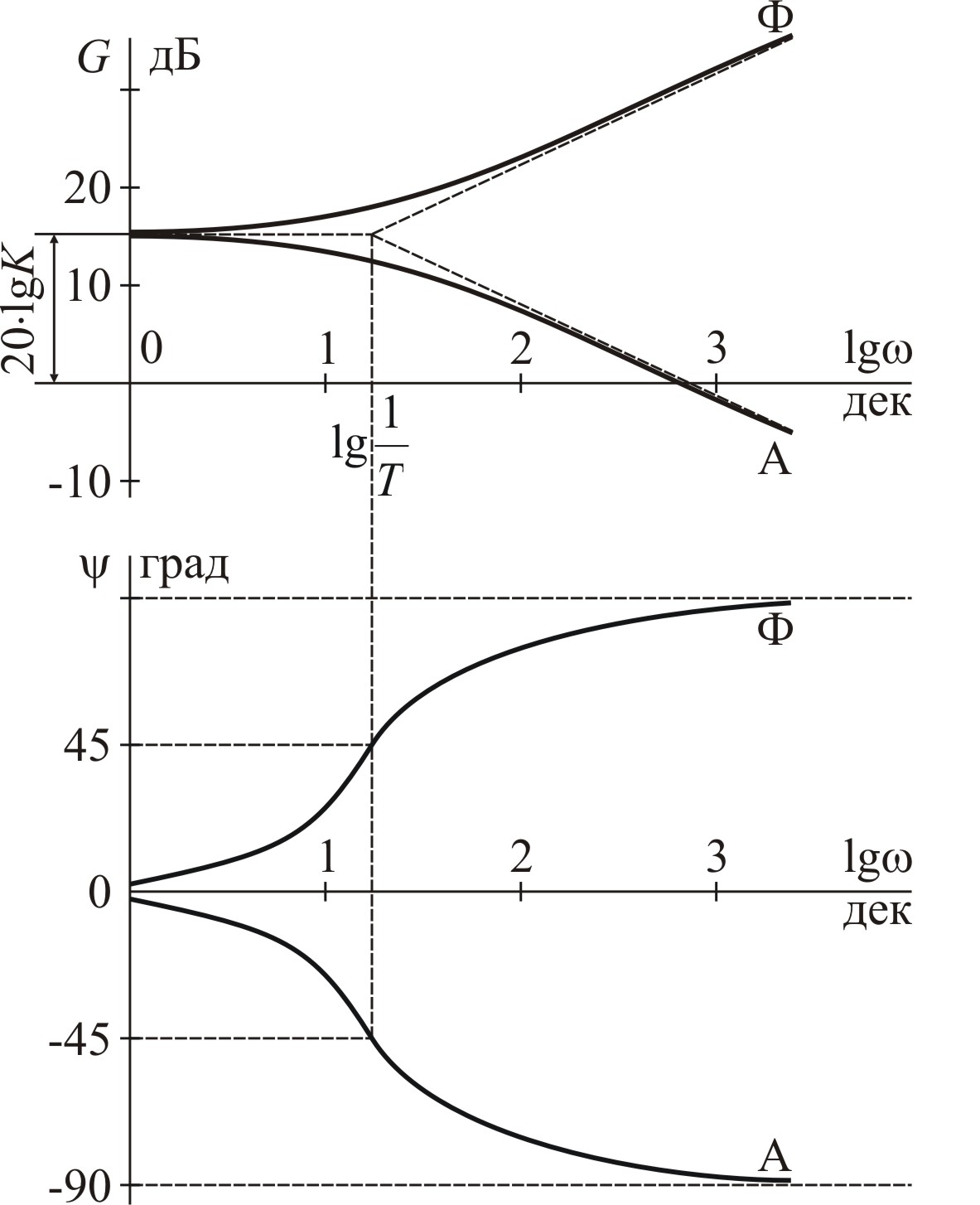
Для рассматриваемых звеньев, во избежание громоздких вычислений, можно использовать упрощенные ЛАЧХ, составленные из двух линейных отрезков. Горизонтальный отрезок располагают на уровне 20lgK. Аналитические выражения для наклонных отрезков могут быть получены из второго слагаемого формулы ЛАЧХ, если пренебречь единицей под знаком корня:

.

Эти выражения соответствуют формулам ЛАЧХ дифференцирующего и интегрирующего звеньев. Наклонные отрезки имеют крутизну наклона ±20 дБ/дек и сопрягаются с горизонтальными отрезками характеристики при частоте . Частоту _с называют частотой сопряжения.

Наибольшая погрешность линеаризации ЛАЧХ форсирующего и апериодических звеньев имеет место при частоте сопряжения и составляет 20lg  = 3 дБ. Графики упрощенных линеаризованных ЛАЧХ показаны на рисунке штриховыми линиями.

При решении практических задач для построения линеаризованной ЛАЧХ вычисляются координаты точки сопряжения горизонтальной и наклонной частей характеристики: . Влево от этой точки проводится горизонтальный отрезок; вправо – наклонный. Наклон отрезка составляет 20 дБ/дек для форсирующего звена и –20 дБ/дек для апериодического.

Логарифмические фазо-частотные характеристики форсирующего и апериодического звеньев описываются функциями арктангенса и расположены симметрично относительно оси абсцисс. При частоте сопряжения фазовый угол характеристик составляет ±45.

При решении практических задач ЛФЧХ строят по шаблону. Шаблон ЛФЧХ совмещается фазой 45 для форсирующего и –45 для апериодического звеньев с логарифмической частотой сопряжения звена lgω_с по оси абсцисс.