1.4. Оценка качества регулирования по корням характеристического уравнения.

Методы, основанные на расчетах переходного процесса в системе автоматического управления и оценку качества регулирования непосредственно по виду переходного процесса, называют прямыми методами анализа качества.

В инженерной практике используют косвенные методы анализа, не требующие решения системы дифференциальных уравнений. Анализируя слагаемые свободной составляющей y_св(t) процесса регулирования можно установить связь основных показателей качества с корнями характеристического уравнения системы.

Математическое выражение свободной составляющей переходного процесса устойчивой системы с вещественными корнями характеристического уравнения p₁=-α₁, p₂=-α₂, …, p_n=-α_n есть сумма экспоненциальных функций:

.

Поэтому можно считать временем процесса регулирования t_р длительность затухания экспоненциальной функции с наименьшим по модулю показателем степени, то есть соответствующей наименьшему по модулю вещественному корню характеристического уравнения.

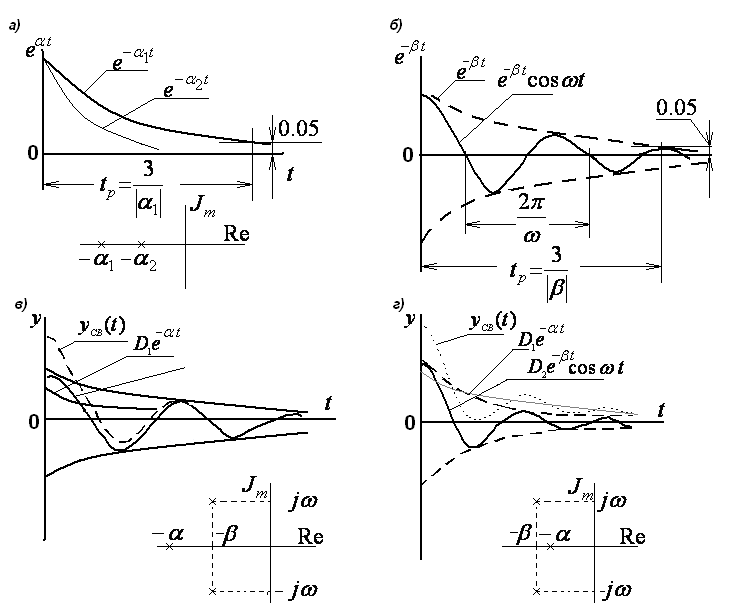
Время процесса регулирования t_р, равное времени затухания экспоненциальной функции определяется следующей формулой:

.

При наличии комплексных сопряженных корней следует ожидать в соответствии с выражением колебательный характер процесса. Степень колебательности μ зависит от соотношения мнимой части ω корней, характеризующей частоту собственных колебаний и вещественной части β, характеризующей длительность затухания колебательной функции.

Степень колебательности равна удвоенному числу колебаний за время затухания:

,

период колебаний равен , отсюда степень колебательности:

.

Характер процесса регулирования зависит от соотношения модуля вещественной части комплексных корней |β| и наименьшего модуля вещественных корней |α|_min. Если |α|_min>|β|, то характер процесса будет колебательным, а время затухания переходного процесса определится выражением , если же наоборот |α|_min<|β|, то характер процесса будет монотонно – колебательным, а время регулирования определится выражением .

2. Частотные характеристики динамических звеньев и систем автоматического управления.

2.1. Комплексная частотная передаточная функция.

В основу методов исследования и расчета систем автоматического управления положены частотные характеристики звеньев направленного действия. Частотные характеристики показывают, как изменяются амплитуда и фаза выходного гармонического сигнала звена направленного действия относительно входного в зависимости от частоты этого сигнала. Частотные характеристики могут рассматриваться не только для простейших звеньев, но и сложных функциональных элементов или САУ в целом.

Рассматривается передача линейным звеном направленного действия гармонического сигнала x(ωt) c амплитудой А_x, угловой частотой ω, начальной фазой θ_x:

.

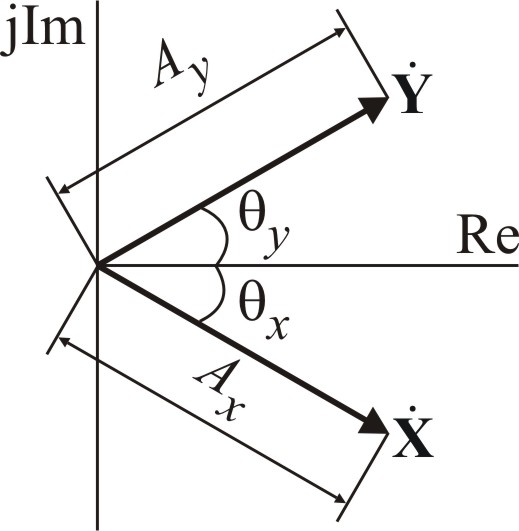
На выходе звена в установившемся режиме гармонический сигнал y(ωt) имеет ту же частоту, но изменившиеся амплитуду А_y и фазу θ_y:

.

Изменения гармонического сигнала при передаче его звеном можно характеризовать отношением амплитуд и разностью фаз ψ = θ_у–θ_х.

Если угловую частоту гармонического сигнала изменять в широком диапазоне, можно получить зависимость относительного изменения амплитуды А(ω) и фазы ψ(ω) сигнала при передаче его звеном, функциональным элементом или системой. Такие зависимости называют амплитудно-частотными (АЧХ) и фазо-частотными (ФЧХ) характеристиками.

Гармонические сигналы x(ωt) и y(ωt) можно представить на комплексной плоскости в виде векторов , , вращающихся с угловой частотой ω. Модуль каждого вектора равен амплитуде соответствующего сигнала, а их положение на комплексной плоскости определяется начальными фазами. Векторы этих сигналов в комплексной форме имеют следующее выражение:

;

.

Комплексной частотной функцией (комплексным коэффициентом передачи) называют отношение вектора выходного гармонического сигнала к вектору входного сигнала :

.

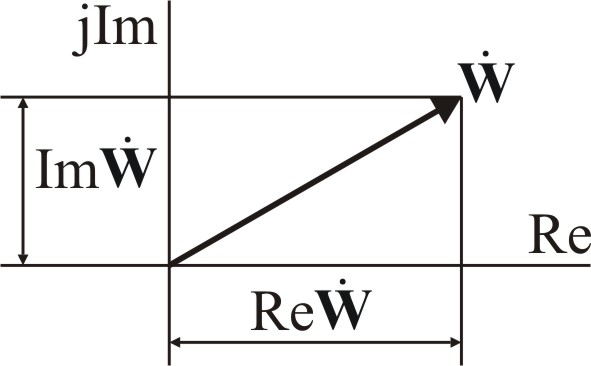
Таким образом, комплексная частотная передаточная функция характеризует относительное изменение амплитуды А и фазы ψ гармонического сигнала при передаче его звеном или системой. На комплексной плоскости частотную передаточную функцию можно представить вектором :

.

Модуль вектора есть отношение амплитуд, а фаза вектора ψ = θ_y – θ_x – разность фаз входного и выходного гармонических сигналов.

При анализе частотных характеристик более удобной является алгебраическая форма записи комплексной частотной функции с выделением вещественной Re W(j) и мнимой Im W(j) частей:

.

При обратном преобразовании для определения модуля и фазы вектора комплексной частотной функции используют известные соотношения:

;

.