1. Устойчивость и качество регулирования систем автоматического управления.

1.1. Устойчивость систем автоматического управления.

В системах автоматического управления под влиянием возмущающих или управляющих воздействий возникают процессы перехода из одного состояния в другое. Характер переходных процессов зависит от динамических свойств звеньев, составляющих систему. Если по окончании этих процессов выходная переменная системы приходит в равновесное состояние, то такая система устойчива. Различают статическую и динамическую устойчивость.

Статическая устойчивость характеризуется созданием системой автоматического управления факторов и условий, противодействующих изменениям выходной переменной, вызванным возмущающими воздействиями. Основным признаком обеспечения статической устойчивости является отсутствие положительных обратных связей в системе, т.е. все обратные связи должны быть отрицательными.

Динамическая устойчивость системы автоматического управления связана с проявлением инерционности функциональных элементов системы при передаче ими сигналов. Обеспечение динамической устойчивости достигается соответствием величины общего коэффициента усиления системы K₀ по контуру главной обратной связи с соотношением существенных постоянных времени апериодических звеньев, входящих в этот контур.

Устойчивость линейных систем не зависит от величины возмущающего воздействия. Система, устойчивая при малых воздействиях, будет устойчива при больших воздействиях. Для оценки устойчивости линейной системы достаточно исследовать ее устойчивость по дифференциальным уравнениям, характеризующим движение системы.

Процессы, происходящие в большой части реальных систем характеризуются нелинейными уравнениями, которые могут быть для упрощения линеаризованы. В этом случае исследование реальной системы будет заменено исследованием линеаризованной системы. Правильность суждения об устойчивости нелинейной системы по линеаризованным уравнениям доказана А.М.Ляпуновым.

Аналитическая формулировка условия устойчивости сводится к тому, что возникающее в результате нарушения равновесия отклонение выходной переменной ∆y от заданного уровня по истечении достаточного промежутка времени должно стать меньше некоторого заранее заданного значения ε:

lim|∆y (t) |≤ε , при t→∞.

Если выходная переменная после окончания изменения нерегулируемого воздействия возрастает или совершает колебания с постоянной или возрастающей амплитудой, то система считается неустойчивой, так как она не проходит в установившееся состояние.

Для аналитического исследования устойчивости надо рассмотреть общее дифференциальное уравнение системы автоматического управления и проанализировать его решение:

.

Общее дифференциальное уравнение может, получено из системы дифференциальных уравнений динамических звеньев; входящих в замкнутый контур САУ. Приведение системы дифференциальных уравнений к общему уравнению можно выполнить методом подстановки или путем матричных преобразований.

Левая часть уравнения характеризует изменение выходной переменной и ее производных, правая часть представляет собой возмущающее воздействие. Аналитическое решение уравнения можно представить в виде суммы двух составляющих - вынужденной и свободной:

.

Вынужденная составляющая является частным решением, определяемым правой часть уравнения (5.1), то есть внешним возмущающим воздействием на систему. Свободная составляющая является общим решением однородного линейного дифференциального уравнения системы и определяется его левой частью:

.

Здесь D₁ ,D₂ … D_n постоянные интегрирования;

p₁, p₂ … p_n - корни характеристического уравнения, соответствующего общему дифференциальному уравнению:

.

Корни характеристического уравнения определяются только левой частью общего дифференциального уравнения, то есть внутренними параметрами системы, а постоянные интегрирования правой частью, то есть внешними воздействиями на систему.

Динамическая устойчивость системы определяется только характеристическим уравнением общего дифференциального уравнения, то есть параметрами системы, так как в понятие устойчивости системы включается только факт наличия или отсутствия затухания переходного процесса, а не его форма и длительность.

Изменение во времени свободной составляющей y_св(t) зависит от вида корней характеристического уравнения. Если все корни вещественные отрицательные: p₁=-α₁, p₂=-α₂, … , p_n=-α_n, то свободная составляющая представляет собой сумму экспоненциальных, затухающих с течением времени функций вида e^-αt. При наличии хотя бы одного положительного корня соответствующая функция e^+αt в сумме слагаемых свободной составляющей является степенной, то есть возрастающей. В этом случае свободная составляющая y_cв(t) возрастающая, а система неустойчива.

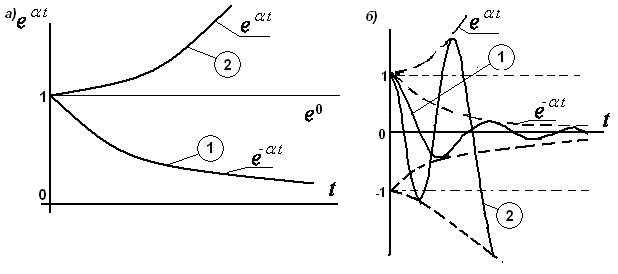
Если один из корней нулевой, то соответствующая функция e^o=1 в сумме слагаемых свободной составляющей незатухающая, а система находится на грани устойчивости.

Если в решении характеристического уравнения имеются комплексные сопряженные корни вида , то соответствующие функции слагаемых свободной составляющей можно привести к следующему виду:

,

где одна из функций правой части выражения является гармонической, а другая экспоненциальной или степной, в зависимости от знака вещественной части корней. Коэффициент амплитуды b и начальная фаза θ гармонической функции в выражении, зависят от соотношения постоянных D₁ и D₂ .

Если вещественная часть β комплексных корней будет отрицательной, гармоническая функция и, следовательно, свободная составляющая выходной переменной будет затухающей, а система устойчивой.

Если вещественная часть β комплексных корней будет положительной, то гармоническая функция будет возрастающей, следовательно, система будет неустойчивой.

При мнимых корнях гармоническая функция будет незатухающей, а система находится на грани устойчивости.

Условия устойчивости линейных систем, определяемые первой теоремой А.М.Ляпунова:

1. Система устойчива, если все корни характеристического уравнения имеют отрицательные вещественные части.

2. Система неустойчива, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть.

3. Система находится на грани апериодической устойчивости, если характеристическое уравнение имеет один нулевой корень.

4. В том случае, когда характеристическое уравнение содержит пару мнимых корней – система находится на грани колебательной устойчивости.

Устойчивость линеаризованной системы полностью определяет устойчивость исходной нелинейной системы. Если линеаризованная система находится на грани устойчивости, то для оценки ее работоспособности требуются дополнительные исследования.

Метод оценки устойчивости системы по корням характеристического уравнения не позволяет в случае неудовлетворительного результата установить основные факторы, воздействуя на которые можно повысить устойчивость исследуемой системы. В этом случае целесообразно использовать другие математические условия устойчивости, называемые критериями устойчивости.