§9 Случайные погрешности

Случайные погрешности возникают вследствие одновременного воздействия на объект измерения нескольких независимых величин, измерения некоторых носят флуктуационный характер. Абсолютное значение и знак этих погрешностей подчиняются вероятностным законам.

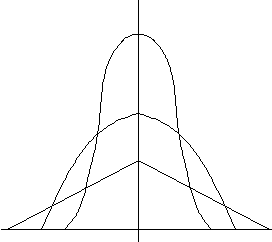
Рис. 4 Стандартные аппроксимации некоторых законов распределения плотности вероятности

Последним двум б и в соответствующим равномерному и треугольному закону распределения подчиняются погрешности, возникающие при дискретизации непрерывных величин. Примерами погрешностей имеющих равномерное распределение могут служить погрешности обусловленные трением в опорах электромеханических измерительных устройствах, а так же при отсчете показаний по равномерной шкале стрелочного прибора. Треугольный закон встречается у цифровых приборах. При обработке результатов измерений непрерывных физических величин чаще используют нормальный закон Гаусса (рис 5.а), который записывается в виде:

(*)

где

-значение случайной погрешности

-среднеквадратическое отклонение ряда измерений

- число измерений

- плотность вероятности для определения значения

(*) описывают ассиметричную кривую

1 2> 1 > 3> 2 >

Рис.5 График функции (*) при различных значениях

Анализируя выражение (*) можно сделать ряд выводов:

1. Т.к. входит в показатель степени , то её значения одинаковые по абсолютной величине, но различны по знаку.

2. Чем меньше , тем больше у, т.е. малым значениям соответствует большая вероятность их появления и наоборот.

Характер кривых на рисунке (г) зависит от значений . Чем меньше , тем чаще наблюдаются малые случайные погрешности, следовательно, тем выше точность измерения. При больших значениях большие случайные погрешности встречаются чаще, следовательно, точность меньше.

§10 Погрешность косвенных измерений

При косвенных изменениях измеряемая величина функционально связана с другими величинами , которые подвергаются прямым измерениям.

Абсолютная погрешность измеряемой величины является некоторой функцией погрешности прямых измерений.

В простейшем случаи при одной переменной в результате измерения получаем:

Разложим правую честь в ряд Тейлора и сохраним члены разложения, содержащие в первой степени:

Отсюда абсолютная и относительная погрешности равны:

В общем, случаи, когда , абсолютная погрешность результата косвенных измерений находится как сумма :

где слагаемые являются квадратными частными погрешностей прямых измерений. Аналогично вычисляется и относительная погрешность:

§11 Суммирование погрешностей

Случайная погрешность измерительные устройства, состоящие из m блоков с независимыми случайными погрешностями каждого блока находится путём геометрического суммирование.

(*)

Аналогично определяется относительная погрешность, а так же среднеквадратичное отклонение.

Если на конечный результат измерения погрешности отдельных блоков оказывают разное влияние, то вводятся весовые коэффициенты и формула (*) преобразуется, например, для относительной погрешности:

-весовой коэффициент

Систематическая погрешность суммируется алгебраически с учётом их знаков. Суммарная погрешность является модулем полученной суммы:

При наличии случайной и систематической погрешности, общая погрешность измерения равна их общей систематической сумме: