3) Определим значение перегрева на поверхности х=0 и в любой точке полупространства к концу действия импульса [1]:

(20)

(21)

т.к.

q=P/S=P/(2L₁*2L₂) – тепловой поток, Вт/м². (22)

q =

Рассчитаем перегрев в источника на поверхности (х=0):

Таблица 2 – Расчет перегревов от источника вглубь подложки

Расчеты значений перегрева в таблице 2 проведены в программе MathCad 2001®.

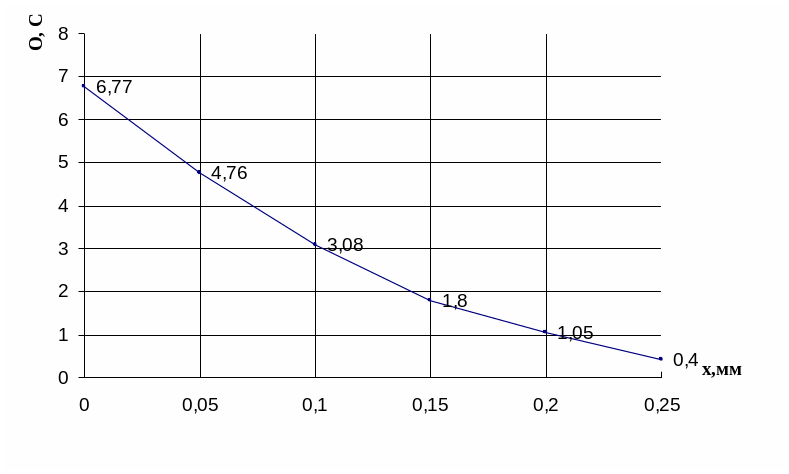
Рисунок 4 – Температурное поле вглубь подложки

(построено при помощи программы Microsoft® Excel 2002)

3) Расчет перегревов от источника на поверхности подложки.

Определим значение вспомогательной функции u [1]:

, (23)

• Перегрев в точке у на поверхности (z=0) источника θ₀, ºС [1]:

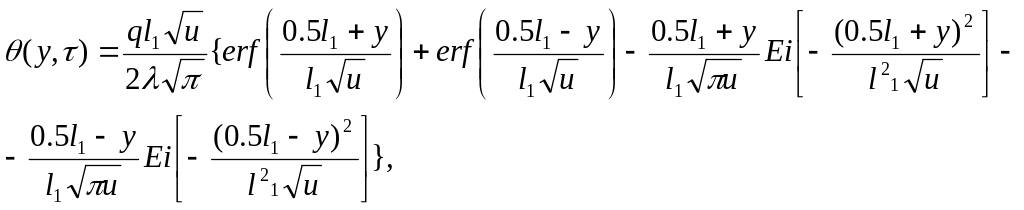(24)

где erf n – функция ошибок Гаусса [3];

Ei – интегральная показательная функция [1],

Определим значение перегрева на поверхности у=0:

Таблица 3 – Расчет перегревов от источника на поверхности подложки

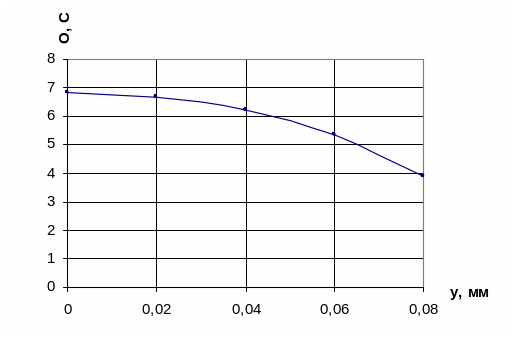
Рисунок 5 – Температурное поле на поверхности подложки

(построено при помощи программы Microsoft® Excel 2002)

3 Задача №3

3.1 Условие задачи

В центральной части микроплаты ( подложки ) МЭУ размерами L₁ х L₂ х h_П находятся три одинаковых элемента квадратной формы ( сторона а), центры которых образуют равносторонний треугольник со стороной b. Каждый из элементов рассеивает тепловую мощность Р. Рассчитайте перегревы элементов в характерных точках, при условии что микроплата обладает коэффициентом теплопроводности λ_П и крепится к корпусу МЭУ с помощью клея толщиной h_К и коэффициентом теплопроводности λ_К.

3.2 Исходные данные

L₁ х L₂, мм = 34х20

h_П, мм = 0,75

Р, Вт = 1,5

а, мм = 2

λ _П , Вт/м ∙ К = 10

b, мм =10

h_К ,мм = 0,1

λ _К , Вт/м ∙ К = 1

3.3 Решение

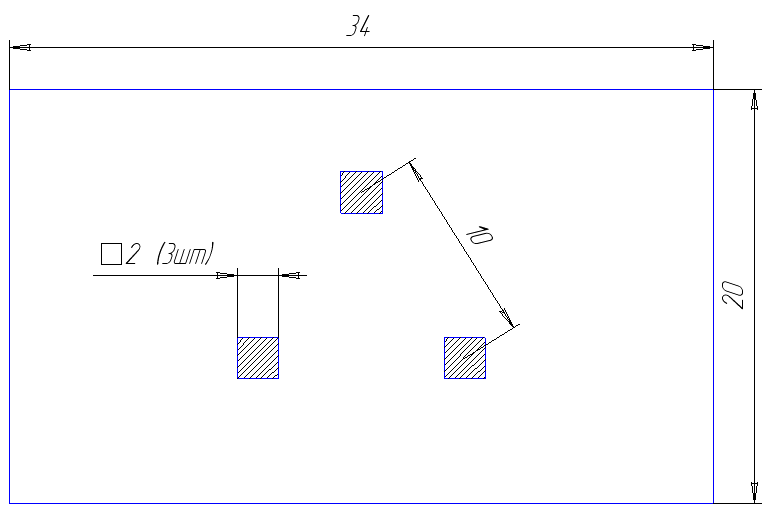
Рисунок 6 – Расположение элементов на микроплате.

Вводим допущения:

1. Корпус МЭУ герметичен;

2. Влиянием размеров подложки на температурное поле каждого источника можно пренебречь;

3. Подложка изготовлена из изотропного материала.

Определяем зону влияния каждого источника выделения тепла а, мм [2]:

(25)

где - толщина изотопной модели, м [2]; (26)

h_п – толщина подложки, м;

h_к – толщина слоя клея между подложкой и основанием корпуса микроплаты, м;

λ_п – коэффициент теплопроводности подложки, Вт/м*К;

λ_п – коэффициент теплопроводности клея, Вт/м*К.

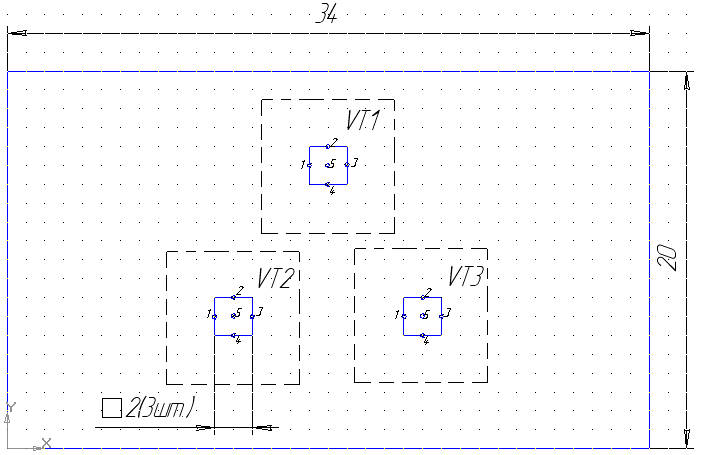
Рисунок 7 –Распределение зон теплового влияния в центральной части микроплаты

(Масштаб 6:1)

ЗТВ не пересекаются, достаточно выполнить расчет перегревов в двух характерных точках источника теплоты: одна в центре и одна на периферии.

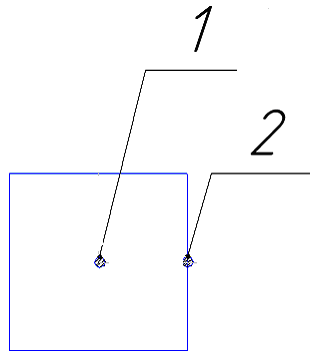
Рисунок 8 – Характерные точки источника теплоты

1-точка в центре;

2-точка на периферии.

Собственный перегрев θ, ºС, на поверхности источника тепла [4]:

(27)

где – тепловое сопротивление пластины, град/Вт; (28)

– поверхностная плотность тепловыделения, Вт/м²; (29)

P – тепловая мощность элемента, Вт;

; (30)

; (31)

; (32)

; (33)

- толщина подложки с учетом клеевого слоя, м; (34)

u, v – постоянные интегрирования;

. (35)

Определим собственный перегрев для точки 5 элемента VT1 (х=0,017; у=0,015):

Определим собственный перегрев для точки 1 элемента VT1(х = 0,016; у=0,015):

Результаты расчетов перегревов всех источников в таблице 4.

Таблица 4 – Результаты расчетов перегревов для всех источников тепла.

3.4 Вывод

Т.к. для всех элементов отсутствуют наведенные перегревы от соседних источников то, полный перегрев принимаем равным собственному.

В результате полный перегрев в характерных точках на поверхности элементов (см. рисунок 8):

-для точки (1) в центре элемента θ1, ºС =36,72

-для точки (2) на периферии элемента θ2, ºС =36,69

Список литературы

1. Дульнев Г.Н., Семяшкин Э.М. Теплообмен в радиоэлектронных аппаратах. Л.: Энергия, 1968. - 360 с.

2. Карачинов В.А. Тепло – и массообмен в РЭА ./ Метод. указ. к курсовой работе.-НПИ, Новгород, 1988. - 33 с.

3. Лыков А.В. Теория теплопроводности. М.:Высшая школа,1967. - 600 с.

4. Роткоп Л.Л., Спокойный Ю.Е. Обеспечение тепловых режимов при конструировании РЭА. – М.:Сов.радио, 1976. – 232с.