17

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Новгородский государственный университет имени Ярослава Мудрого

Институт электронных и информационных систем

Кафедра «Проектирование и технология радиоаппаратуры»

Практическая работа

по дисциплине«Тепло- и массообмен в РЭС»

для направления 551100 «Проектирование и технология электронных средств»

Преподаватель:

______В.А. Карачинов

“____” ________2007 г.

студент гр. 4022

________ С.И. Гребцов

“____” ________2007 г.

3

1.1 Условие задачи

Среднеповерхностная температура корпуса МЭУ Т_S .Размеры корпуса L₁хL₂хH, коэффициент черноты ε , температура окружающей среды Т_С. Рассчитайте мощность, рассеиваемую МЭУ при атмосферном давлении р = 300 ÷ 900 мм.рт.ст. Построить график зависимости Р = f( p ).

1.2 Исходные данные для задачи

L₁ х L₂ х H, мм = 19 х 15 х 5

Т_S , ˚ С = 60

ε = 0,84

Т_С, ˚ С = 10

1.3 Решение

Для решения задачи сформулируем следующие допущения:

• Теплоотдача происходит в условиях естественной конвекции в неограниченном пространстве;

• Все поверхности блока (корпуса) являются изотермическими поверхностями;

• Окружающая среда – воздух.

Примем расположение корпуса радиоэлектронного аппарата согласно рисунку 1.

Рисунок 1 – Ориентация корпуса в пространстве

1. Определим закон движения жидкости около нагретой поверхности [1]:

Если определяющий размер (L, мм) плоской поверхности и ее температурный напор T-T_С удовлетворяют неравенству:

, [град] (1)

то движение жидкости подчиняется закону степени ¼, в противном случае имеет место теплообмен по закону степени 1/3.

Для плоской горизонтальной поверхности L= min{L₁,L₂}; для плоской вертикальной поверхности L= H.

Проверяем соотношение (1) для горизонтальных поверхностей ABCD и EFGK (L=L₂=15):

Неравенство выполняется.

Проверяем соотношение (1) для вертикальных поверхностей AEKD, AEFB, FGCB и KGCD (L=H=5):

Неравенство выполняется.

2. Для расчета конвективного коэффициента теплоотдачи можно применить следующие формулы:

   • Для вертикально ориентированной поверхности высотой Н, м:

, [Вт/м²·град] (2)

• Для горизонтально ориентированной поверхности, обращенной нагретой стороной вверх:

, [Вт/м²·град] (3)

• Для горизонтально ориентированной поверхности, обращенной нагретой стороной вниз:

, [Вт/м²·град] (4)

где А₂ – коэффициент, зависящий от физических параметров среды (значения А₂ для воздуха приведены в таблице 1-5 [1]).

Для определения значения А₂ найдем определяющую температуру Т_m, ºС:

, [град] (5)

Тогда А₂=1,21 для всех поверхностей.

Рассчитываем конвективный коэффициент теплоотдачи α_к, Вт/м²·град [1]:

• Для боковых поверхностей:

• Для верхней горизонтальной поверхности:

• Для нижней горизонтальной поверхности:

3. Найдем площади поверхностей теплообмена S, м²:

(6)

(7)

4. Определим количество тепла, переносимого в единицу времени от МЭУ к жидкости (воздуху) Р, Вт [1]:

(8)

5. Суммарную мощность Р_Σ, Вт, рассеиваемую поверхностью МЭУ в результате конвекции, найдем по формуле [1]:

(9)

6. Рассчитаем мощность, рассеиваемую в результате излучения, Р_л, Вт []:

, (10)

где α_л – коэффициент теплообмена излучением между поверхностью МЭУ и воздухом, Вт/м²·град;

S=S_Σ – полная площадь поверхности МЭУ, м².

Определим коэффициент теплообмена α_л, Вт/м²·град [1]:

, (11)

где i, j – индексы поверхностей, между которыми происходит теплообмен излучением (i – поверхность МЭУ, j – воздух);

ε_пij – приведенная степень черноты системы поверхностей i и j (ε_пij=ε=0,84);

φ_ij – коэффициент облучаемости системы поверхностей i и j (φ_ij=1, т.к. излучение происходит в неограниченное пространство);

f(t_i, t_j) – функция, зависящая от температуры поверхностей (t_i=Т_S, t_j=T_C), Вт/м²·град .

Значение функции f(T_S, T_C)= f(60, 10) находим по формуле:

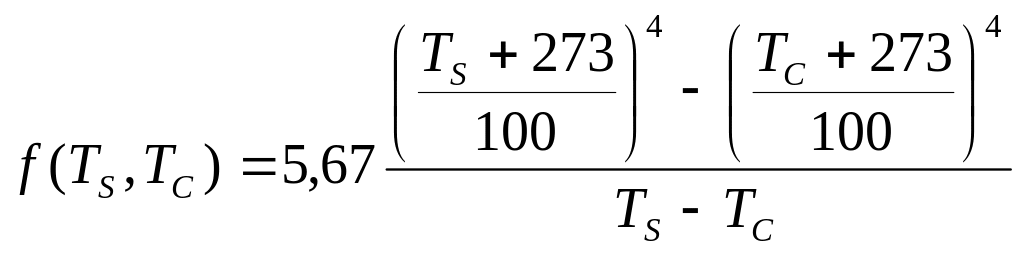(12)

,

тогда

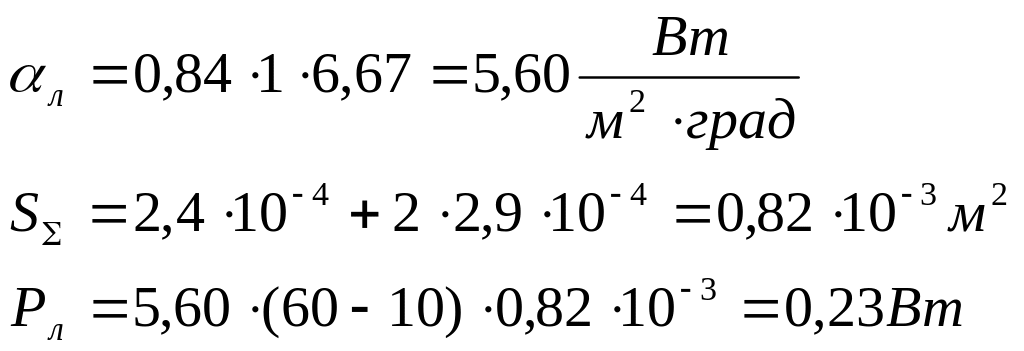
7. Найдем полную мощность Р_Σ, Вт, рассеиваемую поверхностью МЭУ при нормальном давлении p₀=760 мм.рт.ст. [1]:

(13)

8. Конвекция в неограниченном пространстве изменяется с давлением газа. Если конвективный коэффициент теплообмена при нормальном давлении p₀ равен α_к, а при давлении p – α_кp, то между этими параметрами при 1 мм.рт.ст.≤p≤10 атм. Существует следующая связь [1]:

, (14)

где n – показатель степени, соответствующий показателю степени при разности температур T-T_С в формулах (2)-(4) (для теплообмена между поверхностью тела и неограниченной средой при законе теплообмена ¼, для теплопередачи через неограниченные и ограниченные прослойки 2n=0,5).

Рассчитаем конвективные коэффициенты теплоотдачи и рассеиваемые мощности при p=300 мм.рт.ст. для всех поверхностей МЭУ:

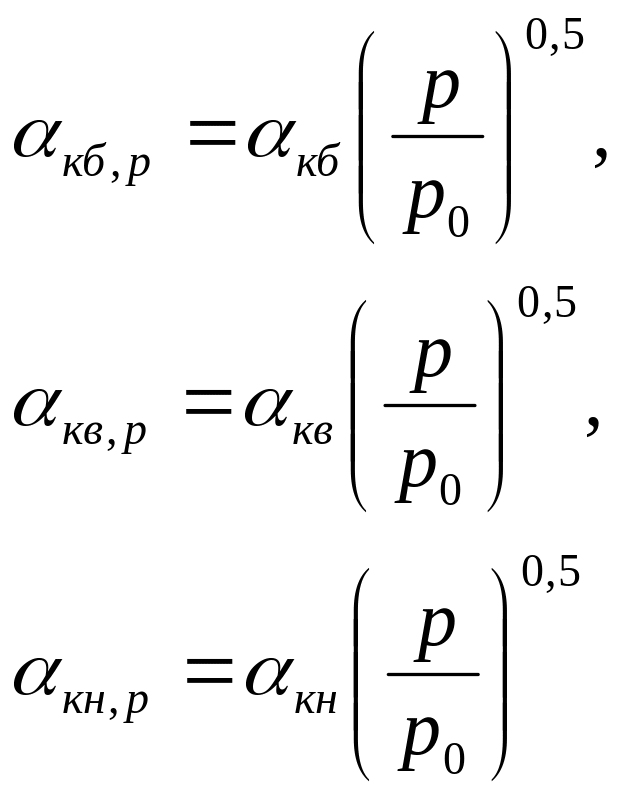(15)

(16)

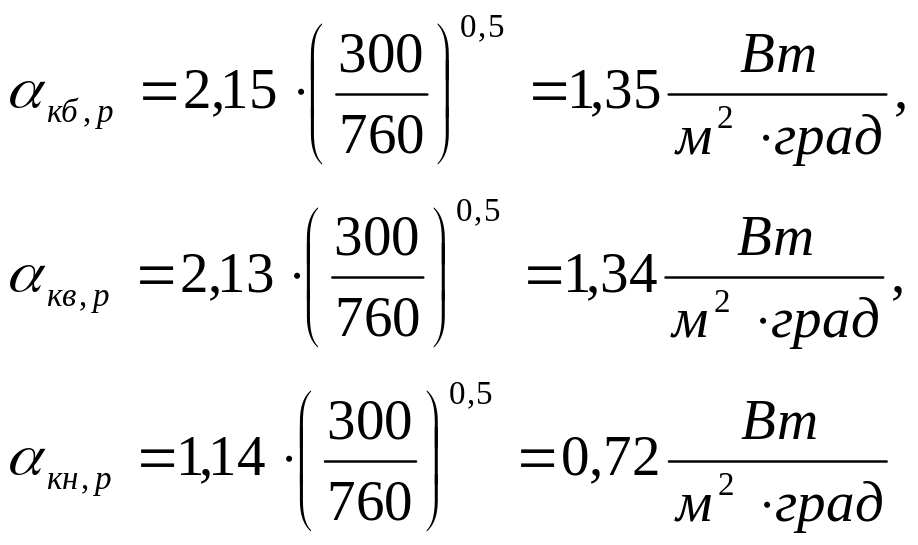
9. Найдем суммарную мощность, рассеиваемую всеми поверхностями МЭУ в результате конвекции, Р_Σк, Вт:

(17)

10. Мощность, рассеиваемая МЭУ в результате конвекции и излучения, определим по формуле (13):

11. Расчеты для диапазона давлений p=300…900 мм.рт.ст. приведены в таблице 1

Таблица 1 – Результаты расчетов

Давление p, мм.рт.ст.	Конвективный коэффициент αк,р, Вт/м2·град			Рассеиваемая в результате конвекции мощность Рб,р, Вт			Суммарная конвективная мощность всех поверхностей РΣк, Вт	Мощность, рассеиваемая в результате конвекции и излучения РΣ, Вт
	бок.	верх.	нижн.	бок.	верх.	нижн.
300	1,35	1,34	0,72	0,016	0,019	0,010	0,045	0,275
400	1,56	1,54	0,83	0,019	0,022	0,012	0,053	0,283
500	1,74	1,73	0,92	0,021	0,025	0,013	0,059	0,289
600	1,91	1,89	1,01	0,023	0,027	0,015	0,065	0,295
700	2,06	2,04	1,09	0,025	0,030	0,016	0,071	0,301
800	2,21	2,19	1,17	0,027	0,032	0,017	0,076	0,307
900	2,34	2,32	1,24	0,028	0,034	0,018	0,080	0,311

График зависимости Р = f( p ) приведен на рисунке 2.

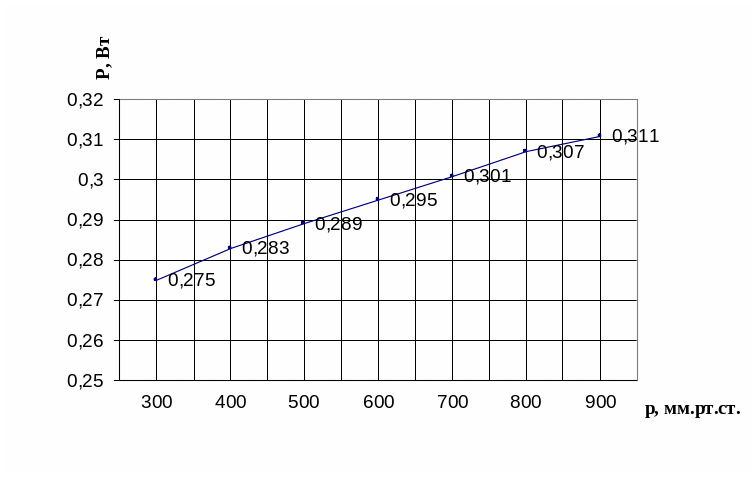
Рисунок 2 - График зависимости Р = f( p )

(построено при помощи программы Microsoft® Excel 2002)

9