Математическая запись второго начала термодинамики для обратимых процессов

Для обратимо протекающих процессов математическая запись второго начала термодинамики записывается в виде:

, (1.53)

где – приведенная теплота.

Для обратимых процессов в изолированной системе энтропия является постоянной величиной:

. (1.54)

Таким образом, для обратимых процессов второе начало термодинамики выступает как закон о существовании и сохранении энтропии.

Энтропия – функция состояния системы, ее изменение не зависит от пути процесса, а зависит только от начального и конечного состояния системы.

Энтропия – величина аддитивная. Энтропия равновесной системы равна сумме энтропий отдельных ее частей, а изменение энтропии всей системы равно сумме изменений энтропий ее частей. Изменение энтропии в сложном процессе равно сумме изменений энтропий в отдельных стадиях процесса:

ΔS_{процесса} = ΔS₁ + ΔS₂ + ΔS₃. (1.55)

Математическая запись второго начала термодинамики для необратимых процессов

Для необратимо протекающих процессов следствием второго начала термодинамики являются неравенства:

. (1.56)

Так как теплота в необратимом процессе меньше, чем в обратимом, то математическая запись второго начала термодинамики имеет вид:

. (1.57)

Для необратимых самопроизвольных процессов в изолированной системе:

. (1.58)

Таким образом, для необратимых процессов второе начало термодинамики выступает как закон о существовании и возрастании энтропии.

Для обратимых и необратимых процессов математическая запись второго начала термодинамики имеет вид:

или . (1.59)

Знак равенства соответствует обратимым процессам, знак неравенства – необратимым.

Для изолированных систем:

. (1.60)

Таким образом, в изолированных системах самопроизвольно могут совершаться лишь такие процессы, в результате которых энтропия системы возрастает; процесс идет до тех пор, пока энтропия не достигнет максимального для данных условий значения.

Подставляя вместо δQ выражение из первого начала термодинамики, получим объединенное уравнение первого и второго начал термодинамики:

. (1.61)

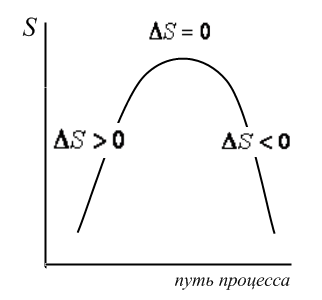
Изменение энтропии как критерий направления процесса в изолированной системе

Изменение энтропии является критерием направления процесса в изолированной системе. Изолированная система имеет постоянную внутреннюю энергию и постоянный объем (U, V=const).

Рис.1.3. Изменение энтропии при протекании процесса

Если , то в изолированной системе протекает обратимый равновесный процесс. В этом случае энтропия достигает максимально возможной величины. Если , то в изолированной системе протекает необратимый самопроизвольный процесс. Если , то в изолированной системе протекает необратимый не самопроизвольный процесс. Такие процессы термодинамически не вероятны и в изолированной системе не осуществимы.

Расчет изменения энтропии в различных процессах

Большинство реальных процессов необратимо, то есть рассчитать энтропию нельзя.

Так как энтропия является функцией состояния системы, то ее изменение в обратимом и необратимом процессе одинаково. Для вычисления изменения энтропии в данном реальном необратимом процессе, этот процесс (мысленно) разбивают на стадии, которые проводятся обратимо и вычисляют для них изменение энтропии для обратимых процессов, суммируют изменение энтропии всех обратимых стадий и получают изменение энтропии в данном необратимом процессе.

Например, для расчета изменения энтропии в необратимом процессе нагревания льда, находящегося при Т= –10°С до состояния жидкой воды при Т=10°С (ΔS_проц), процесс разбиваем на три обратимые стадии: стадию нагревание льда от Т= –10°С до Т=0°С (ΔS₁); стадию фазового перехода – плавления льда (ΔS₂); стадию нагревания воды от Т=0°С до Т=10°С (ΔS₃), тогда: ΔS_{процесса} = ΔS₁ + ΔS₂ + ΔS_3.

ΔS_проц

H ₂O_(тв)(Т=-10°С) H₂O_(ж)(Т=10°С)

ΔS₁ нагревание нагревание ΔS₃

ΔS₂

H₂O_(тв)(Т=0°С) H₂O_(ж)(Т=0°С)

фазовый переход

Рассмотрим, как рассчитывается энтропия в различных процессах.

1. Расчет изменения энтропии в процессе фазового перехода

Процессы фазового перехода (плавление, испарение, возгонка) проходят при постоянной температуре (Т=const). Изменение энтропии рассчитывают по уравнениям:

; (1.62)

, (1.63)

где ΔU_ф.п. и ΔН_ф.п. – теплоты фазового перехода, Т – абсолютная температура фазового перехода, n – число моль.

2. Расчет изменения энтропии при нагревании жидких или твердых тел от Т₁ до Т₂

а) процесс протекает при постоянном объеме и теплоемкости (V, C_V = const):

, (1.64)

б) процесс протекает при постоянном давлении и теплоемкости (р, C_р = const):

, (1.65)

в) процесс протекает при постоянном давлении (р = const), теплоемкость зависит от температуры (C_р = а+bT+cT²):

. (1.66)

3. Расчет изменения энтропии при нагревание идеального газа от Т₁ до Т₂

а) процесс протекает при постоянной теплоемкости газа (C_V = const):

, (1.67)

б) при протекании процесса теплоемкость зависит от температуры (C_V = а+bT+cT²):

. (1.68)

4. Расчет изменения энтропии при взаимной диффузии газов

Изменение энтропии при взаимной диффузии двух идеальных газов с образованием 1 моль смеси газов рассчитывается по уравнению:

, (1.69)

где х – мольная доля газа в смеси:

; . (1.70)

5. Расчет изменения энтропии в обратимо работающем электрохимическом элементе

Изменение энтропии при необратимой химической реакции, протекающей при постоянном давлении и температуре, например, в обратимо работающем электрохимическом элементе рассчитывается по уравнению:

, (1.71)

где ΔН – тепловой эффект химической реакции; – максимально полезная работа химической реакции, то есть работа химической реакции, которую можно определить, например, по ЭДС обратимо работающего электрохимического элемента ( ); z – число электронов, участвующих в электродной реакции на одну реагирующую частицу; F – постоянная Фарадея, равная 96500 Кл; Е – электродвижущая сила электрохимического элемента.