
- •2 X из неравенства
- •X X вытекает неравенство:
- •3 Основными элементарными функциями называются следующие функции.
- •4. Геометрический смысл производной
- •Правила дифференцирования
- •Дифференцирование сложной и обратной функций
- •Аблица производных простейших элементарных функций
- •Производные высших порядков
- •2.Необходимый признак экстремума.
- •3.Первый достаточный признак наличия или отсутствия экстремума.
- •Понятие первообразной функции. Теорема о первообразных.
- •Неопределенный интеграл, его свойства.
Аблица производных простейших элементарных функций
Легко получить следующую таблицу производных основных элементарных функций, используя определение производной. Для более подробного изучения данного материала рекомендуем использовать, например, "Математический анализ" ч.1 В.А. Ильина, В.А. Садовничего, Бл.Х. Сендова.
(u(x))' = u-1(x)u'(x), в частности,
(1/u(x))'
= -u'(x)/u2(x),
(![]() )'
= u'(x)/2
;
)'
= u'(x)/2
;
(logau(x))' = (u'(x)logae)/u(x) при 0<a1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x);
(au(x))' = au(x)ln a u'(x) при 0<a1, в частности, (eu(x))' = u'(x)eu(x);
(sin u(x))' = cos u(x)u'(x);
(cos u(x))' = -sin u(x)u'(x);
(tg u(x))' = u'(x)/cos2u(x) x/2+ n, n=0,+-1,...;
(ctg u(x))' = -u'(x)/sin2u(x) x n, n=0,+-1,...;
(arcsin u(x))' = u'(x)/
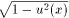 ,
-1<u(x)<1;
,
-1<u(x)<1;(arccos u(x))' = -u'(x)/ , -1<u(x)<1;
(arctg u(x))' = u'(x)/(1+u2(x));
(arcctg u(x))' = -u'(x)/(1+u2(x)).
Введем гиперболические функции:
sh x = (1/2)(ex-e-x)- гиперболический синус;
ch x = (1/2)(ex+ex)- гиперболический косинус;
th x = sh x/ch x -гиперболический тангенс;
cth x = ch x/sh x - гиперболический котангенс.
Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.
(sh x)' = ch x;
(ch x)' = sh x;
(th x)' = 1/ch2 x;
(cth x)' = -1/sh2 x.
Пример 7. Найти y', если
y(x) = x3arcsin x.
![]()
y(x) = ln sin (x2+1).
y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1)
Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.
9
вверху штрих:
![]()
Сначала находим
производную внешней функции ![]() (синуса),
смотрим на таблицу производных
элементарных функций и замечаем,
что
(синуса),
смотрим на таблицу производных
элементарных функций и замечаем,
что ![]() . Все
табличные формулы применимы и в том,
случае, если «икс» заменить сложным
выражением,
в данном случае:
. Все
табличные формулы применимы и в том,
случае, если «икс» заменить сложным
выражением,
в данном случае:
![]()
Обратите
внимание, что внутренняя функция ![]() не
изменилась, её мы не трогаем.
не
изменилась, её мы не трогаем.
Ну
и совершенно очевидно, что ![]()
Результат
применения формулы ![]() в
чистовом оформлении выглядит так:
в
чистовом оформлении выглядит так:
![]()
Далее мы берем производную внутренней функции, она очень простая:
![]()
Постоянный
множитель обычно выносят в начало
выражения:
![]()
10
Производные высших порядков
Если
функция ![]() дифференцируема
при всех
дифференцируема
при всех ![]() ,
то мы можем рассмотреть функцию
,
то мы можем рассмотреть функцию ![]() ,
сопоставляющую каждой точке
,
сопоставляющую каждой точке ![]() значение
производной
значение
производной ![]() .
Эта функция
.
Эта функция ![]() называется
производной функции
называется
производной функции ![]() ,
или первой
производной от
.
(Иногда саму исходную функцию
называют нулевой
производной и
обозначают тогда
,
или первой
производной от
.
(Иногда саму исходную функцию
называют нулевой
производной и
обозначают тогда ![]() .)
Функция
.)
Функция ![]() ,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала ![]() ,
которую мы обозначим
,
которую мы обозначим ![]() и
назовём второй
производной функции
.
Если предположить, что вторая
производная
и
назовём второй
производной функции
.
Если предположить, что вторая
производная ![]() существует
во всех точках
,
то она может также иметь производную
существует
во всех точках
,
то она может также иметь производную ![]() ,
называемую третьей
производной функции
,
и т. д. Вообще,
,
называемую третьей
производной функции
,
и т. д. Вообще, ![]() -й
производной функции
называется
производная от предыдущей,
-й
производной функции
называется
производная от предыдущей, ![]() -й
производной
-й
производной ![]() :
:
![]()
если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.
При ![]() первую,
вторую и третью производные принято
обозначать штрихами:
первую,
вторую и третью производные принято
обозначать штрихами: ![]() или
или ![]() ;
при прочих
--
числом в скобках в верхнем индексе:
;
при прочих
--
числом в скобках в верхнем индексе: ![]() или
или ![]() .
.
Физический
смысл производной второго порядка
проясняется из того, что если первая
производная
задаёт
мгновенную скорость изменения значений
в
момент времени
,
то вторая производная, то есть производная
от
,
задаёт мгновенную скорость изменения
значений мгновенной скорости, то
есть ускорение значений
.
Следовательно, третья производная --
это скорость изменения ускорения (или,
что то же самое, ускорение изменения
скорости, поскольку, как очевидно следует
из определения, ![]() ).
).
Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.
Пример 4.19
Найдём вторую производную функции ![]() .
Первая производная равна
.
Первая производная равна
![]()
далее находим
![]()
11
Точки локального максимума (минимума) — значение переменной, при которой функция достигает своей наибольшей (наименьшей) величины. Такие точки еще называются точками экстремума.
Глобальный максимум (минимум) функции — наибольшее (наименьшее) значение функции при указанных ограничениях. Другое название — глобальные экстремумы.
При этом глобальные экстремумы обычно ищутся не на всей области определения функции, а лишь на некотором отрезке [a; b]. Важно понимать, что глобальный экстремум и значение функции в точке экстремума далеко не всегда совпадают. Поясним это на конкретном примере:
Задача. Найти точку минимума и минимальное значение функции y = 2x3 − 3x2 − 12x + 1 на отрезке [−3; 3].
Решение. Сначала найдем точку минимума, для чего вычислим производную: y’ = (2x3 − 3x2 − 12x + 1)’ = 6x2 − 6x − 12.
Найдем критические точки, решив уравнение y’ = 0. Получим стандартное квадратное уравнение: y’ = 0 ⇒ 6x2 − 6x − 12 = 0 ⇒ ... ⇒ x1 = −1, x2 = 2.
Отметим эти точки на координатной прямой, добавим знаки производной и ограничения — концы отрезка:
![]()
Масштаб картинки не имеет значения. Самое главное — отметить точки в правильной последовательности. Из школьного курса математики известно, что в точке минимума производная меняет знак с минуса на плюс. Отсчет всегда идет слева направо — в направлении положительной полуоси. Поэтому точка минимума одна: x = 2.
Теперь найдем минимальное значение функции на отрезке [−3; 3]. Оно достигается либо в точке минимума (тогда она становится точкой глобального минимума), либо на конце отрезка. Заметим, что на интервале (2; 3) производная всюду положительна, а значит y(3) > y(2), поэтому правый конец отрезка можно не рассматривать. Остались лишь точки x = −3 (левый конец отрезка) и x = 2 (точка минимума). Имеем: y(−3) = 2(−3)3 − 3(−3)2 − 12(−3) + 1 = −44; y(2) = 2*23 − 3*22 − 12*2 + 1 = −19.
Итак, наименьшее значение функции достигается на конце отрезка и равно −44.
Ответ: xmin = 2; ymin = −44
Из приведенных рассуждений следует важный факт, о котором многие забывают. Функция принимает максимальное (минимальное) значение не обязательно в точке экстремума. Иногда такое значение достигается на конце отрезка, и производная там не обязана равняться нулю.
Схема решения задач B11
Если в задаче B11 требуется найти максимальное или минимальное значение функции f(x) на отрезке [a; b], выполняем следующие действия:
Найти производную функции: f’(x).
Решить уравнение f’(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.
Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка [a; b]. Оставшиеся числа обозначим x1, x2, ..., xn — их, как правило, будет немного.
Подставим концы отрезка [a; b] и точки x1, x2, ..., xn в исходную функцию. Получим набор чисел f(a), f(b), f(x1), f(x2), ..., f(xn), из которого выбираем наибольше или наименьшее значение — это и будет ответ.
12
связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.
С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
П р и м е р . |
Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существуеткасательной к графику этой функции. ( Подумайте, почему ? )
|
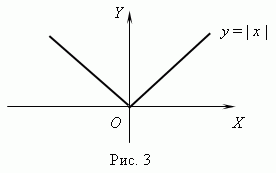
Достаточные признаки монотонности функции.
Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.
Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

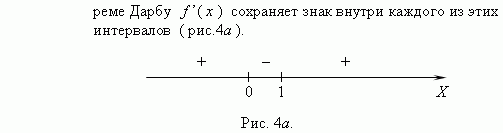
Следовательно,
функция возрастает на интервалах
( ![]() 0
) и ( 1,
+
и
убывает на интервале ( 0,
1 ).
Точка x =
0 не
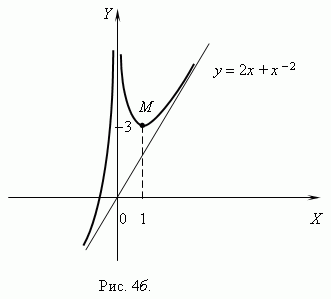
входит в область определенияфункции, но по мере приближения x к 0
слагаемое x 2 неограниченно возрастает,
поэтому функция также неограниченно
возрастает. В точке x =
1 значение функции равно 3. В соответствии
с этим анализом мы можем построить
график функции ( рис.4б ) .
0
) и ( 1,
+
и
убывает на интервале ( 0,
1 ).
Точка x =
0 не
входит в область определенияфункции, но по мере приближения x к 0
слагаемое x 2 неограниченно возрастает,
поэтому функция также неограниченно
возрастает. В точке x =
1 значение функции равно 3. В соответствии
с этим анализом мы можем построить
график функции ( рис.4б ) .
13 Также к свойствам функции относятся возрастание и убывание функции, экстремумы.
Функция f возрастает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 > х1 , выполнено неравенство f(x2) > f(x1).
Функция f убывает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 > х1 , выполнено неравенство f(x2) < f(x1).
Иными словами, функция f называется возрастающей на множестве Р, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве Р, если большему значению аргумента соответствует меньшее значение функции. При построении графиков конкретных функций полезно предварительно найти точки минимума (xmin) и максимума (xmax).
Точка х0 называется точкой максимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ? f(x0).
Точка х0 называется точкой минимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ? f(x0).
Точки минимума и максимума принято называть точками экстремума.
Пример 9.
Найти точки экстремума, экстремумы функции y = x2+2x, и указать промежутки возрастания и убывания функции.
у = x2+2x, D(y) = R
y' = (x2+2x)' = 2x+2
y' = 0, т.е. 2х+2 = 0
2х = -2
х = -1
Исследуем знак производной справа и слева от крайней точки.
x = -2, y'= -4+2<0
x = 0, y'= 0+2>0
Так как производная меняет свой знак с «-» на «+», то х = -1, это точка минимума функции.
Так как функция непрерывна в точке х = -1, то функция возрастает на [-1;+?] и убывает на [-?;-1].
Точки экстремума: xmin = -1
Экстремумы функции: ymin = y(-1) = 1 - 2 = -1.
