1 постоянной величиной наз-ся вел-на сохраняющая одно и то же значение. Применной наз-ся вел-на к-ая значенно переаенной х из множества х ставится одно вполне определенное значение другой вел-ны х и обоз-ся множества х, то вел-на у наз-ся фнкцией вел-ны х и обоз-ся у=f(х). При этом вел-на х наз-ся независимой переменной или аргументом вел-на у зависимой переменной или функцией.

Существует несколько способов задания функции.

Табличный. Используется тогда, когда область определения состоит из

конечного множества чисел. Тогда для задания функции проще всего указать

таблицу, содержащую значения аргумента и соответствующие значения

функции. Например, таблица логарифмов. Другим примером могут быть

таблицы, содержащие данные о числе жителей, населяющих земной шар в

отдельные годы, расписания движения поездов и т.п.

Аналитический. При аналитическом способе задания функция может

быть задана явно, когда дано выражение у через x, т.е. формула имеет вид

y  f (x); неявно, когда х и у связаны между собой уравнением вида F(x, y)  0 ;

параметрически, когда соответствующие друг другу значения х и у выражены

через третью переменную величину t, называемую параметром.

Логический. Если функция описывается правилом ее составления,

например, функция Дирихле: f(x)= 1, если x – рациональное; f(x)= 0, если x –

иррациональное.

Графический. Состоит в изображении графика функции – множества

точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а

ординаты – соответствующие им значения функции y  f (x). Преимуществом

графического задания является его наглядность, недостатком – его

неточность

2

Под основными свойствами функции y =f (x) будем понимать

следующие:

четность, нечетность. Функция y =f (x) называется четной, если для

любых значений х из области определения f (-x) =f (x) и нечетной, если

f (x)=-  f (x). В противном случае функция y =f (x) называется функцией

общего вида. График четной функции симметричен относительно оси ординат

(например, график функции

y =x2), а график нечетной функции симметричен

относительно начала координат (например, график функции

y =x3 ). Поэтому

для четной функции достаточно строить лишь правую половину графика

( x =>0 ), левая половина его ( x <=0 ) является зеркальным отражением правой

относительно оси Оу. Чтобы построить график нечетной функции, достаточно

изобразить правую половину его ( x=>0 ); левая половина графика ( x <= 0 )

получается в результате поворота правой на 180°.

монотонность. Если для любых значений x

1

, x

2  X из неравенства

1 2

X  X вытекает неравенство:

( ) ( )

1 2

f x  f x , то функция называется возрастающей;

( ) ( )

1 2

f x  f x , то функция называется неубывающей;

( ) ( )

1 2

f x  f x , то функция называется убывающей;

( ) ( )

1 2

f x  f x , то функция называется невозрастающей.

Возрастающие, невозрастающие, убывающие и неубывающие функции

на множестве X называются монотонными на этом множестве, а возрастающие

и убывающие – строго монотонными Интервалы, в которых функция

монотонна, называются интервалами монотонности.

ограниченность. Функция называется ограниченной на промежутке X,

если существует такое положительное число M  0 , что f (x)  M для любого

x X .

периодичность. Функция y  f (x) называется периодической, если

существует положительное число Т такое, что f (x  T)  f (x). Наименьшее

число с таким свойством называется периодом функции. Для построения

графика периодической функции достаточно изобразить его на отрезке, длина

которого равна периоду, а затем построить периодическое продолжение

графика. http://vfkomd.ru/docs/lections/matem%20190109/L2-Func.pdf

3 Основными элементарными функциями называются следующие функции.

Постоянная функция y  C , где C  R – постоянное число. График этой

функции есть прямая, параллельная оси Ох, находящаяся на расстоянии |С| от

оси Ох и расположенная выше оси Ох, если C  0, и ниже оси Ох, если C  0.

Степенная функция

a

y  x , где a  R – постоянное число. При a  0 эта

функция определена на всей действительной прямой. При a  0 она определена Лекция №2 «Функции и способы их задания»

5

на всей действительной прямой, за исключением точки х = 0. Примеры

графиков степенных функций, соответствующих различным показателям

степени, приведены на рис. 12

4. Геометрический смысл производной

.

Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е.

где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.

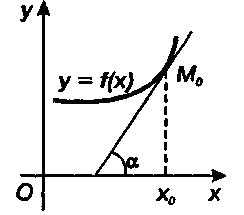
Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид

Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линииу = f(x) в точке Мо(хо, уо) запишется так:

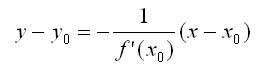
Физический смысл производной

Если x = f(t) - закон прямолинейного движения точки, то x’ = f’(t) — скорость этого движения в момент времени t. Быстрота протекания физических, химических и других процессов выражается с помощью производной.

Если отношение dy/dх при х->х0 имеет предел справа (или слева), то он называется производной справа (соответственно производной слева). Такие пределы называются односторонними производными.

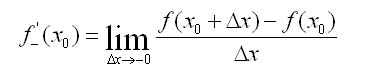
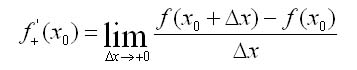
Очевидно, функция f{x) определенная в некоторой окрестности точки х0, имеет производную f’{x) тогда и только тогда, когда односторонние производные существуют и равны между собой.

Геометрическое истолкование производной как углового коэффициента касательной к графику распространяется и на этот случай: касательная в данном случае параллельна оси Оу.

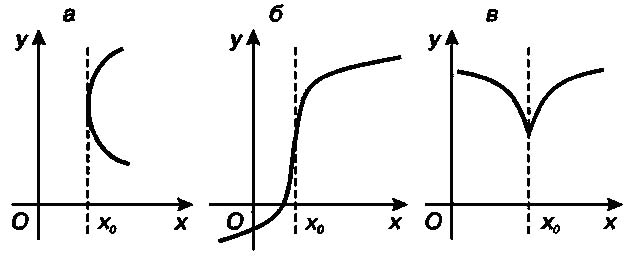
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.

5?

6 пределение 4 (дифференцируемость в точке). Функция f(x) называется дифференцируемой в точке x, если приращение  y этой функции в точке x представимо в виде

 y =A x + ( x)  x,

(1)

где A - некоторое число, не зависящее от  x, а lim_ x 0  ( x ) = 0.

В дальнейшем будем считать, что (0) = 0. В этом случае функция (x) будет непрерывной в точке  x = 0. Равенство 1 можно переписать иначе, так как функции  ( x),  x - бесконечно малые в точке  x = 0 и их произведение тоже бесконечно малая функция, поэтому

 y =A x +o( x).

(2)

Справедлива теорема

Теорема 1. Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на  x 0 получим

 y/ x = A+( x).

Переходя к пределу в последнем выражении при  x 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

lim_ x 0 y/ x = f'(x).

Обозначим ( x) =  y/  x-f'(x). Отсюда вытекает представление (1).

Пример 4. Доказать, что функция |x| не дифференцируема в точке x = 0.

Решение. Найдем приращение функции в точке x = 0 :

 y = | x|

Поэтому

lim_{ x -0} y/ x = -1, lim_{ x +0} y/ x = 1,

следовательно, функция |x| в точке x = 0 не дифференцируема.

Следующая теорема выражает связь между непрерывностью и дифференцируемостью.

Теорема 2 (дифференцируемость и непрерывность). Если  функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_ x 0 y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называетсякусочно гладкой.

7