Операционное исчисление
В основе операционного исчисления лежит преобразование Лапласа*. Множество функций-оригиналов отображается в множестве функций-изображений, при этом операции над оригиналами переходят в некоторые операции над изображениями. В частности, операции дифференцирования и интегрирования оригиналов переходят в действия соответственно умножения и деления во множестве изображений. Поэтому линейное дифференциальное уравнение в множестве оригиналов преобразуется в алгебраическое уравнение в множестве изображений. Решив полученное алгебраическое уравнение, находим прообраз его решения в множестве оригиналов, затем восстанавливаем решение исходного дифференциального уравнения.
Такова основная идея применений операционного вычисления как символического метода решения некоторых дифференциальных уравнений и систем дифференциальных уравнений.
В настоящее время операционное исчисление широко используется для решения многих прикладных задач, в частности задач радиотехники и электротехники.
22.1. Оригинал. Изображение
Оригиналом
или начальной
функцией называется
функция
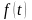действительного переменного
,
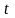удовлетворяющая следующим условиям:
1)
;
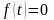2)
при
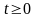функция
имеет на каждом отрезке конечной длины
пустое или конечное множество точек
разрыва первого рода;
3)
при
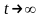функция
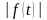возрастает не быстрее показательной
функции, т.е.
,
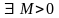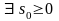такие, что выполняется
неравенство
,
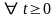
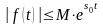обычно под числом
–
показателем роста функции
– понимается наименьшее из
возможных
чисел.
ПРИМЕР
1. Единичная функция
Хевисайда*
обозначается через
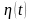и записывается в виде
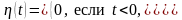график ее представлен на рисунке.
Функция
является оригиналом, причем
,
.
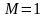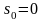Очевидно,
что для произвольной функции
,
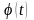определенной на
и удовлетворяющей условиям 2 и 3,
произведение
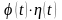является оригиналом (например,
,
и т.д.)
ПРИМЕР
2. Функция
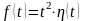является оригиналом, причем для всех
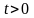имеем
,
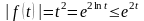т.е.
,
.
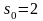ПРИМЕР
3. Функция
не является оригиналом, поскольку в
точке
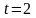функция имеет разрыв второго рода.
ПРИМЕР
4. Функция
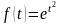не является оригиналом, так как при
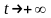растет быстрее любой показательной
функции вида
.
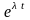Нетрудно проверить, что произведение оригинала на число, сумма и произведение конечного множества оригиналов есть также оригинал.
Изображением
(по Лапласу) оригинала
называется
комплекснозначная функция
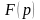комплексной переменной
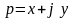(иногда
),
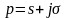определяемая интегралом Лапласа:
.
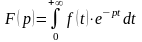(1)
Здесь
интегрирование проводится по действительной
переменной
,
,
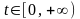т.е. интеграл (1) является несобственным,
зависящим от параметра
,
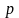причем область определения функции
является совокупностью тех комплексных
чисел
,
для которых интеграл (1) имеет смысл.
Переход от оригинала к изображению по формуле (1) есть преобразование Лапласа (сокр. ПЛ); будем обозначать его так:
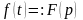
(читается: "оригиналу соответствует изображение ").
Теорема (существования изображения)
Пусть
– показатель роста функции
.
Тогда интеграл Лапласа сходится для
всех
таких, что
,
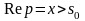причем для
,
удовлетворяющих условию
(
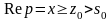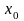– некоторое число, большее
),
сходимость является равномерной.
Справедливость
теоремы следует из соотношений:
,
и оценки модуля интеграла Лапласа
,
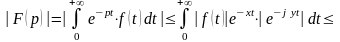
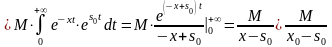(2)
верной
для всех
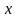из промежутка
.
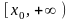Следствие. Из соотношения (2) имеем равенство
.
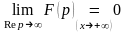(3)
Теорема (об аналитичности изображения)
Изображение Лапласа для оригинала с показателем роста является аналитической функцией переменной в области .
Доказательство теоремы проводится аналогично.
Теоремы показывают, что не всякая функция от может быть изображением некоторого оригинала. Изображение должно быть аналитической функцией комплексной переменной, в частности, удовлетворяющей условию (3), в области . Впредь будем рассматривать в области ее существования.
ПРИМЕР
5. Изображение для
оригинала
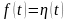найдем по формуле (2), а именно:
,
.
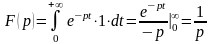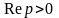Здесь
при подстановке верхнего предела имеем
,
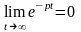так как
,
.
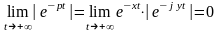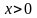Итак,
,
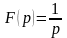т.е. получаем соотношение
.
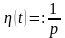ПРИМЕР
6. Часто используется
оригинал
,
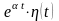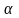– действительное или комплексное число,
а именно:
,
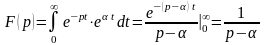т.е.
.
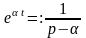Здесь
предполагается, что
,
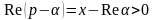т.е.
.
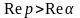В частности, изображение функции
,
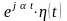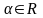находится аналогично и определяется
соотношением
,
.
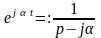Заметим, что иногда для краткости записи оригинала множитель опускается, и оригинал вида записывается в виде .