
- •2 Расчет балки от подвижной нагрузки
- •2.1 Определение реакций опор
- •2.2 Определение перерезывающих сил и изгибающих моментов
- •3 Проверка балки на жестксть, общую и местную устойчивость
- •3.2 Расчет ригеля на общую устойчивость
- •3.3 Расчет ригеля на местную устойчивость
- •3.4 Расчет ригеля на выносливость
- •1.Выбор конструкционных материалов
- •4 Расчет стоек рамы на прочность и подбор сечения
- •5 Проверка стержней на гибкость , жесткость и устойчивость
- •6 Подбор и расчет опорных баз
- •Степень унификации и стандартизации
- •Список использованных гост
- •Заключение
2 Расчет балки от подвижной нагрузки
2.1 Определение реакций опор
При решении подавляющего числа инженерных задач, рассматривающих действие подвижной нагрузки, прибегают к расчету по так называемому методу линий влияния. Этот метод основан на использовании принципа независимости действия сил, согласно которому каждая из сил, действующих на упругое тело, создает определенный, соответствующий данной силе эффект вне зависимости от действия других сил на то же тело. Таким образом, суммарный эффект от действия системы сил равен сумме результатов от действия каждой из сил.
Пусть на балке ab (рисунок 2.1 а) перемещается груз Р. Предположим, что груз в данный момент находится на расстоянии х от опоры а. Из уравнения моментов всех сил относительно опоры b находим:
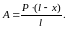
(2.1)

Рисунок 2.1 – Линия влияния опорных реакций
Поскольку переменная х входит в уравнение в первой степени, линия влияния опорной реакции А (рисунок 2.1б) будет изменяться по линейному закону (l-х)/l и для ее нахождения требуются две ординаты: А = Р = 30 кН при х = 0 и А = 0 при x = l. Аналогично может быть построена линия влияния и для опорной реакции В, причем:

(2.2)
При x = 0 В = 0, а при х = l В = P = 30 кН. Опорные реакции, направленные вверх, считаем положительными, а вниз - отрицательными.
2.2 Определение перерезывающих сил и изгибающих моментов
Рассмотрим
сечение k
балки ab (рисунок 2.2а), находящееся на
расстоянии
 от левой опоры и
от левой опоры и
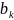 от правой опоры. Очевидно, что максимальный
изгибающий момент будет в центре балки,
т. е.
=
= l/2
= 3,2/2 = 1,6 м. Линия изгибающего момента
представлена на рисунке 2.2б.
Пока груз Р находится правее сечения
k,
левее сечения из внешних сил имеется
только опорная реакция А, и момент в
сечении k
равен:
от правой опоры. Очевидно, что максимальный
изгибающий момент будет в центре балки,
т. е.
=
= l/2
= 3,2/2 = 1,6 м. Линия изгибающего момента
представлена на рисунке 2.2б.
Пока груз Р находится правее сечения
k,
левее сечения из внешних сил имеется
только опорная реакция А, и момент в
сечении k
равен:
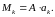
(2.3)
При
x
= 0 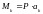 = 30
= 30
 1,6
= 48 кН
м;
1,6
= 48 кН
м;
При
x
= l  =0.
=0.
По этому уравнению строится правая ветвь линии влияния, где находится груз Р. При нахождении груза левее сечения k удобнее рассматривать правую часть балки, так как из внешних сил в правой части остается одна опорная реакция В и можно записать:
 (2.4)
(2.4)
При x = 0 =0.
При
x
= l 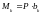 = 30
1,6
= 48 кН
м;
= 30
1,6
= 48 кН
м;
По этим данным строится левая ветвь линии влияния.

Рисунок
2.2 Влияния изгибающего момента
и
перерезывающей силы

Как
видно, обе ветви линии влияния пересекаются
под сечением k.
Ордината линии влияния в этом случае
имеет максимальное значение и равна
 .
При определении знака линии влияния
будем считать момент положительным,
если он вызывает растяжение в нижнем
волокне. Положительные значения ординат
линии влияния изгибающих моментов будем
откладывать со стороны растянутого
волокна.
.
При определении знака линии влияния
будем считать момент положительным,
если он вызывает растяжение в нижнем
волокне. Положительные значения ординат
линии влияния изгибающих моментов будем
откладывать со стороны растянутого
волокна.
Максимальный изгибающий момент равен:

( 2.5)
2.5)
Линия
влияния перерезывающей силы
 представлена на рисунке 2.2в. При этом
,
будет положительной, если внутренние
силы в сечении к стремятся вращать
отдельные части балки относительно ее
опор по часовой стрелке. В противном
случае
-
будет отрицательной (рисунок 2.2г).
представлена на рисунке 2.2в. При этом
,
будет положительной, если внутренние
силы в сечении к стремятся вращать
отдельные части балки относительно ее
опор по часовой стрелке. В противном
случае
-
будет отрицательной (рисунок 2.2г).
Следует отметить, что при определении реакций опор и перерезывающих сил ординаты линий влияния являются безразмерными величинами, а при определении изгибающих моментов - имеют единицы измерения длины.
Для стали ВСтЗсп подбираем балку в виде двутавра. Для определения номера профиля двутавра используем формулу:
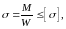
(2.6)
где
W- момент сопротивления,
 ;
;
М — максимальный изгибающий момент, Н м;
[σ] - допускаемое напряжение, для стали ВСтЗсп [σ] = 380 МПа.
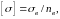
(2.7)
г де
де
 -
коэффициент запаса прочности,
=2,4.
-
коэффициент запаса прочности,
=2,4.
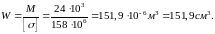
По W выбираем по ГОСТ 8239-76 двутавр №24 [5], для которого
 =
3460
=
3460
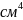 ,
,
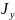 = 198
,
= 198
,
 = 289
= 289
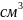 ,
,
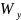 = 34,5
,
= 34,5
,
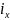 = 9,97
см,
= 9,97
см,
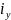 = 2,37
см,
= 2,37
см,
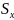 = 163
= 163
 ,
h
= 240
мм, b
= 115 мм,
d
= 5,6
мм, t
= 9,5
мм, R
= 10,5
мм, r
= 4 мм,
А = 34,8
,
,
h
= 240
мм, b
= 115 мм,
d
= 5,6
мм, t
= 9,5
мм, R
= 10,5
мм, r
= 4 мм,
А = 34,8
,
 = 27,3 кг.
= 27,3 кг.
