48. Критерий Дарбина – Уотсона для обнаружения автокорреляции. Нижние и верхние границы критических точек Дарбина – Уотсона.

Данный критерий используется для проверки наличия автокорреляции остатков. Он является наиболее часто используемым тестом. Проверка гипотезы о наличии автокорреляции осуществляется за несколько шагов, при этом имеют место зоны неопределенности, где оценить указанное явление не удается.

1-й шаг. Рассчитываем статистику Дарбина-Уотсона по формуле:

.

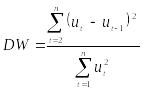Значение данной статистики может быть в интервале от 0 до 4.

2-й шаг. Для заданного уровня значимости , числа степеней свободы, равного числу факторов, включенных в модель, и числа наблюдений находим значения и  верхнюю и нижнюю границы. Если рассчитанное значение критерия расположено в районе двух, то автокорреляция остатков отсутствует. Положительная автокорреляция имеет место, когда , отрицательная – когда . При этом необходимо учитывать найденные верхнюю и нижнюю границы критерия. Окончательный вывод о наличии или отсутствии автокорреляции можно сделать на основе сопоставления рассчитанного значения с приведенной ниже шкалой.

При значение критерия , при и при .

49. Коэффициент автокорреляции первого порядка и его применение для раскрытия неопределенности в критерии Дарбина-Уотсона.

Данный критерий используется для проверки наличия автокорреляции остатков. Он является наиболее часто используемым тестом. Проверка гипотезы о наличии автокорреляции осуществляется за несколько шагов, при этом имеют место зоны неопределенности, где оценить указанное явление не удается.

1-й шаг. Рассчитываем статистику Дарбина-Уотсона по формуле:

.

Значение данной статистики может быть в интервале от 0 до 4.

2-й шаг. Для заданного уровня значимости , числа степеней свободы, равного числу факторов, включенных в модель, и числа наблюдений находим значения и  верхнюю и нижнюю границы. Если рассчитанное значение критерия расположено в районе двух, то автокорреляция остатков отсутствует. Положительная автокорреляция имеет место, когда 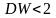, отрицательная – когда . При этом необходимо учитывать найденные верхнюю и нижнюю границы критерия. Окончательный вывод о наличии или отсутствии автокорреляции можно сделать на основе сопоставления рассчитанного значения с приведенной ниже шкалой.

При значение критерия , при и при .

50. Регрессионные уравнения с переменной структурой. Фиктивные переменные, виды фиктивных переменных. Преимущества использования фиктивных переменных при построении регрессионных моделей.

На практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести: пол (мужской, женский), образование (начальное, среднее,

высшее), фактор сезонности (зима, весна, лето, осень) и т. п.

Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В

этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.

Фиктивная переменная — это индикаторная пе­ременная, отражающая качественную характеристику. Это могут быть разного рода атрибутивные призна­ки, такие, например, как профессия, пол, образование, климати­ческие условия, принадлежность к определенному региону.

В регрессионных моделях с временными рядами используется три основных вида фиктивных переменных:

1) Переменные-индикаторы принадлежности наблюдения к определенному периоду — для моделирования скачкообразных структурных сдвигов. Границы периода (моменты “скачков”) должны быть установлены из априорных соображений. Например, 1, если наблюдение принадлежит периоду 1941-45 гг. и 0 в противном случае. Это пример использования для моделирования временного структурного сдвига. Постоянный структурный сдвиг моделируется переменной равной 0 до определенного момента времени и 1 для всех наблюдений после этого момента времени.

2) Сезонные переменные — для моделирования сезонности. Сезонные переменные принимают разные значения в зависимости от того, какому месяцу или кварталу года или какому дню недели соответствует наблюдение.

3) Линейный временной тренд — для моделирования постепенных плавных структурных сдвигов. Эта фиктивная переменная показывает, какой промежуток времени прошел от некоторого “нулевого” момента времени до того момента, к которому относится данное наблюдение (координаты данного наблюдения на временной шкале). Если промежутки времени между последовательными наблюдениями одинаковы, то временной тренд можно составить из номеров наблюдений.

Использование фиктивных переменных имеет следующие преимущества:

1. Интервалы между наблюдениями не обязательно должны быть одинаковыми. В выборке могут быть пропущенные наблюдения.

2. Коэффициенты при фиктивных переменных легко интерпретировать, они наглядно представляют структуру динамического процесса.

3. Для оценивания модели не приходится выходить за рамки классического метода наименьших квадратов.