43. Критерий µ обнаружения гетероскедастичности.

-критерий

Используется для проверки гетероскедастичности при большом числе наблюдений исходных данных. Алгоритм метода распадается на пять шагов.

1-й шаг. Все наблюдения зависимой переменной разбиваются на групп в соответствии с уровнем изменения величины .

2-й шаг. Для каждой группы рассчитываются суммы квадратов отклонений

3-й шаг. Находится общая сумма квадратов отклонений по всем группам

4-й шаг. Вычисляется параметр по формуле

,

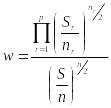где  общее число наблюдений;

 число наблюдений -й группы.

5-й шаг. Рассчитывается значение критерия по формуле

,

который приближенно соответствует критерию при числе степеней свободы , когда дисперсия всех наблюдений однородна.

Если при заданном уровне значимости , то имеет место гетероскедастичность.

44. Тест Гольдфельда-Квандта для обнаружения гетероскедастичности.

Как и в предыдущих случаях, тест Гольдфельда-Квондта проверяет гипотезу  гомоскедастичны против гипотезы  гетероскедастичны (с возрастающей дисперсией). Тест используется для значительных по объему выборок. При этом ставится условие, чтобы число наблюдений было, по крайней мере, в два раза больше числа переменных. Для проведения теста необходимо выполнить пять шагов.

1-й шаг. Ранжируем наблюдения в порядке возрастания значений независимой переменной . Если переменная не одна, то либо выбирают наиболее существенную с точки зрения постановки задачи, либо попеременно используют тест для каждой из переменных.

2-й шаг. Выбираем центральных наблюдений переменной и исключаем их из выборки. Число обычно принимают равным от одной четвертой до одной трети общего числа наблюдений. Остаток наблюдений делится на две подвыборки, первая из которых состоит из наименьших значений переменной, вторая – из наибольших.

3-й шаг. Строим две эконометрические модели на основе каждой из подвыборок, содержащих по наблюдений.

4-й шаг. Рассчитываем суммы квадратов остатков

и

для каждой из моделей, где  остатки, соответствующие первой модели,  остатки, соответствующие второй модели.

5-й шаг. Рассчитываем значение критерия

,

который в случае выполнения гипотезы о гомоскедастичности соответствует -распределению с числом степеней свободы и уровнем значимости . Рассчитанное значение критерия сравнивается с теоретическим (табличным) и в случае, когда , то гипотеза о гомоскедастичности величин принимается, т.е. гетероскедастичность отсутствует.

Можно заметить, что если имеет место гомоскедастичность, то дисперсии и для первой, и для второй модели совпадут, и значение критерия будет равно единице.

45. Обобщенный 2мнк и его отличие от классического 1мнк.

Метод 2МНК может быть обобщен и на случай большего числа уравнений и переменных.

Метод 2МНК имеет ряд особенностей, которые сводятся к следующему:

1. Оценки 2МНК все еще смещенные, но уже состоятельные. Чем больше выборка, тем более точные оценки системы одновременных уравнений мы получаем, тем меньше вариация получаемых оценок.

2. Смещение оценок, получаемых с помощью 2МНК для малых выборок, имеет противоположный знак по отношению к смещению оценок, получаемых с помощью 1МНК.

3. Если получаемые инструментальные переменные слабо подходят в качестве замены эндогенным переменным ( имеет низкое значение), то метод 2МНК не подходит для решения проблемы одновременных уравнений.

4. Если объясняющие (независимые) переменные сильно коррелируют друг с другом, то 2МНК не дает хороших результатов. Мультиколлинеарность ведет к смещению оценок.

5. -статистики для оценки значимости параметров, получаемых с помощью 2МНК, являются более точными по сравнению с их аналогами, получаемыми методом 1МНК.