4.5.11.1. Простая линейная регрессия

Простая линейная регрессия позволяет прогнозировать результат через определенный промежуток времени. При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.

Например, рассмотрим взаимосвязь между успешностью обучения математике (у), и показателем невербального интеллекта (х). Для этого выберите в меню Analyze... (Анализ)Regression...(Регрессия) Linear... (Линейная). Появится диалоговое окно Linear Regression (рис. 4.52).  Перенесите переменную rm в поле для зависимых переменных и присвойте переменнойnvi статус независимой переменной. Ничего больше не меняя, начните расчёт нажатием ОК.

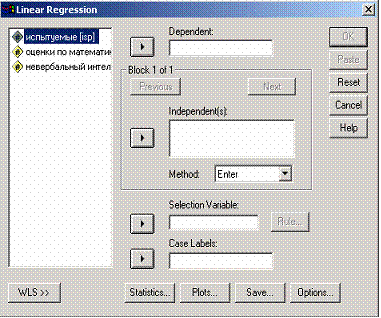
Рис.4.52: Диалоговое окно Линейная регрессия

Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах. Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить). Откроется диалоговое окно Linear Regression: Save как изображено на рисунке 4.53.

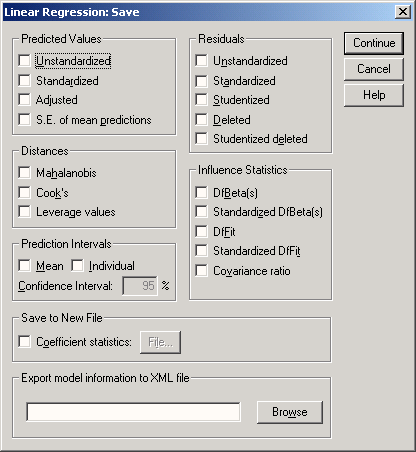
Рис. 4.53: Диалоговое окно Линейная регрессия: Сохранение

4.5.11.2. Множественная линейная регрессия

Множественная линейная регрессия используется в том случае, если в регрессионный анализ вовлекаются несколько переменных. Например, при анализе успешности обучения подростков психолог в дополнение к независимой переменной IQ рассматривает другие независимые переменные, влияющие, по его мнению, на успеваемость: мотивация, личностные качества и т. п. Для этого выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная). Поместите, например, переменную ozn в поле для зависимых переменных, а переменные: IQ,mot, otv, us объявите независимыми.

4.5.11.3. Нелинейная регрессия

Нелинейная регрессия используется для перевода нелинейных связей в линейную модель. Например, при сравнении баллов по третьему, математическому, субтесту теста Векслера (переменная Y) и оценками по алгебре (переменная X). Между переменными Y и X необходимо искать не линейные, а криволинейные связи. Для этого выберите в меню Analyze... (Анализ)Regression... (Регрессия) Nonlinear... (Нелинейная). В диалоговом окне Nonlinear Regression (Нелинейная регрессия) перенесите переменную bal в поле для зависимых переменных.  Щёлкните на поле Model Expression (Модельное выражение) и внесите в него необходимую формулу. При вводе формулы можно использовать клавиатуру, находящуюся в диалоговом окне (рис. 4.54). Затем задайте начальные значения параметров. Щёлкните на кнопке Parameter... (Параметр) и вы получите диалоговое окно, в котором сможете задавать начальные значения.

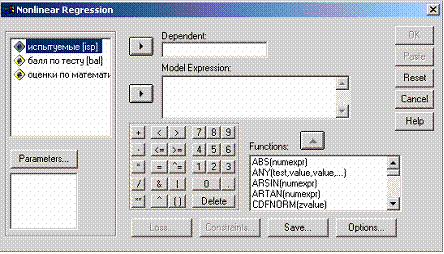
Рис. 4.54: Диалоговое окно Nonlinear Regression (Нелинейная регрессия).

Покиньте диалоговое окно нажатием кнопки. Далее.

 Щёлкните на кнопке Save (Сохранить). Отметьте в диалоговом окне Nonlinear Regression: Save New Variables (Нелинейная регрессия: Сохранить новые переменные) параметры:Predicted Values (Прогнозируемые значения) и Residuals (Остатки). Таким образом, Вы создадите две новые переменные, которые содержат вычисленные значения. Начните расчёт нажатиемОК.