Измерительные шкалы.

Любое научное исследование начмнается с того, что исследователь фиксирует выраженность интересующего его свойства у объекта исследования, как правило, при помощи чисел. В зависимости от того, какая операция лежит в основе измерения признака, выделяют измерительные шкалы. Шкалы разделяют на метрические (если есть или может быть установлена единица измерения) и неметрические (если единицы измерения не могут быть установлены). Определение того, в какой шкале измерено явление является ключевым моментом анализа данных: любой последующий шаг, выбор любого метода зависит именно от этого.

1.                    Номинативная шкала (номинальная шкала или шкала наименований) определяет, что разные свойства или признаки отличаются друг от друга, но не подразумевает каких-либо количественных операций с ними. Эта шкала неметрическая. Самая простая номинативная шкала называется дихотомической (измеряемые признаки можно кодировать любыми двумя отличающимися друг то друга символами). Например: пол (1-мужской, 2-женский), возраст (1-7 лет, 2-9 лет) и т.д.

2.                    Порядковая (ранговая, ординарная) шкала располагает измерительные признаки по рангу – от самого большого до самого маленького или наоборот. Эта шкала также относится к неметрической. При кодировании порядковых переменных им можно приписывать любые цифры (коды), но в этих кодах обязательно должен сохраняться порядок, т.е. каждая последующая цифра должна быть больше (или меньше) предыдущей. Например, испытуемым предложено определить выраженность изучаемого свойства, используя 5-бальную шкалу. Или пяти учащимся присвоены ранги в соответствии с тем, кто быстрее читает (ранг 1 – учащийся с самой высокой скоростью чтения). При сравнении испытуемых друг с другом мы можем сказать, больше или меньше выражено свойство, но не можем сказать, насколько или во сколько раз больше или меньше оно выражено.

3.                    Шкала интервалов (метрическая шкала) показывает, что каждое из возможных значений измеренных величин отстоит от ближайшего на равном расстоянии. При работе с этой шкалой измеряемому свойству или предмету присваивается число, равное количеству единиц измерения, пропорциональное выраженности измеряемого свойства. Особенность интервальной шкалы – произвольность выбора нулевой точки: ноль вовсе не соответствует полному отсутствию измеряемого свойства. Следовательно, применяя эту шкалу, мы можем судить, на сколько больше или меньше выражено свойство при сравнении объектов, но не можем судить во сколько раз больше или меньше выражено свойство.Например: сезонные изменения температуры воздуха; коэффициент интеллекта (IQ); возраст ит.д.

4.                    Шкала отношений (метрическая шкала). К этой шкале относятся все интервальные переменные, которые имеют абсолютную нулевую точку, соответствующую полному отсутствию выраженности измеряемого свойства. Например: измерения роста, веса, времени выполнения задачи, времени реакции и т.д.

Уровень статистической значимости.

Статистическая значимость это основной результат проверки статистической гипотезы.

При обосновании статистического вывода следует решить вопрос, где же проходит линия между принятием и отвержением нулевой гипотезы? Она базируется на понятии уровня значимости. Уровень значимости это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности употребляют латинскую букву p.

Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.

Существует общепринятая терминология, которая относится к доверительным интервалам вероятности. Высказывания, имеющие вероятность ошибки р <= 0,05. называются значимыми; высказывания с вероятностью ошибки р <= 0,01 - очень значимыми, а высказывания с вероятностью ошибки р <= 0,001 - максимально значимыми. Величины 0,05, 0,01 и 0,001 – это стандартные уровни статистической значимости. При статистическом анализе экспериментальных данных психолог в зависимости от задач и гипотез исследования должен выбрать необходимый уровень значимости. Рассмотрим пример интерпретации полученных значений при стандартном уровне статистической значимости 0,05.

 

Уровень значимости	Решение	Возможный статистический вывод
р > 0.1	Принимается Н0	Статистически достоверные различия не обнаружены.
р <= 0.1	Сомнения в истинности Н0, неопределенность	Различия обнаружены на уровне статистической тенденции.
р <= 0.05	Значимость, отклонение Н0	Обнаружены статистически достоверные (значимые) различия.
р <= 0.01	Высокая значимость, отклонение Н0	Различия обнаружены на высоком уровне статистической значимости.

В статистическом пакете SPSS используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначаемые буквой P, могут иметь различное числовое выражение в интервале от 0 до 1, например, P=0,8, P=0,25 или P=0,016. В-первых двух случаях полученные уровни значимости слишком велики, следовательно, результат не значим. В последнем же случае уровень достоверный.

 Критерии различий

 

Критерий Розенбаума	Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой выборке не менее 11 испытуемых. Применение критерия начинается с упорядочивания значений признака в обеих выборках по нарастанию или убыванию.	Гипотезы: Н0: Уровень признака в выборке 1 не превышает уровня признака в выборке 2. Н1: Уровень признака в выборке 1превышает уровня признака в выборке 2.	Ограничения: 1.                 В каждой выборке не менее 11 наблюдений. 2.                 Если выборок менее 50, разность между ними не больше 10. 3.                 Если 51-100, то не больше 20. 4.                 Если более 100, то разность более чем в 1,5-2 раза. 5.                 Диапазоны разброса значений в двух выборках должны не совпадать между собой.
Критерий Манна-Уитни (см. раздел 4.5.9.1)	Используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного (между малыми выборками).Эмпирическое значение критерия отражает то, на сколько велика зона совпадения между рядами. Чем меньше эмпирическое значение, тем более вероятно, что различия достоверны.	Гипотезы: Н0: Уровень признака в группе 2 не ниже уровня признака в группе 1. Н1: Уровень признака в группе 2 ниже уровня признака в группе 1.	Ограничения: 1.                 В каждой группе не менее 3 наблюдений (если впервой 2, то во второй- 5). 2.                 В каждой выборке не более 60 наблюдений.
Критерий Крускала-Уоллиса (см. раздел 4.5.9.3)	Используется для оценки различий между тремя и более выборками по уровню какого-либо признака. Рассматривается как непараметрический аналог метода дисперсионного однофакторного анализа для несвязанных выборок (сумма рангов).	Гипотезы: Н0: Между выборками 1, 2, 3 и т.д. существуют лишь случайные различия по уровню исследуемого признака. Н1: Между выборками 1, 2, 3 и т.д. существуют неслучайные различия по уровню исследуемого признака.	Ограничения: 1.                 При сопоставлении 3 выборок 3:2:2- различия на низшем уровне значимости; 3:3:3 (или 4:2:2)- на более высоком уровне значимости. 2.                 Критическое значение предусмотрено только для 3 выборок. Для 4 и более необходимо использовать таблицу критерия х2 3.                 При множественном сопоставлении выборок достоверные различия между какой-либо парой могут быть стерты.
Критерий тенденций Джонкира	Критерий предназначен для выявления тенденций изменения признака при переходе от выборки к выборке и при сопоставлении 3 и более выборок. Он позволяет упорядочить обследование выборки по какому-либо признаку (креативности, гибкости, толерантности и т.п.). Статистика критерия отражает степень преобладания. Чем выше эмпирическое значение, тем тенденция возрастания признака является более существенной.	Гипотезы: Н0: Тенденция возрастания значений признака при переходе от выборке к выборке является случайной. Н1: Тенденция возрастания значений признака при переходе от выборке к выборке не является случайной.	Ограничения: 1.                 В каждой выборке одинаковое число наблюдений. 2.                 Нижний порог не менее 3 выборок и не менее 2 наблюдений; верхний порог не более 6 выборок и не более 10 наблюдений.

 

Ранговая корреляция (взаимная связь).

Корреляционная связь – это согласованные изменения двух признаков. Отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого.

 

Коэффициент ранговой корреляции Спирмена (см. раздел 4.5.10.2)

Позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков. Ряды значений:         Два признака, измеренные в одной группе;         Две индивидуальные иерархии, выявленные у двух испытуемых по одному набору признаков;         Две групповые иерархии признаков;         Индивидуальная и групповая иерархии признаков.

Гипотезы: 1 вариант Н0: Корреляция между переменными А и Б не отличается от нуля. Н1: Корреляция между переменными А и Б достоверно отличается от нуля. 2 вариант Н0: Корреляция между иерархиями А и Б не отличается от нуля. Н1: Корреляция между иерархиями А и Б достоверно отличается от нуля.

Ограничения: 1.      По каждой переменной не менее 5 наблюдений. 2.      Коэффициент при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленное значение.

 

Корреляции

Корреляционный анализ – это проверка гипотез о связях между переменными с использованием коэффициентов корреляции. Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные.

Типы шкал:	Переменные X, Yколичественные	Переменные X, Y- качественные (номинативные)	Переменные X-качествен­ная, Y-коли­чественная
Задачи	Корреляционный анализ	Анализ номинативных дан­ных: классификаций, таб­лиц сопряженности, после­довательностей (серий)	Сравнения выбо­рок по уровню выраженности признака
Методы	а) г-Пирсона — для метрических Х и Y; б) частная корреляция и сравнение корреляций; в) r-Спирмена, t-Кендалла — для ранговых Х и Y	Критерий х2-Пирсона (для классификаций и таблиц сопряженности), критерий Мак-Нимара (для таблиц 2x2 с повторными измерениями), критерий серий (для последовательностей)	Параметрические и непараметрические методы сравнения

Для графического представления корреляционной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая; пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» для двух зависимых переменных можно построить путём вызова меню Graphs... (Графики) Scatter plots... (Диаграммы рассеяния). Например, построим диаграмму рассеяния между переменной компетентность и употребление алкоголя. Полученная диаграмма выглядит следующим образам:

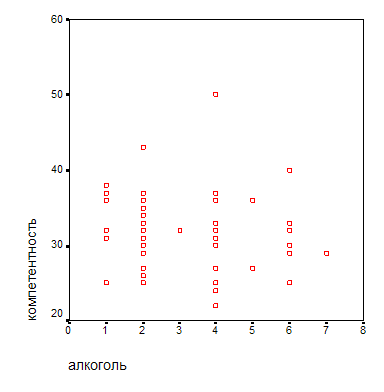
Проведение корреляционного анализа с помощью программы SPSS – проста и удобна. В программе предложены следующие методы вычисления коэффициента корреляции:

      коэффициент корреляции Пирсона (корреляция моментов произведений).

      ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.

       точечная двухрядная корреляция (одна из двух переменных является дихотомической). Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции.

       четырёхполевая корреляция (обе переменные являются дихотомическими). Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства.

Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следующие градации:

Значение	Интерпретация
До 0,2	Очень слабая корреляция
До 0,5	Слабая корреляция
До 0,7	Средняя корреляция
До 0,9	Высокая корреляция
Свыше 0,9	Очень высокая корреляция

Расчёт коэффициента корреляции между двумя недихотомическими переменными рассчитывается тогда, когда связь между ними линейная (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю.

В файле вывода результатов корреляционного анализа SPSS Output для каждого рассчитываемого критерия содержится квадратная таб­лица (Correlations). В каждой ячейке таблицы приведены: само зна­чение коэффициента корреляции (Correlation Coefficient), статисти­ческая значимость рассчитанного коэффициента (Sig.), количество испытуемых (N). В шапке и боковой графе полученной корреляци­онной таблицы содержатся названия переменных.

Напомним, что диагональ (левый верхний — правый нижний угол) таблицы состоит из единиц, т. к. корреляция любой переменной с самой собой является максимальной, то есть, равна единице. Табли­ца симметрична относительно этой диагонали (т. к. корреляция пе­ременной А с переменной Б тождественна корреляции Б с А), поэто­му нет смысла искать значимые «сильные» корреляции во всей таблице — достаточно лишь просмотреть треугольный фрагмент по­лученной матрицы над или под диагональю. Если вы оставили при­нятый в программе по умолчанию флажок «Отмечать значимые кор­реляции», то в итоговой корреляционной таблице будут отмечены статистически значимые коэффициенты: на уровне 0,05 и меньше — одной звездочкой (*), а на уровне 0,01 — двумя звездочками (**).

4.5.10.1. Коэффициент корреляции по Пирсону

Для вычисления коэффициента корреляции по Пирсону выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Bivariate... (Парные) Появится диалоговое окно Bivariate Correlations (рис. 4.48).

Рис. 4.48: Диалоговое окно Bivariate Correlations (Двумерные корреляции)

Исследуемые переменные по очереди внесите в поле тестируемых переменных. Расчет коэффициента по Пирсону является предварительной установкой, также как двухсторонняя проверка значимости и маркировка значимых корреляций. Начните расчет путем нажатия кнопки ОК.

При помощи щелчка на кнопке Options... (Опции) можно организовать расчёт среднего значения и стандартного отклонения для двух переменных. Дополнительно могут выводиться отклонения произведений моментов (значений числителя формулы для коэффициента корреляции) и элементы ковариационной матрицы (числитель, делённый на n - 1).

4.5.10.2. Ранговые коэффициенты корреляции по Спирману и Кендалу

При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Например, необходимо определить связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном». Для этого в диалоговом окне Bivariate Correlations... (Парные корреляции) уберите метку для расчета корреляции по Пирсону, установленную по умолчанию. Вместо этого активируйте расчет корреляции Спирмана.

Ещё одним вариантом ранговых коэффициентов корреляции являются коэффициенты Кендала (t-Кендала), расчет которых можно вызвать в диалоговом окне Bivariate Correlations... (Парные корреляции). Например, при изучении отношения к семейной жизни, психолог просит проранжировать семь личностных черт, имеющих определяющее значение для семейного благополучия. В этом методе одна переменная представляется в виде монотонной последовательности (например, данные мужа) в порядке возрастания величин; другой переменной (например, данные жены) присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов. Применение коэффициента Кендала является предпочтительным, если в исходных данных встречаются выбросы.

4.5.10.3. Частная корреляция

Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей переменной. Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи (корреляции) под влиянием общей причины. Например, общей причиной изменчивости двух переменных («третьей переменной») может являться возраст при изучении взаимосвязи различных психологических особенностей в группе детей разного возраста.

Для вычисления частной корреляции выберите в меню Analyse... (Анализ) Correlate... (Корреляция) Partial.... Откроется диалоговое окно Partial Correlations (Частные корреляции) (рис. 4.49).  Перенесите переменные, например, competent и alcogol в поле признаков, а переменную age в поле контрольных переменных и оставьте предварительную установку для двухстороннего теста значимости.

При помощи щелчка на кнопке Options... (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).

В случае одной искажающей переменной, возможен расчёт частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдаёт корреляции высших порядков. Начните расчёт щелчком на кнопке ОК.

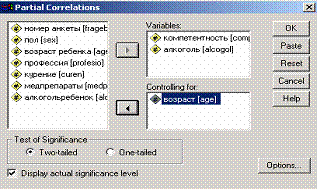
Рис. 4.49: Диалоговое окно Partial Correlations (Частичные корреляции)