1. Определение полуплоскости. Аксиома разбиения плоскости и свойства разбиения (сформулировать, сделать чертеж и символическую запись).

В геометрии третьим основным понятием, не определяемым через другие понятия, является понятие плоскости.

Плоскость не имеет границ. Представление о плоскости дает поверхность стола. Плоскость принято обозначать строчными греческими буквами: , , ….

Определение 1. Множество точек, состоящее из точек прямой а и точек, лежащих по одну сторону от прямой а, называется полуплоскостью, ограниченной прямой а. Прямая а называется границей полуплоскости, а точки, не лежащие на прямой а, называются внутренними точками полуплоскости.

Аксиома расположения точек относительно прямой на плоскости:

Прямая разбивает плоскость на две полуплоскости. При этом точки прямой и только они являются общими точками этих полуплоскостей.

Это разбиение обладает следующим свойством:

если концы какого-либо отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую а;

если концы какого-либо отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.

A  ; B  . AB  .

2. Определение медианы. Доказать свойство медианы равнобедренного треугольника, проведенной к его основанию. Сформулировать обратные теоремы.

О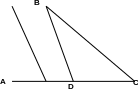 пределение 1. Медианой треугольника называ­ется отрезок, соединяющий вершину треугольника с середи­ной противоположной стороны.

BM –медиана, проведенная к сто­роне АC (АD = DC).

Теорема 1. В равнобедренном треугольнике медиана, проведенная к основанию, является его биссектрисой и высотой.

Д ано: ∆АВС; АВ = ВС; ВD – медиана.

Доказать: BD – биссектриса,

BD – высота.

Доказательство:

2. Из ∆ABD = ∆DBC 

ABD = DBC  BD – биссектриса.

3. Из ∆ABD = ∆DBC 

ADB = CDB.

4. ADB + CDB = 180. 2ADB = 180.

ADВ = ВDC = 90.

5. ADВ = ВDC = 90.  BD  AC  BD – высота.

Теорема 1а (обратная). В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.

Дано: ∆АВС; АВ = ВС, BD - биссектриса. Доказать: BD – медиана, BD – высота.

Доказательство:

2. Из ∆ABD = ∆DBC  AD = DC  AD – медиана по определению.

3. Из ∆ABD = ∆DBC  ADВ = ВDC.

Теорема 1б (обратная). В равнобедренном треугольнике высота, проведенная к основанию, является его медианой и биссектрисой.

Дано: ∆АВС; АВ = ВС, BD - высота. Доказать: BD – медиана, BD – биссектриса.

Доказательство:

2. Из ∆ABD = ∆DBC  AD = DC  ВD – медиана по определению.

3. Из ∆ABD = ∆DBC  AВD = СВD.  ВD – биссектриса по определению.

Билет № 7.

1. Определение, изображение, обозначение луча (полупрямой). Какие полупрямые называются дополнительными? Аксиома откладывания отрезков (формулировка, чертеж, символическая запись).

Определение 1. Точки прямой, лежащие по одну сторону от некоторой точки О этой прямой, вместе с точкой О образуют луч или полупрямую. Точку О называют началом луча.

Л учи обозначаются двумя большими буквами, первая из которых (О) указывает начало луча, а вторая – например B – произвольная точка на луче. Всякий луч имеет начало, но не имеет конца.

Определение 2. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными. OA и OB – дополнительные полупрямые.

Аксиома откладывания отрезков:

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и притом только один.

Дан отрезок АВ и луч ОС. Нужно отложить на луче ОС отрезок ON, равный отрезку АВ. Для этого измеряем отрезок АВ и откладываем от точки О отрезок ON.

NOC, ON = AB.