1. Дополнительное построение. Проведем отрезок bd – биссектрису авс.

2. ABD = DBC = (по св-ву биссектрисы).

4. Из ∆ABD = ∆DBC  A = C.

Теорема 2 (о свойстве углов равностороннего треугольника). Все углы равностороннего треугольника равны 60.

Д ано: ∆АВС; АВ = ВС = АС.

Доказать: А = В = С.

Доказательство:

1. АВ = ВС   АВС – равнобедренный  А = С (углы при основании равнобедренного треугольника).

2. АВ = АС   АВС – равнобедренный  В = С (углы при основании равнобедренного треугольника).

3. A = B = C.

4. По теореме о сумме внутренних углов треугольника A + B + C = 180.

3A = 180. A = B = C = 60.

Теорема 3 (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.

Д ано: ∆АВС; А = С. Доказать: АВ = ВС.

Доказательство:

Данная теорема является следствием теоремы о соотношениях между сторонами и углами в треугольнике.

Пусть в треугольнике два угла равны. Тогда равны и стороны, лежащие против этих углов. Действительно, если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны). Итак, если в треугольнике две стороны равны, то треугольник равнобедренный.

Теорема 4 (признак равностороннего треугольника). Если в треугольнике все углы равны, то он равносторонний.

Д ано: ∆АВС; А = В = С.

Доказать: АВ = ВС = АС.

Доказательство:

1. Пусть А = С  ∆АВС – равнобедренный  = ВС = АВ.

2. Пусть А = В  ∆АВС – равнобедренный  = ВС = АС.

3. АВ = ВС = АС.  ∆АВС – равносторонний.

2. Доказать теорему о свойствах углов, образованных при пересечении двух параллельных прямых секущей.

Теорема 1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

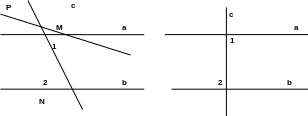
Дано: а II b; c – секущая. Доказать: 1 = 2.

Доказательство:

1) Допустим, что 1 2. Отложим от луча MN PMN =2 так, чтобы углы 2 и PMN были накрест лежащими углами при MP II b и секущей MN.

2) По построению PMN =2  РМ II b по признаку параллельности прямых.

3) Получено: через точку М проведены две прямые (а и РМ), параллельные прямой b, что невозможно, так как противоречит аксиоме параллельных прямых.

4) Допущение неверно. 1 = 2.

Следствие из теоремы 1. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Дано: а II b; c  а. Доказать: c  b.

Доказательство:

1) c  а  1 = 90.

2) c ∩ a  c ∩ b.

3) При пересечении образуются накрест лежащие углы  1 = 2.

4) Так как 1 = 90.  2 = 90.  c  b.

Теорема 2. Если две параллельные прямые пересечены секущей, то соответственные лежащие углы равны.

Дано: а II b; c – секущая. Доказать: 3 = 2.

Доказательство:

1) Так как a II b, то 1 =2 – внутренние накрест лежащие углы.

2) 1 =3 – вертикальные углы.

3) 3 = 2 – по аксиоме измерения углов как углы с равной градусной мерой.

Теорема 3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180.

Дано: а II b; c – секущая. Доказать: 4 + 2 =180.

Доказательство:

1) Так как a II b, то 1 =2 – внутренние накрест лежащие углы.

2) 1 + 4 = 180 – смежные углы.

3) 4 + 2 =180 – по аксиоме измерения углов как углы с равной градусной мерой.

Билет № 18.

1. Название углов, образованных при пересечении двух прямых третьей прямой. Сформулировать признаки параллельности прямых. Доказать признак параллельности по равенству соответственных углов.

Пусть имеются две прямые а и b, а также прямая с, пересекающая прямые а и b в точках А и В соответственно. Прямая с называется секущей по отношению к прямым а и b.

При пересечении двух прямых третьей (секущей) образуются пары углов:

1 и 4, 2 и 3, 5 и 8, 6 и 7 – вертикальные. Два угла, стороны одного из которых являются продолжениями сторон другого, называются вертикальными. Вертикальные углы равны.

1 и 2, 2 и 4, 1 и 3, 3 и 4, 5 и 6, 7 и 8, 6 и 8, 5 и 7 – смежные. Два угла, у которых одна сторона общая, а две других являются дополнительными лучами, называются смежными. Сумма смежных углов равна 180. Угол, смежный с прямым, - прямой.

1 и 8, 2 и 7, 3 и 6, 4 и 5 – накрест лежащие, причем углы 1 и 8, 2 и 7 – внешние накрест лежащие; 3 и 6, 4 и 5 – внутренние накрест лежащие.

1 и 5, 2 и 6, 3 и 7, 4 и 8 – соответственные.

1 и 7, 2 и 8, 3 и 5, 4 и 6 – односторонние; причем углы 1 и 7, 2 и 8 – внешние односторонние; 3 и 5, 4 и 6 – внутренние односторонние.

Признаки параллельности прямых.

1. Две прямые, перпендикулярные к третьей прямой, параллельны.

2. Две прямые, параллельные третьей прямой, параллельны.

3. Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

4. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

5. Если при пересечении двух прямых третьей односторонние углы в сумме составляют 180, то прямые параллельны.

Т еорема Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

Дано:

Доказать:

Доказательство:

1)

2) и являются внутренними накрест лежащими

2. Доказать теорему о сумме внутренних углов треугольника и следствия из нее.

Теорема о сумме углов треугольника: Сумма внутренних углов треугольника равна 180°.

Д ано: ∆АВС.

Доказать:

Доказательство:

1. Проведем

Следствие 1. У любого треугольника хотя бы два угла острые.

Допустим, что у треугольника один острый угол или вообще нет острых углов. Тогда у этого треугольника есть хотя бы два угла, каждый из которых не меньше 90, а сумма этих углов не меньше 180. Это невозможно, так как сумма углов треугольника равна 180.

Следствие 2. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы этих треугольников равны.

Допустим, что у треугольников АВС и МРТ соответственно равны углы: А = М, В = Р. Тогда С = 180 - (А + В), Т = 180 - (М + Р). Следовательно, С = Т.

Следствие 3. У прямоугольного треугольника сумма острых углов равна 90.

Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180 - 90 = 90.

Следствие 4. У равнобедренного прямоугольного треугольника острые углы имеют градусную меру 45.

Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180 - 90 = 90. Поскольку эти углы равны, то градусная мера каждого 90 : 2 = 45.

Следствие 5. У равностороннего треугольника все углы имеют градусную меру 60.

Так как у равностороннего треугольника все углы равны между собой, а их сумма равна 180, то градусная мера каждого угла равна 180 : 3 = 60.

Билет № 19.

1. Сформулировать и доказать признаки равенства прямоугольных треугольников.

1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).

2 . Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).

3. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

─ следствие из второго признака равенства треугольников.

4. Если катет и противолежащий острый угол одного треугольника соответственно равны катету и противолежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).

Доказывается аналогично предыдущей теореме ─ следствие из II признака равенства треугольников.

5. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.

Д оказательство:

1. Так как С = С₁, то треугольник АВС можно наложить на треугольник А₁В₁С₁ так, что вершина С совместится с вершиной С₁, а стороны СА и СВ наложатся соответственно на лучи СА₁ и СВ₁.

2. Так как СА = С₁А₁, то вершина А совместится с вершиной А₁. Остается доказать, что совместятся точки В и В₁.

3. Предположим, что точки В и В₁ не совместятся. Рассмотрим Δ А₁В₁В₂ – равнобедренный, так как АВ = A₁B₁  А₁В₂ = A₁B₁. Тогда A₁B₁В₂ = A₁В₂B₁. Заметим, что A₁B₁С₁ - острый угол прямоугольного треугольника А₁В₁С₁, а A₁B₁В₂, смежный с ним, - тупой. Поскольку в треугольнике не может быть двух тупых углов, то это невозможно. Значит, точки В и В₁ совместятся.