2. Суть метода наложения (суперпозиции) для расчета разветвленных электрических цепей.

Расчет сложной цепи методом наложения осуществляется следующим образом: поочередно находят токи в ветвях, создаваемые каждой ЭДС в отдельности, исключая действия остальных ЭДС из схемы, но оставляя в цепи их внутренние сопротивления. Действительные токи в ветвях находят путем векторного суммирования токов, создаваемых каждой ЭДС с учетом принятых условно-положительных направлений.

2. Суть метода контурных токов для расчета разветвленных электрических цепей.

Рассмотрим схему сложной электрической цепи, в трех независимых контурах которой содержится четыре ЭДС.

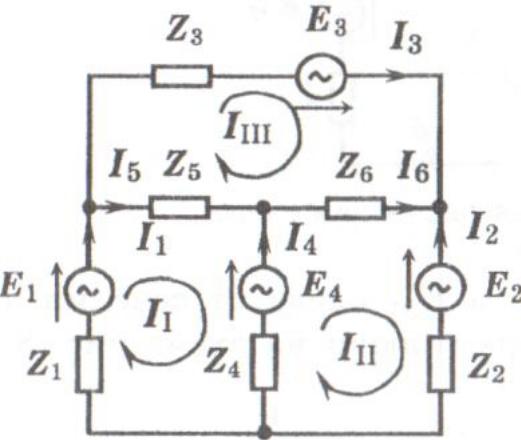
Схема содержит шесть ветвей, токи которых подлежат расчету. На рисунке показаны условно- положительные направления токов всех ветвей: I₁...I₆. Кроме того, на схеме показаны фиктивные токи трех контуров — так называемые контурные токи I_I, I_II, I_III, обтекающие свои контуры по часовой стрелке.

Поскольку реальные токи ветвей можно выразить через контурные токи, количество уравнений для искомых токов, подлежащих расчету, сокращается почти в два раза.

Установим связи между токами ветвей и контурными токами:

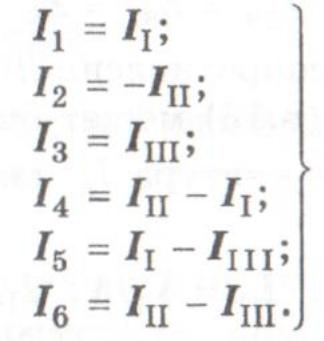
Запишем для трех контуров по второму закону Кирхгофа следующие уравнения:

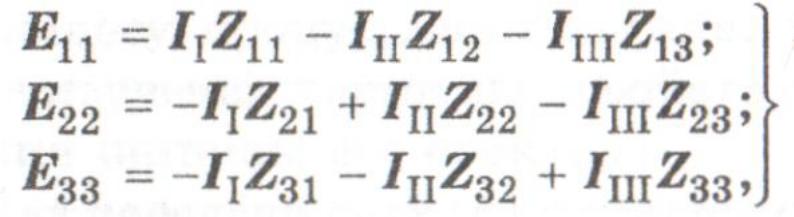
где

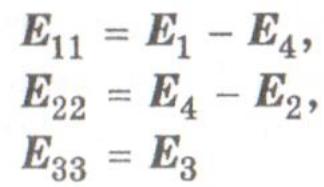
При этом сопротивления

являются собственными сопротивлениями контуров, а сопротивления

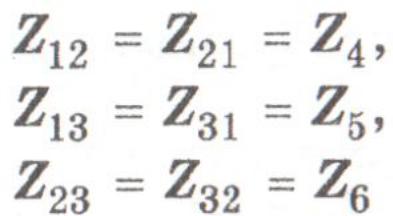
называют взаимными сопротивлениями контуров.

Система уравнений может быть разрешена методом определителей. Ток k-гo контура I_к находится как I_к = ∆ _k / ∆ , т.е.

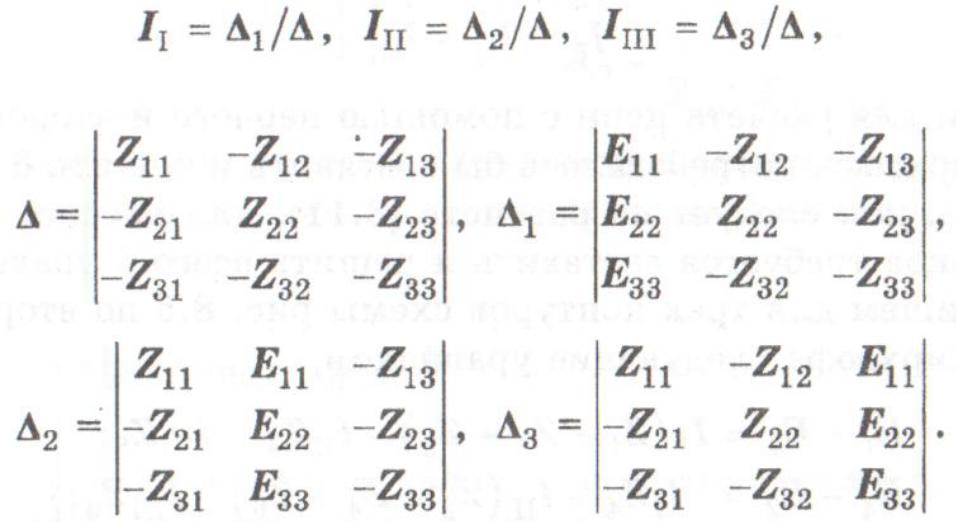
2. Суть символического метода при расчете линейных цепей гармонического тока.

Одним из наиболее распространенных режимов работы электрической цепи является режим работы при гармоническом воздействии. Это воздействие вызываются гармоническими источниками напряжения или тока и являются следствием возникновения токов в ветвях и разностей потенциалов между узлами цепи, которые можно считать откликами. В случае если цепь содержит только линейные элементы, то задачи отклика цепи решается символический метод (метод комплексных амплитуд).

Условия применимости символического метода: 1) электрическая цепь - линейная;

2) воздействие – гармоническое.

Задача решается только для установившегося режима работы цепи.

Основные положения символического метода:

1) связь между токами и напряжениями в линейных пассивных элементах электрических цепей R, L и C выражается линейными операторами;

2) применение линейных операторов к гармонической функции превращает ее в гармоническую функцию той же частоты;

3) гармоническая функция может быть заменена комплексным числом – своей комплексной амплитудой.

В связи с этим нахождение отклика цепи, являющегося гармонической функцией той же частоты, что и воздействие, можно свести к алгебраической задаче с применением аппарата комплексных чисел.

Расчет линейных электрических цепей символического метода (алгоритм символического метода):

1) гармоническое воздействие заменяется комплексным числом (прямой переход);

2) цепь представляется комплексной частотной функцией, то есть определяется нужная для решения задачи комплексная частотная функция цепи;

3) выполняется необходимые действия над представлениями воздействия и цепи в комплексной форме, в результате чего находится ответ в комплексной форме;

4) совершается переход от комплексной формы полученной величины к действующей форме (обратный переход).