Оценка качества полевых измерений

Показателями правильности измеренных углов (направлений) являются величины свободных членов условных уравнений. Подсчет свободных членов геометрических условий выполняется в процессе производства полевых работ по мере накопления материалов наблюдений, а перед началом уравнительных вычислений детально анализируются полевые вычисления.

Для подсчета свободных членов (невязок) треугольников составляется список треугольников (табл. 16). Для этого выписываются номера треугольников, название вершин и углы, вычисленные как разность направлений, приведенных к центрам знаков и редуцированных на плоскость. Далее замыкают треугольники (находят суммы углов) и вычисляют невязки треугольников ω. Предельные значения невязок треугольников не должны превышать величин, установленных инструкцией для соответствующего класса триангуляции.

Таблица 16 – Вычисление невязок треугольников

№ углов	Название вершин	Измеренные углы
		°	'	''
1	2	3	4	5
1	Сухой Лог	51	4	12,66
2	Зайцево	36	28	0,48
3	Бугры	92	27	46,08
	Σ	179	59	59,22
	ω1	0	0	-0,78
4	Бугры	88	22	50,67
5	Зайцево	37	35	6,88
6	Заря	54	2	4,1
	Σ	180	0	1,65
	ω2	0	0	1,65
7	Заря	48	32	8,83
26	Заря	45	53	26,6
8	Бугры	42	23	34,34
9	Сенной	43	10	48,61
	Σ	179	59	58,38
	ω3	0	0	-1,62
10	Сенной	100	41	38,17
11	Заря	47	42	16,2
12	Волчий	31	36	4,55
	Σ	179	59	58,92
	ω4	0	0	-1,08
13	Волчий	48	21	46,04
14	Сенной	84	24	25,36
15	Заячий	47	13	52,2
	Σ	180	0	3,6
	ω5	0	0	3,6
16	Заячий	54	59	4,01
17	Сенной	70	33	14,26
18	Дедово	54	27	41,1
	Σ	179	59	59,37
	ω6	0	0	-0,63

Продолжение таблицы 16

1	2	3	4	5
27	Дедово	29	45	46,47
19	Дедово	30	43	34
25	Дедово	38	10	47,07
20	Сенной	43	36	45,46
21	Сухой Лог	37	43	5,19
	Σ	179	59	58,18
	ω7	0	0	-1,82
22	Сухой Лог	25	41	2,98
23	Бугры	136	45	48,91
24	Сенной	17	33	8,15
	Σ	180	0	0,04
	ω8	0	0	0,04
9	Сенной	43	10	48,61
20	Сенной	43	36	45,46
24	Сенной	17	33	8,15
26	Заря	45	53	26,6
27	Дедово	29	45	46,47
	Σ	179	59	55,29
	ω9	0	0	-4,71

По невязкам треугольников вычисляется средняя квадратическая ошибка измерения угла по формуле Ферреро:

(10)

где ω – невязки в треугольниках;

n – количество треугольников в сети триангуляции.

Величина средней квадратической ошибки не должна превышать допуска – μ, установленного инструкцией.

m = 1,3 сек.

Затем подсчитывается общее число условных уравнений, считая измеренные углы, а не направления:

а) общее число уравнений без условий за жесткость вычисляется по формуле:

(11)

где N – число измеренных углов;

n – число всех пунктов в сети (жестких и определяемых);

б) число полюсных уравнений:

(12)

где р- число всех сторон сети (сплошных и несплошных);

в) число уравнений горизонта q равно количеству точек сети, вокруг которых измерены все углы;

г) число уравнений фигур

(13)

Д) число уравнений за жесткость

(14)

где R – число жестких элементов сети.

Тогда:

S = 27 – 16 + 4 = 15;

c = 17 – 16 + 3 = 4;

q = 2;

f = 15 – 2 – 4 = 9;

r = 6 – 4 = 2.

Для данной сети составлены следующие уравнения:

1. Уравнения фигур

(1) + (2) +(3) + ω1 = 0

(4) + (5) +(6) + ω2 = 0

(7) + (8) +(8) + (26) + ω3 = 0

(10) + (11) +(12) + ω4 = 0

(14) + (15) +(13) + ω5 = 0

(16) + (17) +(18) + ω6 = 0

(19) + (20) +(21) + (25) + (27) + ω7 = 0

(24) + (22) +(23) + ω8 = 0

(9) + (20) +(24) + (26) + (27) + ω9 = 0

3. Уравнения горизонта

(9) + (10) + (14) + (17) + (20) + (24) + ω10 = 0

(3) + (4) + (8) + (23) + ω11 = 0

4. Уравнения за жесткость:

а) суммы углов:

(1) + (22) + ω12 = 0

б) стороны:

5. Полюсные уравнения

Далее вычисляют свободные члены условных уравнений:

1. Для уравнений фигур свободные члены равны невязкам в треугольниках.

2.Вычисление свободного члена уравнения горизонта производится в табл.17.

3. Свободный член уравнения суммы углов вычисляется в табл.18 по формуле:

ω12 = (αСенной - Сухой Лог - αСухой Лог - Зайцево )-(1+22) (15)

4.Свободный член полюсного уравнения вычисляется в табл.20 по формуле:

(16)

где П1 и П2 - произведения синусов углов числителя и знаменателя.

При этом вычисляют допустимое значение свободного члена полюсного уравнения по формуле:

(17)

где β - углы, входящие в полюсное уравнение;

μ = 1,5 сек - средняя квадратическая ошибка измеренного угла, установленная инструкцией для соответствующего класса триангуляции.

5.Свободный член уравнения стороны вычисляется в табл.19 по формуле:

(18)

Допустимое значение свободного члена базисного уравнения вычисляется по формуле:

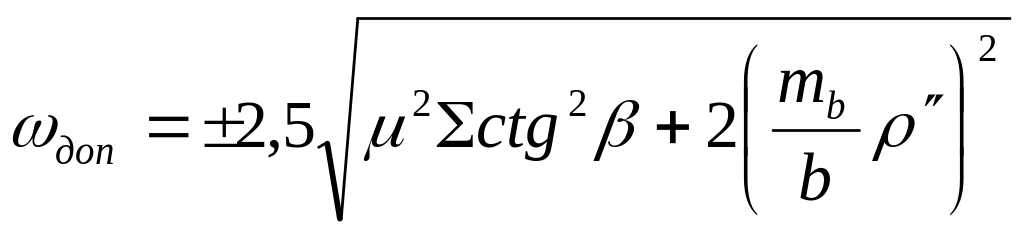(19)

где =1/300 000 (для 3-го класса триангуляции).

Таблица 17 – Вычисление свободных членов уравнений горизонта

№углов	Измеренные углы			№углов	Измеренные углы
	°	'	''		°	'	''
9	43	10	48,61	3	92	27	46,08
10	100	41	38,17	4	88	22	50,67
14	84	24	25,36	8	42	23	34,34
17	70	33	14,26	23	136	45	48,91
20	43	36	45,46
24	17	33	8,15
Σ	360	0	0	Σ	360	0	0
ω10	0	0	0	ω11	0	0	0

Таблица 18 – Вычисление свободного члена уравнения суммы углов

№углов	Измеренные углы
	°	'	''
1	51	4	12,66
22	25	41	2,98
Σ	76	45	15,64
α21	244	18	37,68
α23	167	33	23,5
α21-α23	76	45	14,18
ω12	0	0	1,46

Таблица 19 – Вычисление свободного члена уравнения стороны

№ углов	Измеренные углы			sinβ	ctgβ	ctg β	№ углов	Измеренные углы			sinβ	ctgβ	ctg β
	°	'	''					°	'	''
3	92	27	46,08	0,999076	-0,043	0,00185	2	36	28	0,48	0,594357	1,353	1,83078
24	17	33	8,15	0,301576	3,162	9,99531	23	136	45	48,91	0,68501	-1,064	1,13111
П1	0,301297078						П2	0,407140557
b1	8585,512		b2	6353,618				b2'		6353,554
ω13	-2,06
ωдоп	13,95

Таблица 20 - Вычисление свободных членов полюсных уравнений

№углов	Измеренные углы			sinβ	ctgβ	ctg2β	№углов	Измеренные углы			sinβ	ctgβ	ctg2β
	°	'	''					°	'	''
12	31	36	4,55	0,524004711	1,625	2,64191	11	47	42	16,2	0,739684	0,910	0,827711
15	47	13	52,2	0,734099357	0,925	0,85563	13	48	21	46,04	0,747367	0,889	0,790327
18	54	27	41,1	0,813724288	0,714	0,51024	16	54	59	4,01	0,818996	0,701	0,490857
26	45	53	26,6	0,718013609	0,969	0,93970	27	29	45	46,47	0,496412	1,749	3,05803
П1	0,22475015						П2	0,224752363
ω14	-2,03
ωдоп	11,93
2	36	28	0,48	0,594356883	1,353	1,830775	1	51	4	12,66	0,777916	0,808	0,652473
6	54	2	4,1	0,809370494	0,726	0,52653	5	37	35	6,88	0,609941	1,299	1,687969
19	30	43	34	0,510934707	1,682	2,830621	7	48	32	8,83	0,749369	0,884	0,780771
21+22	63	24	8,17	0,894171967	0,501	0,250714	25	38	10	47,07	0,618131	1,272	1,617216
П1	0,219776433						П2	0,219784412
ω15	-7,49
ωдоп	11,96
21+22	63	24	8,17	0,894171967	0,501	0,250714	20+24	61	9	53,61	0,876011	0,551	0,303108
24	17	33	8,15	0,301575634	3,162	9,995311	25	38	10	47,07	0,618131	1,272	1,617216
27+19	60	29	20,47	0,8702613	0,566	0,320385	22	25	41	2,98	0,43341	2,079	4,323561
П1	0,234675078						П2	0,234686869
ω16	-10,36
ωдоп	15,38
20+24	61	9	53,61	0,876011312	0,551	0,303108	27+19	60	29	20,47	0,870261	0,566	0,320385
26+7	94	25	35,43	0,997017151	-0,077	0,005992	9	43	10	48,61	0,684295	1,066	1,135569
19	30	43	34	0,510934707	1,682	2,830621	7	48	32	8,83	0,749369	0,884	0,780771
П1	0,446249506						П2	0,446260928
ω17	-5,28
ωдоп	8,70