6. Решения

1. Полагая в неравенстве треугольника , получим

2 ,

т.е. неотрицательность.

Также из неравенства треугольника при следует, что

.

И поскольку это неравенство справедливо при всех , то справедливо и неравенство

,

т.е. . Задача решена.

2. Для доказательства необходимо применить метод математической индукции и неравенство треугольника.

3. Все аксиомы выполнены, в частности, аксиома треугольника следует из свойств абсолютной величины.

Все аксиомы выполнены. Проверим аксиому треугольника:

.

Таким образом, в случаях и множество образует метрическое пространство.

Аксиома треугольника не имеет места. В самом деле

.

Следовательно, в случае множество не образует метрическое пространство.

4. Первые две аксиомы очевидны, проверим третью. На основе неравенства (1.8) и неравенства треугольника для метрики имеем

.

5. Да. Аксиома тождества является следствием строгой монотонности, аксиома симметрии очевидна. Докажем неравенство треугольника. Имеем

.

6. Докажем от противного. Пусть в некоторой окрестности и, следовательно, в некотором открытом шаре с центром в точке имеется лишь конечное число точек: . Положим . Тогда в открытом шаре уже нет точек из множества , что противоречит тому, что - предельная точка множества .

7. Если точка является предельной для множества , то она будет предельной и для , поскольку . Отсюда следует доказательство.

8. Пусть . Так как , , то из решения предыдущей задачи следует что . Докажем обратное включение. Пусть , но, например, . Тогда найдется окрестность точки такая, что . Далее возьмем произвольную окрестность точки . Можно считать, что ( иначе мы рассмотрим пересечение ). Так как , то должно быть . Следовательно, точка является точкой прикосновения множества , поэтому . Отсюда получается обратное включение.

9. Доказательство следует из свойства, выраженного в задаче 7 и того,

что замкнутый шар является замкнутым множеством.

Второй способ решения задачи. Пусть . Тогда существует последовательность такая, что . Отсюда получаем неравенство

.

Переходя здесь к пределу, получаем, что , т.е. . Задача решена.

9. Рассмотрим множество , в котором более одной точки и введем дискретную

метрику

Тогда для произвольного элемента имеем , но .

Отсюда следует, что . Задача решена.

9. Рассмотрим множество , состоящее из точек круга с обычной

евклидовой метрикой. Положим . В метрическом пространстве множество представляет собой шар радиуса 4, а само пространство - шар радиуса 3.

9. На плоскости рассмотрим замкнутые множества и

. Очевидно, что и в то же время . Задача решена.

9. Если , то для любого найдется такое , что при верно

неравенство . Это означает, что

,

так, что для всех и справедливо неравенство

.

Отсюда следует равномерная сходимость. Очевидно и обратное: из равномерной сходимости последовательности непрерывных функций к непрерывной функции следует сходимость в пространстве .

14. Пусть . Положим . Очевидно, что , поскольку, в противном случае нашлась бы по теореме Вейерштрасса такая точка , для которой . Аналогично доказывается неравенство .

Пусть . Тогда каждая функция , удовлетворяющая неравенству при всех , принадлежит множеству . Множество таких функций образует окрестность функции : . Таким образом, каждая функция принадлежит множеству вместе с некоторой своей окрестностью. Отсюда следует, что множество открыто. Задача решена.

15. Пусть - фундаментальная последовательность. Она сходится во всем пространстве , поскольку оно полно. И в силу замкнутости множества , предел последовательности принадлежит . Отсюда следует полнота .

Если - предельная мочка множества , то существует последовательность

, сходящая к . Далее сходящаяся последовательность является фундаментальной и в силу полноты множества сходится к некоторому элементу .

Поскольку предел единственен, то . Получили, что всякая предельная точка принадлежит множеству . Следовательно множество замкнуто.

16. Вначале докажем, что последовательность , является фундаментальной. Возьмем произвольное число . Поскольку , то существует номер такой, что при выполняется неравенство

.

Если , то

.

Таким образом, последовательность - фундаментальна. Покажем, что она не сходится. Пусть . Это означает, что

.

Отсюда следует, что , что невозможно. И доказана неполнота этого метрического пространства.

Отображение, которое всякому элементу ставит в соответствие изометрично отображает прямую с введенной метрикой на интервал с обычной евклидовой метрикой. Поэтому пополнение изометрично .

17. Аксиомы проверяются без труда, предлагаем провести самостоятельно. Далее , ,…, .

Очевидно, шары вложены друг в друга, и пересечение всех шаров представляет пустое множество.

Заметим, что в рассматриваемом пространстве расстояние между любыми двумя не равными элементами больше единицы. Отсюда следует, что всякая фундаментальная последовательность является постоянной, начиная с некоторого номера, и поэтому сходится.

18. Пусть дана фундаментальная последовательность . Тогда для любого найдется такой номер , что справедливо неравенство

, , . (5.1)

При любом фиксированном числовая последовательность также является фундаментальной и поэтому сходится. Обозначим предел через . А теперь перейдем к пределу в неравенстве (5.1), когда . В результате получим

, , .

Таким образом, доказали равномерную сходимость последовательности к функции . Осталось доказать непрерывность последней функции или принадлежность .

Для заданного найдем такое число , чтобы выполнялось неравенство

, .

А теперь, используя непрерывность функции , найдем такое , чтобы из неравенства следовало неравенство . В итоге при условии, что имеем

.

Следовательно, непрерывна. Задача полностью решена.

19. Очевидно, при . Далее имеем

, при .

Наибольшее значение мы нашли с помощью производной и затем использовали замечательный предел. Задача решена.

20. С учетом полноты пространства , достаточно доказать, что последовательность не является фундаментальной. Имеем

, .

Если здесь положить , то получим неравенство

.

Отсюда следует, что последовательность не является фундаментальной. Задача решена.

21. Заметим, что все аксиомы метрического пространства в данном случае выполняются. Далее приведем пример фундаментальной последовательности, которая не может сходиться к непрерывной функции. Возьмем последовательность

Полагая, что , найдем и оценим расстояния между элементами последовательности:

.

Отсюда следует фундаментальность данной последовательности. Далее докажем, что последовательность сходится по рассматриваемой метрике к разрывной функции

В самом деле

, при .

Пусть теперь - произвольная непрерывная функция. Используя неравенство треугольника, найдем

. (5.2)

Левое неравенство следует из непрерывности функции . Поскольку последнее слагаемое в правой части неравенства (5.2) стремится к нулю, а вся правая часть не может стремиться к нулю то, как следствие, не может последовательность сходиться к функции . Задача решена.

22. Пространство многочленов не полно, ибо в противном случае оно было бы замкнутым в пространстве . Согласно теореме Вейерштрасса (приложение 2) замыкание множества многочленов совпадает со всем пространством и в то же время есть непрерывные функции не являющиеся многочленами. Отсюда вытекает, что пространство многочленов не является полным. Задача решена.

23. Так как отличных от нуля чисел в определении последовательности конечное число, то . Далее докажем, что последовательность не является фундаментальной. В самом деле

.

24. Вначале заметим, что , поскольку метрика заимствована из пространства и все финитные последовательности принадлежат . Теперь покажем, что пространство не полно. Рассмотрим последовательность точек в пространстве . Эта последовательность является фундаментальной, поскольку

, при , .

Однако данная последовательность не имеет предела в . Докажем это от противного. Пусть и - финитная последовательность.

Для больших имеем

.

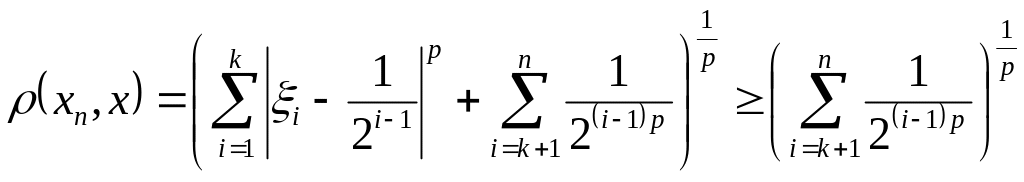С ростом расстояние , как следует из последнего неравенства, только растет и не может стремиться к нулю. Далее, несложно доказать, что пространство всюду плотно в пространстве , т.е. пополнение совпадает с пространством . Задача решена.

25. Пусть множество относительно компактно в полном метрическом пространстве . Возьмем произвольную последовательность и покажем, что она содержит сходящуюся в подпоследовательность. С этой целью построим последовательность такую, чтобы . В силу относительной компактности последовательность содержит фундаментальную подпоследовательность . Так как пространство полно, то сходится. Тогда и подпоследовательность также сходится, причем сходится к элементу множества , так как это множество замкнуто.

26. Рассмотрим последовательность точек из : , ,…. Имеем при . Поэтому последовательность и любая ее подпоследовательность не являются фундаментальными и тем более не сходятся. Задача решена.

27. Воспользуемся критерием относительной компактности, доказанным в теореме 4 третьей главы. Положим . Тогда и, следовательно, выполнено первое условие теоремы. Далее, так как сходится ряд для , то найдется такой номер , что . Тогда выполнено и второе условие теоремы . Задача решена.

28. Решение полностью повторяет решение задачи 27, если положить . Из сходимости этого ряда и условий задачи следует справедливость условий 4 третьей главы. Задача решена.

29. Рассмотрим последовательность функций , . Очевидно, эта последовательность принадлежит множеству . Далее, когда имеем

.

Такая последовательность не содержит фундаментальную подпоследовательность. Поэтому множество не является относительно компактным.

30. Проверим справедливость условий теоремы Арцела-Асколи. Каждую функцию из множества можно представить в виде

. (5.3)

Отсюда следует равномерная ограниченность: . Из (5.3) также следует:

.

С помощью этого неравенства несложно проверяется равностепенная непрерывность функций множества . Следовательно, выполнены условия теоремы Арцела-Асколи. Задача решена.

31. Достаточно доказать, что пересечение множества с произвольным шаром не пусто.

По условию задачи пересечение шара с множеством является непустым и открытым множеством. Поэтому существует шар такой, что . Точно также в открытом множестве выберем шар с условием, что . Далее в пересечении выберем шар , причем полагаем, что . Продолжая этот процесс, получим последовательность вложенных замкнутых шаров , радиусы которых стремятся к нулю. По теореме 3 из второй главы существует точка такая, что , при всех . Отсюда следует . Задача решена.

32. Нужно доказать, что произвольный шар в пространстве , содержит другой шар, свободный от точек множества .

Пусть и . Возьмем , тогда несложно поверить с помощью неравенства треугольника, что .

Введем точку и рассмотрим шар . С учетом того, что для точек имеем

.

Это означает, что

,

т.е. построенный шар содержится в исходном шаре . Осталось доказать, что в этом шаре нет точек из множества . С этой целью возьмем произвольную точку из множества и оценим расстояние до точки :

.

Таким образом, множество нигде не плотно в пространстве . Задача решена.

33. Вначале напомним, что канторово множество является пересечением множеств

,

причем множество является объединением отрезков, длина каждого из которых равна .

Теперь возьмем произвольную точку . Если - окрестность точки , то найдется такой интервал , для которого точка есть его центр и . Обозначим через тот отрезок множества , который содержит точку . При очень большом , очевидно, . Если обозначить через тот конец отрезка, который не совпадает с , то, как следует из построения канторова множества, . Следовательно, в каждой окрестности точки имеется другая точка канторова множества. Поэтому точка является предельной точкой. Задача решена.

34. Нужно доказать, что в произвольном интервале найдется другой интервал, в котором нет точек из канторова множества . Если в указанном интервале нет точек из , то задача решена. Предположим теперь, что имеется точка и . Как и в задаче 33 найдем такое большое натуральное число , чтобы и . Наконец, возьмем интервал длины с центром в середине . По построению, этот интервал не содержит точек из канторова множества и в тоже время содержится в интервале . Задача решена.

35. В пространстве рассмотрим подмножество , элементами которого

являются последовательности из 0 и 1. Как известно из курса математического анализа, таких последовательностей несчетное множество. Далее для любых , , очевидно, и поэтому . Пусть всюду плотное множество в . Тогда в каждом шаре , должен содержаться элемент , причем, если , то . Отсюда следует, что множество - несчетно. Задача решена.

35. Пусть множество нигде не плотно в метрическом пространстве , т.е.

замыкание не содержит ни одного открытого шара. Тогда дополнение пересекается с каждым шаром. Поэтому каждая точка метрического пространства является точкой прикосновения для множества и принадлежит его замыканию. Таким образом . Обратное утверждение, вообще говоря, неверно. Например, множество рациональных чисел всюду плотно на прямой с евклидовой метрикой, но дополнение – множество иррациональных чисел - также является всюду плотным множеством. Задача решена.

37. Пусть - открытое всюду плотное множество. Тогда дополнение является замкнутым множеством и поэтому совпадает со своим замыканием. Остается доказать, что не содержит ни одного шара. Предположим противное, пусть содержит некоторый шар . Этот шар не пересекается с множеством , поэтому точка не является точкой прикосновения для множества и не может принадлежать замыканию . А это противоречит тому, что множество всюду плотно. Это противоречие и доказывает, что не содержит ни одного шара, т.е. является нигде не плотным множеством. Задача решена.